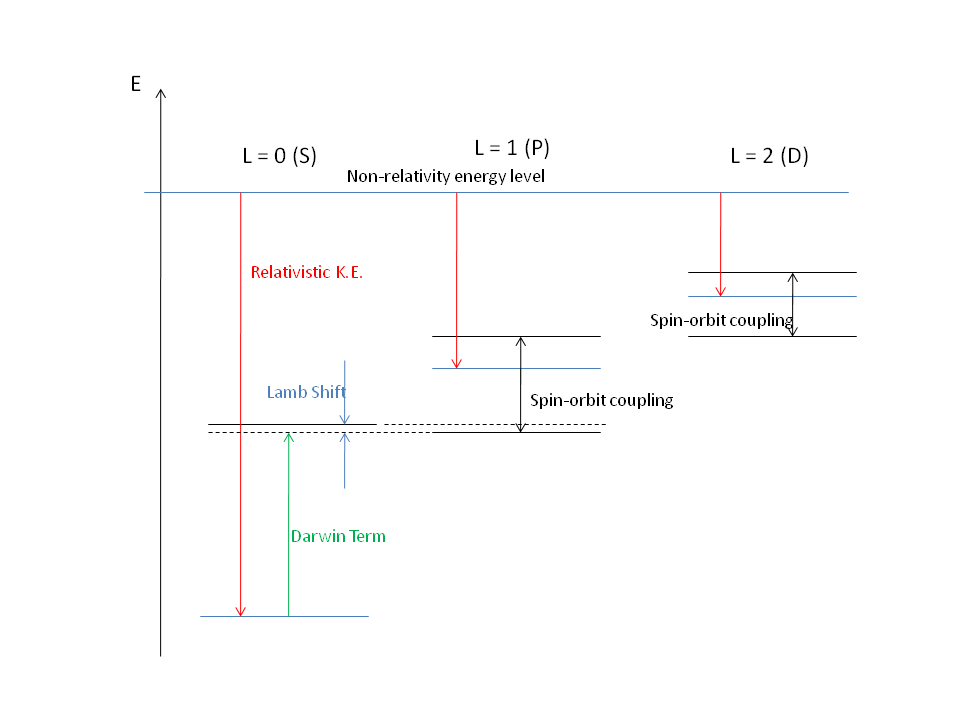
המבנה הדק
|
Read other articles:

Pour les articles homonymes, voir Isolation. Chambre insonorisée et anéchoïque ici utilisée par l'Organisation de consommateurs américaine Consumer Reports pour tester une paire d'écouteurs ; cette pièce est acoustiquement conçue pour empêcher toute réflexion significative du bruit sur les murs, le plafond et le sol On distingue parfois l'isolation acoustique, qui vise à éviter la propagation dans l'espace ou d'un lieu à l'autre de l'ensemble des bruits, de l'isolation phon...

Questa voce sull'argomento calciatori spagnoli è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Pere Pons Nazionalità Spagna Altezza 177 cm Peso 70 kg Calcio Ruolo Centrocampista Squadra AEK Larnaca Carriera Giovanili 2002-2012 Girona Squadre di club1 2012-2014 Girona19 (1)2014→ Olot14 (0)2014-2019 Girona179 (3)[1]2019-2022 Alavés79 (4)2022- AEK Lar...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Hungarian-American actress and socialite (1919–1995) The native form of this personal name is Gábor Éva. This article uses Western name order when mentioning individuals. Eva GaborGabor on the set of Green Acres in 1969BornÉva Gábor(1919-02-11)February 11, 1919Budapest, Hungarian RepublicDiedJuly 4, 1995(1995-07-04) (aged 76)Los Angeles, California, U.S.Resting placeWestwood Village Memorial Park CemeteryOther namesGábor ÉvaOccupationsActresssingersocialiteYears act...

此條目可参照外語維基百科相應條目来扩充。若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 Osagyefo克瓦米·恩克鲁玛第三届非洲联盟主席任期1965年10月21日—1966年2月24日前任贾迈勒·阿卜杜-纳赛尔继任约瑟夫·亚瑟·�...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Office for Foreign Relations and Information – news · newspapers · books · scholar · JSTOR (March 2011) (Learn how and when to remove this message) Office for Foreign Relations and InformationÚřad pro zahraniční styky a informaceSeal of ÚZSIHeadquarters of ÚZSI[1]Agency overviewFormedJanuary&...

Conservative advocacy organization This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (February 2020) (Learn how and when to remove this message) This article relies excessively on references to primary sources. Please improve thi...

German politician (1878–1929) Gustav StresemannPortrait of Stresemann (with visible Schmiss)Chancellor of Germany(Weimar Republic)In office13 August 1923 – 30 November 1923PresidentFriedrich EbertDeputyRobert SchmidtPreceded byWilhelm CunoSucceeded byWilhelm MarxMinister of Foreign AffairsIn office13 August 1923 – 3 October 1929ChancellorHimselfWilhelm MarxHans LutherHermann MüllerPreceded byHans von RosenbergSucceeded byJulius CurtiusChairman of the German People's P...

Silvano TrevisaniNazionalità Italia Calcio RuoloAla Termine carriera1959 - giocatore CarrieraGiovanili Scaligera Squadre di club1 1935-1938 Vigasio20 (6)1938-1940 Scaligera? (?)1940-1941 Audace SME? (?)[1]1941-1942 Verona8 (1)[2]1942-1943 Grion Pola22 (4)[1]1945-1947 Mantova59 (14)1947-1949 Genoa62 (9)1949-1951 SPAL71 (27)1951-1952 Fiorentina5 (0)1952-1953 Empoli32 (11)1953-1954→ Rosignano Solvay3 (0...

College ice hockey team season 1969–70 Cornell Big Red men's ice hockey seasonNational championECAC Holiday Tournament, championSyracuse Invitational, championECAC Hockey, championECAC Tournament, championNCAA tournament, champion Conference1st ECAC HockeyHome iceLynah RinkRecordOverall29–0–0Conference21–0–0Home12–0Road8–0Neutral9–0Coaches and captainsHead coachNed HarknessCaptain(s)Dick BertrandJohn HughesDan Lodboa[1]Cornell Big Red men's ice hockey seasons« 19...

KJ35 Alam Megah | LRT stationView of the station platform.General informationLocationJalan Beranang 27/14A Taman Bunga Negara Section 27, Alam Megah 40400, Shah Alam, SelangorMalaysiaOwned byPrasarana MalaysiaOperated byRapid RailLine(s)5 Kelana Jaya LinePlatforms2 Island platformsTracks2ConstructionStructure typeElevatedParkingAvailable with payment. 196 total parking bays.Other informationStation code KJ35 HistoryOpened30 June 2016Services Preceding station Following s...
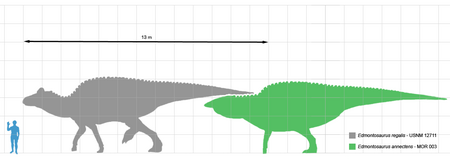
Edmontosaurus Periode Zaman Kapur Akhir, 73–66 jtyl PreЄ Є O S D C P T J K Pg N Kerangka E. regalis di Oxford University Museum of Natural HistoryTaksonomiFilumChordataKelasReptiliaOrdoOrnithischiaFamiliHadrosauridaeGenusEdmontosaurus Lambe, 1917 Tipe taksonomi†Edmontosaurus regalisLambe, 1917 Tata namaSinonim takson AnatosaurusLull & Wright, 1942 AnatotitanChapman & Brett-Surman, 1990 Claosaurus annectens Marsh, 1892 UgrunaalukMori et al., 2015[1] Spesies lain †E...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2019) عملة إسبانية تحمل صورة ملك إسبانيا الملك فرناندو السابع وقد نقش عليها اسم الحجاز وكانت تستخدم في الحجاز �...

Municipal Police officers in Rastro market, Madrid. Overall, rates of crime in Spain are relatively low in comparison to other European countries, with the notable exception of robberies.[1] In 2022 it was listed as number two out of 35 states in Europe with regard to the number of police-recorded robberies relative to population size,[1] although in 2020 it had a lower homicide rate than the European Union average.[2] Crime by type Theft Instances of robbery are part...

Foram assinalados vários problemas nesta página ou se(c)ção: As fontes não cobrem todo o texto. Necessita ser reciclada de acordo com o livro de estilo. Possui passagens que não respeitam o princípio da imparcialidade. SciVerse Scopus é um banco de dados de resumos e citações de artigos para jornais/revistas acadêmicos. Abrange cerca de 19,5 mil títulos de mais de 5.000 editoras internacionais, incluindo a cobertura de 16.500 revistas peer-reviewed nos campos científico, técnico...

Urban Transit AuthorityStatutory Authority overviewFormed1 July 1980; 44 years ago (1980-07-01)Preceding Statutory AuthorityPublic Transport CommissionDissolved15 January 1989; 35 years ago (1989-01-15)Superseding agencyState Transit AuthorityJurisdictionSydneyNewcastleHeadquartersSydneyKey documentTransport Authorities Act 1980 (NSW) The Urban Transit Authority, a former statutory authority of the Government of New South Wales, was responsible for the ope...

Evakuasi Prusia TimurBagian dari Perang Dunia IIPrusia Timur (merah)TanggalJanuari–Maret 1945LokasiPrusia TimurHasil Evakuasi lebih dari 1,8 juta penduduk Jerman [1]<Pihak terlibat Jerman Nazi Uni SovietTokoh dan pemimpin Gauleiter Erich Koch Ivan Chernyakhovsky Aleksandr Vasilevsky (komandan pasukan invasi Soviet)Korban 25.000–30.000[2][3][4][5] Evakuasi Prusia Timur adalah evakuasi warga dan personil militer Jerman dari wilayah Prusia Timur dan...

District of Vietnam Ninh Hải is a district (huyện) of Ninh Thuận province in the South Central Coast region of Vietnam. Geography It is located along the coast of northeastern Ninh Thuận, not far from (although not bordering) Cam Ranh in Khánh Hòa province. It borders the provincial capital, Phan Rang–Tháp Chàm, as well as Bác Ái district. Most of the district is mountainous, especially in the eastern part along the coast. The highest point is Chúa mountain (núi Chúa) at th...

TouvillecomuneTouville – Veduta LocalizzazioneStato Francia Regione Normandia Dipartimento Eure ArrondissementBernay CantonePont-Audemer TerritorioCoordinate49°18′15″N 0°45′36″E49°18′15″N, 0°45′36″E (Touville) Altitudine130 m s.l.m. Superficie3,47 km² Abitanti144[1] (2009) Densità41,5 ab./km² Altre informazioniCod. postale27290 Fuso orarioUTC+1 Codice INSEE27657 CartografiaTouville Modifica dati su Wikidata · Manuale Touvill...


















![{\displaystyle T=mc^{2}\left[1+{\frac {1}{2}}\left({\frac {p}{mc}}\right)^{2}-{\frac {1}{8}}\left({\frac {p}{mc}}\right)^{4}+O\left({\frac {p}{mc}}\right)^{6}\right]-mc^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce45bcd72b7e0e76a7e4f000746edd1379e4f88b)