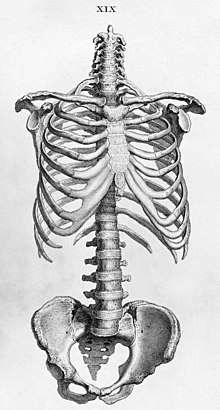
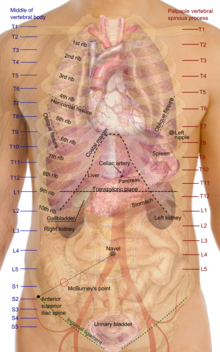
Tronc (anatomie)
|
Read other articles:

Perodua MyviInformasiProdusenPeroduaJuga disebutDaihatsu Sirion (Indonesia)[1]Masa produksiMei 2005 – SekarangBodi & rangkaKelasSubcompact/Supermini (B)Bentuk kerangka5-door hatchbackTata letakFront-engine, front-wheel-drive Perodua Myvi adalah mobil subkompak / supermini ( segmen-B ) yang diproduksi oleh pabrikan Malaysia Perodua sejak 2005. Berdasarkan Daihatsu Boon (juga bermerek Daihatsu Sirion, Toyota Passo, dan Subaru Justy ), Myvi adalah hasil kolaborasi Perodua...

Tebing Famara. Famara adalah sebuah gunungan (massif) di sisi utara Pulau Lanzarote, Kepulauan Canaria, Spanyol. Gunungan ini merupakan lereng timur sebuah gunung berapi yang meletus pada kala Miosen. Tebing Famara (Risco de Famara) merupakan sisa sebuah kaldera yang memiliki diameter 10 km dan berpusat di sebelah selatan Pulau La Graciosa.[1] Tebing Famara memiliki tinggi 671 m di Peñas del Chache [fr]. Di sebelah selatan tebing ini, terdapat sebuah pantai yang dis...

The Statement First UK edition (publ. Bloomsbury)AuthorBrian MooreGenreThriller novelPublisherBloomsbury (UK); E.P. Dutton (U.S.)Publication date1995 (UK); 1996 (U.S.)Preceded byLies of Silence (1990) Followed byThe Magician's Wife (1997) The Statement (1995) is a thriller novel by Northern Irish-Canadian writer Brian Moore. Set in the south of France and Paris in the early 1990s, The Statement is the tale of Pierre Brossard, a former officer in the pro-fascist militia t...

ماريك هامشيك (بالسلوفاكية: Marek Hamšík) هامشيك يلعب مع نابولي سنة 2016 معلومات شخصية الاسم الكامل ماريك هامشيك[1] الميلاد 27 يوليو 1987 (العمر 36 سنة)بانسكا بيستريتسا، تشيكوسلوفاكيا الطول 1.83 م (6 قدم 0 بوصة)[2] مركز اللعب وسط الجنسية سلوفاكي معلومات النادي النادي الحا�...

American shipping company (1848-1949) This article is about the shipping company chartered in New York state. For the shipping company in Washington, Oregon, California and Alaska, see Pacific Steamship Company. Pacific Mail Steamship CompanyIndustryTransportationFounded1848Defunct1949 (de jure), 1925 (de facto)Footnotes / referencesHouse Flag SS California, Pacific Mail's first ship The Pacific Mail Steamship Company was founded April 18, 1848, as a joint stock company under th...

Pour les articles homonymes, voir Haigneré. Claudie Haigneré(Claudie André-Deshays) Claudie Haigneré en 2014. Nationalité Française Sélection 2e groupe du CNES, 1985Corps européen des astronautes (ESA 1999) Naissance 13 mai 1957 (66 ans)Le Creusot, France Postes occupés Médecin, docteur en neurosciences SpationauteMinistre déléguée à la Recherche et aux Nouvelles technologiesMinistre déléguée aux Affaires européennes Occupation actuelle Ambassadrice et conse...

American novelist and playwright (1885–1968) Edna FerberFerber in 1928BornAugust 15, 1885 (1885-08-15)Kalamazoo, Michigan, U.S.DiedApril 16, 1968 (1968-04-17) (aged 82)New York City, U.S.OccupationNovelist, playwrightEducationLawrence UniversityGenreDrama, romanceNotable awardsPulitzer Prize for Fiction (1925) Edna Ferber (August 15, 1885 – April 16, 1968) was an American novelist, short story writer and playwright. Her novels include the Pulitzer Prize-winning So Big (1924...

American fantasy drama television series (1977–1984) This article is about the American television series that debuted in 1977. For other uses, see Fantasy Island (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fantasy Island – news · newspapers · books · scholar · JSTOR (August 2012) (Le...

VA-17 redirects here. The term may also refer to Virginia State Route 17. Virginia's 17th congressional districtObsolete districtCreated1793Eliminated1843Years active1793–1843 Virginia's 17th congressional district is an obsolete congressional district. It was eliminated in 1843 after the 1840 U.S. census. Its last congressman was Alexander H. H. Stuart. History Virginia's 17th congressional district was first formed in 1792. Although its initial geographic area was in northeastern Virgini...

Флаг гордости бисексуалов Бисексуальность Сексуальные ориентации Бисексуальность Пансексуальность Полисексуальность Моносексуальность Сексуальные идентичности Би-любопытство Гетерогибкость и гомогибкость Сексуальная текучесть Исследования Шк...

Bronze and later copper coin used in Ancient Rome Ases redirects here. For the acronym ASES, see American Solar Energy Society. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: As Roman coin – news · newspapers · books · scholar · JSTOR (November 2008) (Learn how and when to remove this message) c. ...

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапси...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...

American animated short series Whisker HavenAlso known asWhisker Haven Tales with the Palace PetsGenreAnimated seriesBased onPalace Pets toylineStory byShea FontanaDirected byAlan LauVoices of Emma Salzman Bailey Gambertogilo Myla Beau Sanai Victoria Natalie Coughlin Henry Kaufman Anne Halli Grace Kaufman Opening themeWhisker Haven ThemeCountry of originUnited StatesNo. of seasons3No. of episodes31ProductionRunning time31⁄2 minutes (seasons 1–2)2 minutes (season 3)Production companies...

Men at the 1990 Asian GamesVenueCapital Indoor StadiumDate23 September – 6 October 1990Nations11Medalists China Philippines South Korea← 19861994 → Basketball at the1990 Asian Gamesmenwomenvte Main article: Basketball at the 1990 Asian Games The 1990 Men's Asian Games Basketball Tournament was held in China from September 23, 1990, to October 6, 1990. Results Preliminary round Group A Pos Team Pld W L PF PA PD Pts Qualification 1...

Natural number ← 294 295 296 → ← 200 210 220 230 240 250 260 270 280 290 → List of numbersIntegers← 0 100 200 300 400 500 600 700 800 900 →Cardinaltwo hundred ninety-fiveOrdinal295th(two hundred ninety-fifth)Factorization5 × 59Divisors1, 5, 59, 295Greek numeralΣϞΕ´Roman numeralCCXCVBinary1001001112Ternary1012213Senary12116Octal4478Duodecimal20712Hexadecimal12716 295 is the natural number following 294 and preceding 296. In mathematics 295 is an odd composite number wi...

Wakil Bupati Gayo LuesPetahana(Jabatan Kosong)sejak 3 Oktober 2022Masa jabatan5 tahunDibentuk2007Pejabat pertamaFirdaus KarimSitus webwww.gayolueskab.go.id Berikut ini adalah daftar Wakil Bupati Gayo Lues dari masa ke masa. No Wakil Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Bupati Jabatan kosong 2002 2006 Ir. H.Muhammad Ali KasimMM(Penjabat) 2006 6 Maret 2007 dr. H.Aspino AbusamahM.Kes(Penjabat) 1 Letkol. Inf.Firdaus Karim 6 Maret 2007 26 November 2009 1 [Ket. 1] H.Ibnu Hasyim...
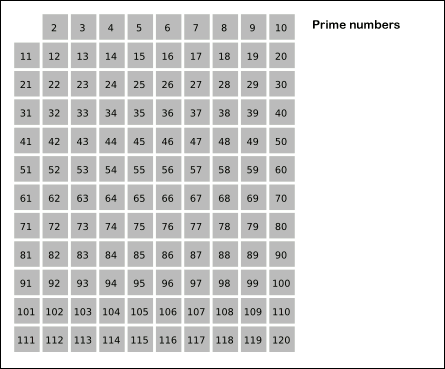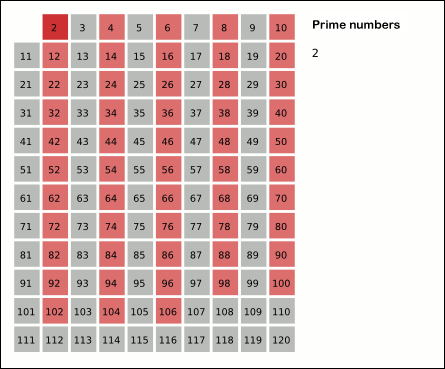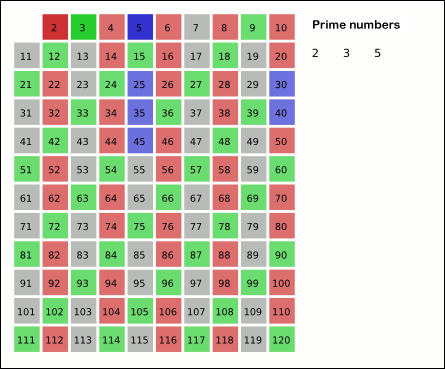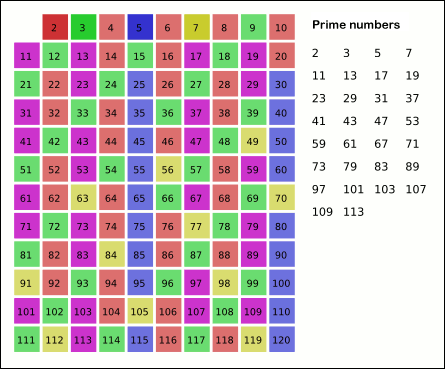
Ancient algorithm for generating prime numbers For the sculpture, see The Sieve of Eratosthenes (sculpture). Sieve of Eratosthenes: algorithm steps for primes below 121 (including optimization of starting from prime's square). In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of...

Penjahit di Hongkong sedang mengukur pakaian dari pemesannya Penjahit atau tailor adalah orang yang menjahit pakaian seperti kemeja, celana, rok, atau jas, untuk lelaki dan perempuan. Untuk melakukan pekerjaannya, penjahit perlu melakukannya dengan tangan atau dengan mesin jahit. Proses pengerjaan Desain Pakaian Tahap pertama adalah proses desain pakaian yang ingin dibuat. Pada tahap ini, penjahit dan pemesan akan berdiskusi bersama mengenai desain pakaian. Pemesan dapat mengajukan desainnya ...