Rick Flag

Page d’aide sur l’homonymie

Pour les articles homonymes, voir Flag.

Cet article est une ébauche concernant un personnage de fiction et les comics.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Rick Flag (parfois Rick Flagg) est le nom de plusieurs personnages de fiction de l'univers de DC Comics. Ils partagent tous un lien de parenté : père, fils et petit-fils.

Biographies fictives

Rick Flag

Richard Montgomery « Rick » Flag Senior dirige une unité appelée la Suicide Squadron durant la Seconde Guerre mondiale[1]. Durant sa première mission, il est l'unique survivant. Après la guerre, il épouse Sharon Race[2]. En 1951, à la suite de la disparition de la Société de justice d'Amérique et autres super-héros, le Président des États-Unis Harry S. Truman rappelle Flag, qui crée la Task Force X[3],[4].

L'unité Task Force X est faite de deux unités : une militaire ("Argent", dirigée par "Control") et une unité civile, la Suicide Squad avec des repris de justice[5].

Flag se sacrifie pour stopper un ancien ennemi de Blackhawk, War Wheel[3],[6].

Rick Flag Jr.

Rick Flag Jr.
Alias Richard Rogers Flag Junior
Famille Rick Flag III (fils), Richard Montgomery Flag (père), Sharon Race (mère)[7]
Affiliation Forgotten Heroes, Suicide Squad, Task Force X, United States Air Force[7]
Créé par Robert Kanigher
Ross Andru
Première apparition The Brave and the Bold #25 (septembre 1959)
Éditeurs DC Comics
modifier 

Le Capitaine Richard Rogers Flag Junior est le fils de Richard Flag. Il remplace son père dans l'équipe. Il y côtoie notamment sa petite-amie, Karin Grace, ainsi que le Dr. Hugh Evans et Jess Bright[8].

Rick Flag Jr. est chargé par le gouvernement de diriger la nouvelle Suicide Squad formée par Amanda Waller, ce qu'il accepte à contre-cœur. Immédiatement, Rick montre des signes d'instabilité et a du mal à gérer ces criminels, notamment Deadshot, qui est très différent de lui[3].

Rick Flag III

Rick Flag III est le fils de Rick Flag Jr. et Karin Grace.

Apparitions dans d'autres médias

Cinéma

Le personnage est interprété par Joel Kinnaman dans l'univers cinématographique DC.

Télévision

Rick Flag Jr. apparait dans un épisode de La Ligue des justiciers en 2005.

Entre 2010 et 2011, Rick Flag apparait sous les traits de Ted Whittall dans 4 épisodes de Smallville.

Jeu vidéo

En 2013, le personnage est présent dans le jeu vidéo Batman: Arkham Origins Blackgate.

Notes et références

  1. ↑ (en) John Ostrander (ill. Luke McDonnell), Secret Origins : The Secret Origin of the Suicide Squad, vol. 2, t. 14, DC Comics, , p. 6
  2. ↑ (en) John Ostrander (ill. Luke McDonnell), Secret Origins : The Secret Origin of the Suicide Squad, vol. 2, t. 14, DC Comics, , p. 7
  3. ↑ a b et c (en) Dan Wallace, The DC Comics Encyclopedia, New York, Dorling Kindersley, , 399 p. (ISBN 978-0-7566-4119-1 et 0-7566-4119-5), p. 128
  4. ↑ (en) John Ostrander (ill. Luke McDonnell), Secret Origins : The Secret Origin of the Suicide Squad, vol. 2, t. 14, DC Comics, , p. 7-9
  5. ↑ (en) John Ostrander (ill. Luke McDonnell), Secret Origins : The Secret Origin of the Suicide Squad, vol. 2, t. 14, DC Comics, , p. 8
  6. ↑ (en) John Ostrander (ill. Luke McDonnell), Secret Origins : The Secret Origin of the Suicide Squad, vol. 2, t. 14, DC Comics, , p. 14
  7. ↑ a et b (en) Richard Flag, Jr. (New Earth) - DC Comics Database
  8. ↑ (en) John Ostrander (ill. Luke McDonnell), Secret Origins : The Secret Origin of the Suicide Squad, vol. 2, t. 14, DC Comics, , p. 19

Liens externes

v · m
Créateurs
Membres
Adaptations à d'autres médias

Read other articles:

Ar-Rawabi

Ar-RawabiLingkunganNegaraArab SaudiProvinsiProvinsi MakkahPemerintahan • Wali kotaHani Abu Ras[1] • Gubernur kotaMish'al Al-SaudKetinggian12 m (39 ft)Zona waktuUTC+3 (AST) • Musim panas (DST)ASTKode pos(5 kode digit dimulai dari 23; e.g. 23434)Kode area telepon+966-12Situs webwww.jeddah.gov.sa/english/index.php Ar-Rawabi adalah sebuah permukiman padat penduduk di kota Jeddah di Provinsi Makkah, tepatnya di sebelah barat Arab Saudi.[3&#...

 

Diatessaron

Diatessaron dalam bahasa Arab dari abad ke-11 diterjemahkan oleh Abul Faraj Al Tayyeb Diatessaron adalah sebuah karya dari Tatianus sekitar tahun 150 atau 160.[1] Merupakan hasil upaya Tatianus yang mencoba membuat kumpulan keempat Injil menjadi sebuah cerita yang bersambung.[2] Diatessaron disebut juga “Harmoni Injil”.[2] Tatianus adalah seorang berasal dari Siria.[2] Fragmen Diatessaron milik Tatianus ini berhasil ditemukan di Dura-Europos, suatu daerah a...

 

Drochia

DrochiaKota BenderaLambang kebesaranNegara MoldovaDistrikDistrik DrochiaPendirian1777Pemerintahan • Wali kotaIgor Grozavu, sejak 2011Ketinggian741 ft (226 m)Populasi (2012) • Total20,400Zona waktuUTC+2 (EET) • Musim panas (DST)UTC+3 (EEST)Kode posMD-52xxKode area telepon+373 252 xx x xx Drochia adalah sebuah kota yang terletak di sebelah utara Moldova. Kota ini merupakan pusat administratif Distrik Drochia dan terletak 174,4 km sebe...

Teori semiotika Peirce

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Teori Semiotika Peirce merupakan ilmu atau metode analisis yang membahas mengenai sistem tanda yang diciptakan ahli filsafat asal Amerika bernama Charles Sanders Pierce yang terkenal dalam bidang logika terhadap manusia dan penalarannya. Peirce mengem...

 

Aldrichia ehrmanii

Aldrichia ehrmanii Aldrichia ehrmanii Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Diptera Famili: Bombyliidae Genus: Aldrichia Spesies: Aldrichia ehrmanii Aldrichia ehrmanii adalah spesies lalat yang berasal dari genus Aldrichia dan famili Bombyliidae. Lalat ini juga merupakan bagian dari ordo Diptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Lalat ini biasanya memakan nektar dan polen yang ada dalam bunga. Referensi Bisby F.A., Roskov Y.R., Orr...

 

Bromley and Sheppard's Colleges

Bromley and Sheppard's Colleges are located in Bromley and today provide accommodation for retired clergy and their dependents. Bromley College provides 40 self-contained dwellings, and Sheppard's College a further seven. Founded in the 17th century, with later additions and extensions, the property includes three listed buildings.[1][2][3] Bromley College Bromley College United Kingdom legislationBishop of Rochester's Charities Act 1670Act of ParliamentParliament of E...

1605 en France

Chronologie de la France ◄◄ 1601 1602 1603 1604 1605 1606 1607 1608 1609 ►► Chronologies Le Pont Neuf en 1618. Carte de Paris de Claes Jansz Visscher.Données clés 1602 1603 1604  1605  1606 1607 1608Décennies :1570 1580 1590  1600  1610 1620 1630Siècles :XVe XVIe  XVIIe  XVIIIe XIXeMillénaires :-Ier Ier  IIe  IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), Littératu...

 

NASA Distinguished Service Medal

This article is about NASA-awarded Distinguished Service Medal. For other U.S. versions, see Distinguished Service Medal (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: NASA Distinguished Service Medal – news · newspapers · books · scholar · JSTOR (November 2019) (Learn how and when to remo...

 

Seward Collins

American New York socialite and publisher Seward Collins from his 1917 The Hill School yearbook. Seward Bishop Collins (April 22, 1899 – December 8, 1952) was an American New York socialite and publisher. By the end of the 1920s, he was a self-described fascist. Biography Early life Collins was born in Albion, New York on April 22, 1899, to Irish Catholic parents. His father Herbert was involved early on in the development of United Cigar Stores, a chain that would eventually grow to ov...

Université d'Hawaï à Mānoa

Cet article est une ébauche concernant une université américaine et Hawaï. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Université d'Hawaï à MānoaHistoireFondation 1907StatutType Université publiqueDevise Ma luna a'e o na lahui a pau ke ola o ke kanaka., Above all nations is humanity.Membre de Asociación de Universidades de la Cuenca del Pacífico, Association of Public and Land-grant Universities (...

 

Saptahik Bartaman

Saptahik BartamanCompanyBartaman Pvt. Ltd.WebsiteOfficial website Saptahik Bartaman is a Bengali language weekly magazine published by Bartaman Pvt. Ltd. (the publisher of the newspaper Bartaman) from Kolkata, India. It had a circulation of 1,48,378, in January–June, 2011.[1] References ^ Breakup of circulation figures – town wise, district wise, state wise for the audit period January – June 2011 (XLS). India: Audit Bureau of Circulations. Retrieved 8 December 2011. ...

 

Jorge Antonio Serrano Elías

Questa voce sull'argomento politici guatemaltechi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Jorge Antonio Serrano ElíasRitratto ufficiale Presidente del GuatemalaDurata mandato14 gennaio 1991 –1º giugno 1993 Vice presidenteGustavo Adolfo Espina Salguero PredecessoreMarco Vinicio Cerezo Arévalo SuccessoreGustavo Espina Dati generaliPartito politicoMovimento di Azione e Solidarietà Firma Jorge Antonio Serrano Elías (...

Sonny Corleone

Fictional character from The Godfather series The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Sonny Corleone – news · newspapers · book...

 

Atlantic City (song)

1982 single by Bruce Springsteen Not to be confused with the 1948 song On the Boardwalk (In Atlantic City). Atlantic CitySingle by Bruce Springsteenfrom the album Nebraska B-sideMansion on the HillReleasedOctober 1982[1]RecordedJanuary 3, 1982StudioThrill Hill East, Colts Neck, New JerseyGenreFolk rockLength4:00Label Columbia (album) CBS 2794 (UK single) Songwriter(s)Bruce SpringsteenProducer(s)Bruce SpringsteenBruce Springsteen UK singles chronology Cadillac Ranch (1981) Atlantic...

 

Peripatric speciation

Speciation in which a new species is formed from an isolated smaller peripheral population Figure 1: Peripatric speciationFigure 2: Centrifugal speciationDiagrams representing the process of peripatric and centrifugal speciation. In peripatry, a small population becomes isolated on the periphery of the central population evolving reproductive isolation (blue) due to reduced gene flow. In centrifugal speciation, an original population (green) range expands and contracts, leaving an isolated fr...

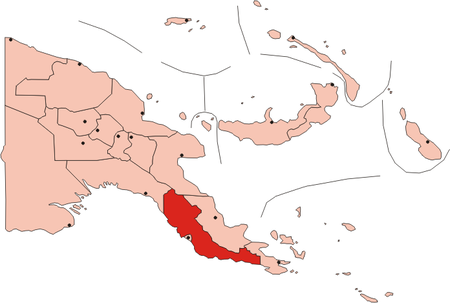
Provinsi Tengah, Papua Nugini

Artikel ini bukan mengenai Provinsi Papua Tengah. Koordinat: 9°30′S 147°40′E / 9.500°S 147.667°E / -9.500; 147.667 Provinsi Tengah Central ProvinceProvinsi BenderaCountry Papua New GuineaIbukotaBautamaPemerintahan • GubernurRufina PeterLuas • Total11,582 sq mi (29.998 km2)Populasi (2011) • Total269.756 • Kepadatan23/sq mi (9,0/km2)Zona waktuUTC+10 (AEST) Provinsi Tengah adalah sebuah ...

 

Supreme Court of Justice of Moldova

Supreme Court of Justice of MoldovaCurtea Supremă de Justiție a Republicii MoldovaHeadquarters in ChișinăuEstablished26 March 1996LocationChișinăuAuthorized byConstitution of MoldovaNumber of positions48LanguageRomanianWebsitecsj.mdPresidentCurrentlyAliona Miron (acting)Since27 March 2023 The Supreme Court of Justice of Moldova (Romanian: Curtea Supremă de Justiţie a Republicii Moldova) is the highest court in the Republic of Moldova that ensures the correct and uniform application of...

 

Begonia gunnerifolia

Begonia gunnerifolia TaksonomiSuperkerajaanEukaryotaKerajaanPlantaeDivisiTracheophytaOrdoCucurbitalesFamiliBegoniaceaeGenusBegoniaSpesiesBegonia gunnerifolia Linden dan André, 1875 Begonia gunnerifolia adalah spesies tumbuhan yang tergolong ke dalam famili Begoniaceae. Spesies ini juga merupakan bagian dari ordo Cucurbitales. Nama ilmiah spesies ini pertama kali diterbitkan oleh Jean Jules Linden dan Édouard André pada 1875. Referensi Pranala luar Begonia gunnerifolia pada situs web The Pl...

Emtmannsberg

Emtmannsberg Lambang kebesaranLetak Emtmannsberg di Bayreuth NegaraJermanNegara bagianBayernWilayahOberfrankenKreisBayreuthMunicipal assoc.Weidenberg Subdivisions20 OrtsteilePemerintahan • MayorThomas Kreil (CSU)Luas • Total22,31 km2 (861 sq mi)Ketinggian469 m (1,539 ft)Populasi (2013-12-31)[1] • Total1.051 • Kepadatan0,47/km2 (1,2/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos95517Kode area telepon09209P...

 

Golden triangle (mathematics)

Isosceles triangle in which the duplicated side is in the golden ratio to the base side A golden triangle. The ratio a/b is the golden ratio φ. The vertex angle is θ = 36 ∘ {\displaystyle \theta =36^{\circ }} . Base angles are 72° each. Golden gnomon, having side lengths 1, 1, and ϕ {\displaystyle \phi } A golden triangle, also called a sublime triangle,[1] is an isosceles triangle in which the duplicated side is in the golden ratio φ {\displaystyle \varp...