Programme de Hilbert
|
Read other articles:

Subprefecture and commune in Grand Est, FranceÉpernaySubprefecture and communeVineyards near Épernay Coat of armsLocation of Épernay ÉpernayShow map of FranceÉpernayShow map of Grand EstCoordinates: 49°02′25″N 3°57′36″E / 49.0403°N 3.96°E / 49.0403; 3.96CountryFranceRegionGrand EstDepartmentMarneArrondissementÉpernayCantonÉpernay-1 and 2IntercommunalityCA Épernay, Coteaux et Plaine de ChampagneGovernment • Mayor (2023–2026) Christ...

Duta Besar Indonesia untuk BahrainLambang Kementerian Luar Negeri Republik IndonesiaPetahanaArdi Hermawansejak 25 Oktober 2021KantorAl-Manamah, BahrainDitunjuk olehPresiden IndonesiaDibentuk29 Desember 2010Situs webkemlu.go.id/manama/id Berikut adalah daftar diplomat Indonesia yang pernah menjabat Duta Besar Republik Indonesia untuk Bahrain: No. Foto Nama Mulai menjabat Selesai menjabat Diangkat oleh Ref. 1 Chilman Arisman 3 September 2012(Kredensial: 19 Februari 2013) 2017 Susilo...

1953 aviation accident Air France Flight 152An Air France Lockheed L-749 Constellation similar to the accident aircraftAccidentDate3 August 1953 (1953-08-03)SummaryEngine detachment, ditchingSiteGulf of Fethiye, TurkeyMediterranean Sea 36°36′N 29°00′E / 36.6°N 29.0°E / 36.6; 29.0AircraftAircraft typeLockheed L-749A ConstellationOperatorAir FranceRegistrationF-BAZSFlight originParis-Orly Airport (ORY/LFPO)1st stopoverRoma-Ciampino Airport (CI...

Untuk aktris, lihat Kwon So-hyun (aktris). Ini adalah nama Korea; marganya adalah Kwon. Kwon So-hyunKwon So-hyun pada Mei 2015Nama asal권소현Lahir30 Agustus 1994 (umur 29)Seoul, Korea SelatanPekerjaan Penyanyi Pemeran Karier musikGenre K-pop Instrumen Vokal Tahun aktif2005–sekarangLabelCube Entertainment935 EntertainmentThe CNTArtis terkait 4Minute Chamsonyeo Nama KoreaHangul권소현 Alih AksaraGwon SohyeonMcCune–ReischauerKwŏn Sohyŏn Kwon So-hyun (lahir 30 Agustus 1994)&#...

Flüchtlingsandrang vor dem Notaufnahmelager Marienfelde in Berlin, Juli 1961 Flucht aus der Sowjetischen Besatzungszone und der DDR – im Sprachgebrauch der DDR „Republikflucht“ – war das Verlassen der DDR oder ihres Vorläufers, der Sowjetischen Besatzungszone (SBZ), oder Ost-Berlins ohne Genehmigung der Behörden. Von der Gründung der DDR am 7. Oktober 1949 bis in den Juni 1990 verließen über 3,8 Millionen Menschen den Staat, davon viele illegal und unter großer Gefahr...

Species of gastropod Phos lucubratonis Shells of Phos lucubratonis Scientific classification Kingdom: Animalia Phylum: Mollusca Class: Gastropoda (unranked): clade Caenogastropodaclade Hypsogastropodaclade Neogastropoda Superfamily: Buccinoidea Family: Nassariidae Genus: Phos Species: P. lucubratonis Binomial name Phos lucubratonis(Fraussen & Poppe, 2005)[1] Synonyms Antillophos lucubratonis Fraussen & Poppe, 2005 (original combination) Phos lucubratonis is a species of s...

Bagian dari Alkitab KristenPerjanjian LamaYosua 1:1 pada Kodeks Aleppo Taurat Kejadian Keluaran Imamat Bilangan Ulangan Sejarah Yosua Hakim-hakim Rut 1 Samuel 2 Samuel 1 Raja-raja 2 Raja-raja 1 Tawarikh 2 Tawarikh Ezra Nehemia Ester Puisi Ayub Mazmur Amsal Pengkhotbah Kidung Agung Kenabian Besar Yesaya Yeremia Ratapan Yehezkiel Daniel Kecil Hosea Yoël Amos Obaja Yunus Mikha Nahum Habakuk Zefanya Hagai Zakharia Maleakhi Deuterokanonika Tobit Yudit Tambahan Ester 1 Makabe 2 Makabe Kebijaksanaa...

Native American social activist and politician LaDonna HarrisLaDonna Harris (2011)BornLadonna Vita Tabbytite (1931-02-26) February 26, 1931 (age 93)Temple, Oklahoma, U.S.OccupationComanche social activistKnown forEasyRiders (June 1985 issue),first Native American woman to run for vice presidentPolitical partyDemocraticOther politicalaffiliationsCitizens (1980)Spouse Fred R. Harris (m. 1949; div. 1982)Children3 LaDonna Vita Tabbyti...

Badesi BadèsiKomuneComune di BadesiLokasi Austis di Provinsi NuoroNegaraItaliaWilayah SardiniaProvinsiSassari (SS)Pemerintahan • Wali kotaGiovanni Maria MamiaLuas • Total31,30 km2 (12,08 sq mi)Ketinggian102 m (335 ft)Populasi (2016) • Total1,849[1]Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos07030Kode area telepon079Situs webhttp://www.comunebadesi.ot.it Badesi (bahasa Sardinia: Badèsi) ada...

Geographical features of Moldova Geography of MoldovaContinentEuropeRegionEastern EuropeCoordinates47°N 29°E / 47°N 29°E / 47; 29AreaRanked 135th • Total33,843.5 km2 (13,067.0 sq mi) • Land98.6% • Water†%Coastline0.407 km (0.253 mi)BordersTotal land borders: Moldova–Ukraine border, Moldova–Romania borderHighest pointBălănești Hill428.9 mLowest point2 m (Dniester River) Satellite image of Mol...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

Gisele BündchenBündchen pada Januari 2015LahirGisele Caroline Bündchen[1]20 Juli 1980 (umur 43)Horizontina, Rio Grande do Sul, BrazilPekerjaan Model Aktris Aktivis Pebisnis Penulis Tahun aktif1997–kiniSuami/istriTom Brady (m. 2009)Anak2, dan 1 anak tiriInformasi modelingTinggi180 cm (5 ft 11 in)[2]Warna rambut Coklat[2] Warna mata Biru[2] ManajerIMG Models (Worldwide)[3]Model Management (Hamb...
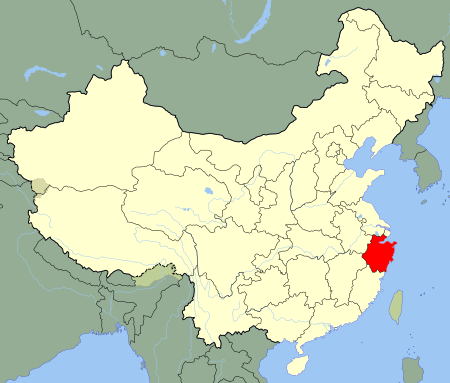
Городской округШаосинкит. упр. 绍兴, пиньинь Shàoxīng 30°00′00″ с. ш. 120°35′00″ в. д.HGЯO Страна Китай Провинция Чжэцзян История и география Площадь 8279,08 км² Часовой пояс UTC+8:00 Население Население ▲5 270 977 чел. (2020)[1] Цифровые идентификаторы Телефонный код...

European Track Championships Men's scratch at the 2022 UEC European Track ChampionshipsVenueMesse München, MunichDate13 AugustMedalists Iúri Leitão Portugal Moritz Malcharek Germany Roy Eefting Netherlands← 20212023 → 2022 UEC EuropeanTrack ChampionshipsSprintmenwomenTeam sprintmenwomenTeam pursuitmenwomenKeirinmenwomenOmniummenwomenMadisonmenwomenTime trialmenwomenIndividual pursuitmenwomenPoints racemenwomenSc...

Providing electrical power from shore to a shipThis article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Shore power – news · newspapers · books · scholar · JSTOR (June 2021) (Learn how and when to remove this message)Shore power or shore supply is the provision of shoreside electrical power to a ship at berth while i...

Public park in Brooklyn, New York Not to be confused with John Paul Jones Memorial Park in Kittery, Maine. Dover Patrol Naval War Memorial John Paul Jones Park is a public park located in Fort Hamilton, Bay Ridge, Brooklyn. The park borders Shore Road, Fourth Avenue, 101st Street, and Fort Hamilton Parkway. The park is managed by the New York City Department of Parks and Recreation, which acquired the property from the city of Brooklyn in 1897.[1] John Paul Jones Park is named after t...

زينب فواز معلومات شخصية الميلاد 1860تبنين الوفاة 1914(54 سنة)القاهرة مواطنة متصرفية جبل لبنان الزوج أديب نظمي الحياة العملية المهنة مؤرِّخة، وصحافية، وصاحب صالون أدبي، وروائية اللغات العربية أعمال بارزة الدر المنثور في طبقات ربات الخدور [ل�...

Ecorregión terrestre monte Paisaje típico de la ecorregión. Reserva Bosque Telteca, MendozaEcozona NeotropicalPaíses Argentina Ecorregiones – WWF[editar datos en Wikidata] La ecorregión terrestre monte (en inglés Argentine Monte) (NT0802) es una georregión ecológica situada en las sierras y llanuras del centro-oeste y noroeste de la Argentina. Se la incluye entre los pastizales, sabanas, y matorrales templados del neotrópico de la ecozona Neotropical.[1] Si b...
التسلسل الزمني جائحة فيروس كورونا 2019–20 في أبريل 2020معلومات عامةجزء من الخط الزمني لجائحة فيروس كورونا 2019-20 جانب من جوانب جائحة فيروس كورونا الموضوع الرئيس جائحة فيروس كوروناأبريل 2020 بتاريخ أبريل 2020 تاريخ البدء 1 أبريل 2020 تاريخ الانتهاء 30 أبريل 2020 التسلسل الزمني جائحة فيرو�...

Pho Khun Si Inthrathit Si Inthrathitศรีอินทราทิตย์Pho Khun Si InthrathitStatue of Si Inthrathit, Sawankhalok District, Sukhothai Province, ThailandPho Khun of SukhothaiReign1238 - 1270PredecessorMonarchy establishedSuccessorBan MueangBorn1188Mueang RatDied1270 (aged 81/82 years old)Sukhothai KingdomSpouseSueangIssueBan MueangRam Khamhaeng the GreatThree other childrenHousePhra Ruang Dynasty Si Inthrathit (Thai: ศรีอินทราทิตย์, pronounced...