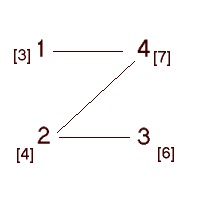
Problème du stable maximum
|
Read other articles:

ChimborazoTitik tertinggiKetinggian62.682 meter (205.650 ft) [note 1]Puncak4.123 mKoordinat01°28′09″S 78°49′03″W / 1.46917°S 78.81750°W / -1.46917; -78.81750 GeografiLetak EcuadorPegununganAndes, Cordillera OccidentalGeologiUsia batuanPaleogen[2]Jenis gunungStratovolcano Stratovolcano Chimborazo (diucapkan [tʃimboˈraso]) yang tidak aktif adalah puncak tertinggi Ekuador. Letusan terakhirnya diduga terjadi pada awal milenium ...

Franz von PapenPapen, 1933 Kanselir JermanMasa jabatan30 Mei 1932 – 17 November 1932PresidenPaul von Hindenburg PendahuluHeinrich BrüningPenggantiKurt von SchleicherDiplomat Jerman untuk TurkiMasa jabatanApril 1939 – Agustus 1944Dicalonkan olehAdolf Hitler PendahuluFriedrich von KellerPenggantiWilhelm Haas (1952)Diplomat Jerman untuk AustriaMasa jabatanAgustus 1934 – Februari 1938Dicalonkan olehAdolf Hitler PendahuluKurt RiethPenggantiCarl-Hermann Mueller-Gra...

Italian anatomist For the legendary Christian martyr known as Eustachius or Eustace, see Saint Eustace. Bartolomeo EustachioBornc. 1500–1510San SeverinoDied27 August 1574FossombroneNationalityItalianOther namesBartholom(a)eus EustachiusKnown forEustachian tube Eustachian valveScientific careerFieldsAnatomyNotable studentsVolcher Coiter Tabulae anatomicae (Rome, 1783): Table 21 Tabulae anatomicae (Rome, 1783): Title page Bartolomeo Eustachi (c. 1500–1510 –&...

Work stoppage caused by the mass refusal of employees to work Go on strike redirects here. For the song by Lower Than Atlantis, see Changing Tune. A trade union rally in Sydney, 2018 Part of a series onOrganized labor Labor movement Conflict theoriesDecent workExploitation of laborTimelineNew unionismProletariatSocial movement unionismSocial democracyDemocratic socialismSocialismCommunismSyndicalismUnion bustingAnarcho-syndicalismNational-syndicalism Labor rights Freedom of association Collec...

Surah ke-2الْبَقَرَة Al-BaqarahSapiTeks ArabTerjemahan KemenagKlasifikasiMadaniyahJuz1–3Jumlah ruku40Jumlah ayat286MuqaṭṭaʻātAlif, Lam, Mim← Al-FatihahAli Imran → Surah Al-Baqarah (Arab: سورة البقرة, translit: sūrah al-baqarah, lit. 'Sapi'code: ar is deprecated ) adalah surah ke-2 dalam Al-Qur'an, serta merupakan surah terpanjang.[1] Surah ini terdiri dari 286 ayat, 6.221 kata, dan 25.500 huruf dan tergolong surah M...

Strada statale 306Casolana RioleseLocalizzazioneStato Italia Regioni Emilia-Romagna Toscana Province Ravenna Firenze DatiClassificazioneStrada statale InizioCastel Bolognese FineMarradi Lunghezza48,389[1][2] km Provvedimento di istituzioneD.M. 14/04/1961 - G.U. 145 del 15/06/1961[3] GestoreTratte ANAS: nessuna (dal 2001 la gestione è passata alla Provincia di Ravenna ed alla Provincia di Firenze) Manuale La ex strada statale 306 Casolana Riole...

A type of ketchup or sauce with added curry powder, popular in West Europe Curry ketchupTypeKetchupMain ingredientsTomato paste, curry powder Media: Curry ketchup Curry ketchup, also called Currygewürzketchup (lit. curry spice ketchup) in Germany, is a spiced variant of ketchup and a common sauce in Belgium, Germany, Denmark and the Netherlands. It is typically served on prepared meats such as frikandel, or on French fries.[1] In Germany, it is the basis of the dish currywu...

Pour les articles homonymes, voir 3e régiment. 3e régiment de cuirassiers3e régiment de cavalerie Insigne régimentaire du 3e Régiment de Cuirassiers. Création 1635 Dissolution 1998 Pays France Branche armée de terre Type Régiment de Cuirassiers Rôle Cavalerie Fait partie de 8e Brigade Motorisée Garnison LyonReimsTrèvesAlgérie(1956-1963)SissonneLilleChenevières Devise Retrocedere Nescit(« Il ne sait pas reculer ») Inscriptionssur l’emblème Valmy 1792Maren...

Stadion AkademiMiniCOMS, MinihadNama lengkapStadion Akademi Manchester CityLokasiManchester, InggrisKoordinat53°28′52″N 2°11′34″W / 53.48111°N 2.19278°W / 53.48111; -2.19278Koordinat: 53°28′52″N 2°11′34″W / 53.48111°N 2.19278°W / 53.48111; -2.19278PemilikManchester City F.C.OperatorManchester City F.C.Kapasitas7.000[1]PermukaanRumputKonstruksiDibuka8 Desember 2014Biaya£200 juta (total nilai untuk fasilitas latiha...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Società Sportiva Dilettantistica Calcio Città di Castello. Unione Sportiva TifernoStagione 1939-1940Sport calcio Squadra Tiferno Allenatore Domenico Giacobbe Presidente Mario Tellarini Serie C5º posto nel girone G. 1938-1939 1940-1941 Si invita a seguire il mo...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

2023 television film by Anya Adams Prom PactOfficial release posterGenreRomantic comedyWritten byAnthony LombardoDirected byAnya AdamsStarring Peyton Elizabeth Lee Milo Manheim Blake Draper Monique Green Arica Himmel Jason Sakaki David S. Jung Wendi McLendon-Covey Margaret Cho Country of originUnited StatesOriginal languageEnglishProductionExecutive producers Julie Bowen Melvin Mar Jake Kasdan Rachael Field Anya Adams Running time98 minutesProduction companies Bowen and Sons The Detective Age...

American legislative district Pennsylvania's 100th StateHouse of RepresentativesdistrictRepresentative Bryan CutlerR–Fulton Township Demographics94.9% White1.9% Black3.6% HispanicPopulation (2011) • Citizens of voting age63,24846,342 The 100th Pennsylvania House of Representatives District is located in Southeastern Pennsylvania and has been represented since 2007 by Bryan Cutler. District profile The 100th Pennsylvania House of Representatives Dist...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) نقش تل القاضيمعلومات عامةتاريخ الاكتشاف 1993تعديل - تعديل مصدري - تعديل ويكي بيانات النقش معروض في متحف إسر...

List of events ← 1583 1582 1581 1580 1579 1584 in France → 1585 1586 1587 1588 1589 Decades: 1560s 1570s 1580s 1590s 1600s See also:Other events of 1584History of France • Timeline • Years Events from the year 1584 in France Incumbents Monarch – Henry III[1] Events 31 December – Treaty of Joinville Births Full date missing André Duchesne, historian and geographer (died 1640)[2] Mathieu Molé, statesman (died 1656) Deat...

Godowsky (1935; by Carl Van Vechten) Leopold Mordkhelovich Godowsky Sr. (13 Februari 1870 - 12 November 1938) adalah seorang pianis virtuoso, komponis, dan guru Amerika Serikat kelahiran Lituania. Ia adalah salah satu pianis yang dihormati di eranya[1]. Ia dijuluki sebagai Buddha Piano. Sebagai komposer, karya terkenalnya adalah Java Suite, Triakontameron, Passacaglia, dan Walzermasken, selain itu juga transkipsinya dari karya-karya komponis lain, seperti 53 Studies on Chopin's Étude...

Neighborhood of the Bronx in New York CityBelmontNeighborhood of the BronxArthur Avenue streetscapeLocation in New York CityCoordinates: 40°51′18″N 73°53′10″W / 40.855°N 73.886°W / 40.855; -73.886Country United StatesState New YorkCityNew York CityBoroughBronxCommunity DistrictThe Bronx 6[1]Area[2] • Total0.476 sq mi (1.23 km2)Population (2010)[2][3] • Total27,378 �...
Kolom Winogradsky awalnya Kolom Winogradsky setelah beberapa minggu Kolom Winogradsky adalah suatu miniatur ekosistem buatan untuk membiakkan mikrob yang menyerupai kondisi ekologis sebenarnya dengan menyediakan sumber bakteri jangka panjang untuk pengkayaan kultur.[1] Kolom Winogradsky adalah salah satu cara sederhana untuk mempelajari hubungan silang antara dua komponen suatu lingkungan alami di laboratorium.[1] Penemuan Kolom Winogradsky merupakan ide seorang ilmuwan Rusia ...

American composer (born 1937) Philip GlassGlass in 1993Background informationBorn (1937-01-31) January 31, 1937 (age 87)Baltimore, Maryland, U.S.GenresMinimalismcontemporary classicalfilm scoreOccupation(s)ComposerDiscographyList of compositionsYears active1964–presentMember ofPhilip Glass EnsembleWebsitephilipglass.comMusical artist Philip Glass (born January 31, 1937) is an American composer and pianist. He is widely regarded as one of the most influential composers of the late 20th ...

Zambian National Assembly constituency Politics of Zambia Constitution Human rights Government President Hakainde Hichilema Vice-President Mutale Nalumango Cabinet Legislature National Assembly Speaker: Nelly Mutti Constituencies Judiciary Constitutional Court President: Mulela Margaret Munalula Supreme Court Chief Justice: Mumba Malila Elections General 1964 1968 1973 1978 1983 1988 1991 1996 2001 2006 2011 2016 2021 Presidential 2008 2015 Referendums 1969 2016 Political parties By-elections...