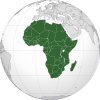
Politique en Guinée équatoriale

La Guinée équatoriale est une république à régime présidentiel où le président de la République est le chef de l'État et le Premier ministre le chef du gouvernement.

Pouvoir exécutif

Palais présidentiel de Guinée équatoriale à Malabo

Le président de la République est élu au suffrage universel pour un mandat de sept ans. La constitution de 1982 lui accorde de larges pouvoirs; il peut ainsi nommer et renvoyer les ministres, modifier des lois ou en introduire de nouvelles par décret et dissoudre le parlement.

Le Premier ministre est nommé par le président de la République. Il coordonne les activités du gouvernement, sauf dans les domaines des affaires étrangères, de la défense nationale et de la sécurité.

Pouvoir législatif

Le parlement (chambre des représentants du peuple) est jusqu'en 2013 monocaméral, comptant 100 membres élus pour cinq ans à la proportionnelle dans des circonscriptions à sièges multiples.

Depuis 2013, le parlement est bicaméral. Il est composé de la Chambre des députés et du Sénat.

Partis politiques et élections

La Guinée équatoriale est un État multipartite depuis 1991, où le Parti démocratique de Guinée équatoriale détient le pouvoir. D’autres formations mineures sont autorisées, mais à la condition de reconnaître la seule autorité du PDGE.

Élection présidentielle

Teodoro Obiang Nguema Mbasogo remporta l’élection présidentielle du 24 avril 2016 avec 93,53 % des voix.

Résultats de l'élection présidentielle équatoguinéenne de 2016[1]
Candidat Parti Voix %
Teodoro Obiang Nguema Mbasogo Parti démocratique de Guinée équatoriale 271 177 93,53
Avelino Mocache Mehenga Union de centre droit 4 556 1,57
Buenaventura Monsuy Asumu Coalition social démocrate 4 417 1,53
Benedicto Obian Mangue Indépendant 2 802 0,97
Carmelo Mba Bakalé Action populaire 2 415 0,83
Agustín Masoko Abegue Indépendant 2 412 0,83
Tomás Mba Monabang Indépendant 2 154 0,74
Votes valides 289 933 96,07
Votes blancs ou invalides 11 864 3,93
Total 301 797 100
Abstention 23 751 7,30
Inscrits/Participation 325 548 92,70

Élections législatives

Résultats des législatives équatoguinéennes de 2017
Partis Voix % Députés +/- Sénateurs +/-
Parti démocratique de Guinée équatoriale (PDGE) 250 260 92,00 99 en stagnation 55 en augmentation 1
Citoyens pour l'innovation (CI) 15 696 5,77 1 Nv 0 Nv
Convergence pour la démocratie sociale (CPDS) 6 066 2,23 0 en diminution 1 0 en diminution 1
Membres nommés[N 1] 15 en stagnation
Votes valides 272 022 99,46
Votes blancs 576 0,21
Votes invalides 904 0,33
Total 273 502 100 100 en stagnation 70 en stagnation
Abstentions 52 053 15,99
Nombre d'inscrits / participation 325 555 84,01

Pouvoir judiciaire

La Cour suprême est la plus haute instance judiciaire du pays. Ses juges sont nommés par le Président. Aux instances inférieures se trouvent les cours d’appel et les tribunaux locaux.

Le droit coutumier tient une place importante, lorsqu’il n’entre pas en conflit avec la loi écrite. Le système judiciaire combine des éléments de justice civile, traditionnelle et militaire et ne dispose pas de cadre procédural clair.

Notes

  1. ↑ Tous PDGE

Références

  1. ↑ Gouvernement

Compléments

Articles connexes

Liens externes

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Sur les autres projets Wikimedia :

v · m
v · m
Politique en Afrique
États souverains

Read other articles:

Festival Yosakoi

Penari Yosakoi di Harajuku, Tokyo. Festival Yosakoi (よさこい祭りcode: ja is deprecated , Yosakoi Matsuri) adalah festival tari Yosakoi yang diadakan setiap tahunnya di kota Kochi, Prefektur Kochi pada 9 Agustus hingga 12 Agustus. Festival berlangsung selama 4 hari, dengan puncak pentas utama pada 10 Agustus dan 11 Agustus. Malam sebelum pentas utama (9 Agustus) dimeriahkan oleh pesta kembang api, dan 12 Agustus adalah hari kompetisi nasional. Yosakoi adalah tari dengan ciri khas geraka...

 

Organisasi Kerja Sama Islam

Organisasi Kerja Sama Islamمنظمة التعاون الاسلاميOrganization of Islamic CooperationOrganisation de la coopération islamique BenderaSemboyan: Untuk menjaga kepentingan dan menjamin kemajuan dan kesejahteraan umat Islam  Negara anggota  Negara pengamat   Negara yang dihalangi keanggotaannyaPusat administrasi Jeddah, Arab SaudiBahasa resmiArabInggrisPrancisTipeOrganisasi antarpemerintahKeanggotaan57 negara anggotaPemimpin• Sekretari...

 

Mers intérieures de la côte ouest de l'Écosse

Carte de localisation des mers intérieures de la côte ouest de l'Écosse. Carte des Hébrides extérieures et intérieures et des mers intérieures. Les mers intérieures de la côte ouest de l’Écosse sont une aire maritime désignée ainsi par l’Organisation hydrographique internationale (OHI). Elle représente l’ensemble de l’espace maritime compris entre la terre ferme de l’Écosse, les Hébrides extérieures et la côte de l’Irlande septentrionale. Cet espace maritime inclu...

Statistiche della Serie A

Voce principale: Serie A. Questa voce raccoglie statistiche e record significativi del campionato italiano di calcio di Serie A dalla stagione 1929-1930. Questa lista è suscettibile di variazioni e potrebbe essere incompleta o non aggiornata. Indice 1 Evoluzione del campionato di Serie A a girone unico 1.1 Campionati disputati 2 Squadre partecipanti 2.1 Attuale 2.2 Storico 2.2.1 Partecipazioni, debutto, ultima partecipazione e stato attuale delle società 2.2.2 Partecipazioni per regione 2....

 

العلاقات الأسترالية الغواتيمالية

العلاقات الأسترالية الغواتيمالية أستراليا غواتيمالا   أستراليا   غواتيمالا تعديل مصدري - تعديل   العلاقات الأسترالية الغواتيمالية هي العلاقات الثنائية التي تجمع بين أستراليا وغواتيمالا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجع...

 

Słupsk Voivodeship

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Słupsk Voivodeship – news · newspapers · books · scholar · JSTOR (November 2009) (Learn how and when to remove this template message) Słupsk Voivodeship Słupsk Voivodeship (Polish: województwo słupskie) was a unit of administrative division and local gover...

South Hwanghae Province

Province of North Korea Hwangnam redirects here. For the district of Gyeongju, South Korea, see Hwangnam-dong. Province in Haeso, North KoreaSouth Hwanghae Province 황해남도ProvinceKorean transcription(s) • Chosŏn'gŭl황해남도 • Hancha黃海南道 • McCune-ReischauerHwanghaenam-do • Revised RomanizationHwanghaenam-doCountry North KoreaRegionHaesoCapitalHaejuSubdivisions1 cities; 19 countiesGovernment • Party C...

 

City of Lismore

Local government area in New South Wales, Australia This article is about the local government area. For the Australian regional city, see Lismore, New South Wales. Lismore CityNew South WalesLocation in New South WalesCoordinates28°49′S 153°17′E / 28.817°S 153.283°E / -28.817; 153.283Population44,334 (LGA 2021)[1]Established1879 (municipality):9 September 1946 (1946-09-09) (city)[2]Area1,290 km2 (498.1 sq mi)[3...

 

神山前进统一机构

  提示：此条目页的主题不是沙巴民族统一机构。   提示：此条目页的主题不是卡达山杜顺人统一机构 (1961)。 此條目可参照英語維基百科相應條目来扩充。若您熟悉来源语言和主题，请协助参考外语维基百科扩充条目。请勿直接提交机械翻译，也不要翻译不可靠、低品质内容。依版权协议，译文需在编辑摘要注明来源，或于讨论页顶部标记{{Translated page}}标签�...

Keluarga Cemara 2

Keluarga Cemara 2Poster rilis teatrikalSutradaraIsmail BasbethProduserAnggia KharismaDitulis olehM. Irfan RamliPemeran Ringgo Agus Rahman Nirina Zubir Adhisty Zara Widuri Putri Niloufer Bahalwan Penata musikOfel Obaja SetiawanSinematograferYadi SugandiPenyuntingHendra Adhi SusantoPerusahaanproduksi Visinema Pictures Jagartha Blibli Astro Shaw Tanggal rilis 9 Juni 2022 (2022-06-09) (Festival Film Internasional Balinale) 23 Juni 2022 (2022-06-23) (Indonesia) Durasi114 me...

 

Đại học Quốc gia Thành phố Hồ Chí Minh

Đại học Quốc giaThành phố Hồ Chí MinhNhà Điều Hành của Đại học Quốc gia Thành phố Hồ Chí Minh tại Thành phố Thủ Đức, Thành phố Hồ Chí MinhĐịa chỉThành phố Thủ Đức, Thành phố Hồ Chí Minh và Thành phố Dĩ An, tỉnh Bình Dương, Việt NamTọa độ10°52′07″B 106°47′47″Đ / 10,868562°B 106,796312°Đ / 10.868562; 106.796312Thông tinLoạiHệ thống đại học trọng điểm của ...

 

1876–77 United States House of Representatives elections

House elections for the 45th U.S. Congress 1876–77 United States House of Representatives elections ← 1874 & 1875 June 5, 1876 – March 1877[a][b] 1878 & 1879 → All 293 seats in the United States House of Representatives147 seats needed for a majority   Majority party Minority party   Leader Samuel J. Randall James A. Garfield Party Democratic Republican Leader's seat Pennsylvania 3rd Ohio 19th Last election 180 se...

Cairo (comics)

CairoDate2007PublisherVertigoCreative teamWritersG. Willow WilsonArtistsM. K. PerkerLetterersTravis LanhamEditorsJoan HiltyOriginal publicationDate of publicationNovember 7, 2007ISBN1-40121-734-6 Cairo is the first graphic novel of G. Willow Wilson with art by M.K. Perker, and published by the Vertigo imprint of DC Comics.[1] Synopsis The story is set in contemporary Cairo, and follows six characters as they are drawn into the intrigue surrounding a stolen hookah, a box containin...

 

الاتفاقية التركية للإصلاح الهيكلي

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2018) الاتفاقية التركية للإصلاح الهيكلي العام أو اتفاقية الإصلاح الهيكلي في تركيا 2000، هي اتفاقية وقعها صندوق النقد الدولي مع تركيا في 5 ديسمبر 2000، على شكل حزمة مس...

 

Japanese destroyer Harusame (1935)

Destroyer of the Imperial Japanese Navy For other ships with the same name, see Japanese destroyer Harusame. Harusame underway on 30 November 1943. History Empire of Japan NameHarusame Namesake春雨 (Spring Rain)[1] Ordered1931 FY BuilderMaizuru Naval Arsenal Laid down3 February 1935 Launched21 September 1935 Commissioned26 August 1937 Stricken10 August 1944 FateSunk by American bombers off New Guinea, 8 June 1944 General characteristics Class and typeShiratsuyu-class destroyer Displ...

ケイアイエレガント

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方）出典検索?: ケイアイエレガント – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2015年6月) ケイアイエレガント 2014年5月18日 東京�...

 

Примитивная почтовая марка

Оранжевый Маврикий (1847) Красный пенни (Великобритания, 1841) Церера[фр.] на марке Корриентеса (Аргентина, 1856) Церера[англ.] (Франция, 1849) Примити́вная почто́вая ма́рка (англ. «primitives» или «natives») — почтовая марка, разработанная и напечатанная с использованием заметно боле�...

 

2015 AFF Futsal Championship

2015 AFF Futsal ChampionshipTournament detailsHost country ThailandCityBangkokDates8–16 OctoberTeams10 (from 1 confederation)Venue(s)1 (in 1 host city)Final positionsChampions Thailand (11th title)Runners-up AustraliaThird place MalaysiaFourth place VietnamTournament statisticsMatches played24Goals scored251 (10.46 per match)Attendance61,800 (2,575 per match)Top scorer(s) Daniel Fogarty Jetsada Chudech (each 12 goals)← 2014 2016 →...

NGC 1883

NGC 1883 L'amas ouvert NGC 1883 Données d’observation(Époque J2000.0) Constellation Cocher[1] Ascension droite (α) 05h 25m 54,2s[2] Déclinaison (δ) 46° 29′ 25″ [2] Magnitude apparente (V) 12,0[3] Dimensions apparentes (V) 5,0′[3] Localisation dans la constellation : Cocher Astrométrie Distance environ 4 800 pc (∼15 700 al) [4] Caractéristiques physiques Type d'objet Amas ouvert Classe II1p[3] Galaxie hôte Voie l...

 

Löwenheim–Skolem theorem

Existence and cardinality of models of logical theories In mathematical logic, the Löwenheim–Skolem theorem is a theorem on the existence and cardinality of models, named after Leopold Löwenheim and Thoralf Skolem. The precise formulation is given below. It implies that if a countable first-order theory has an infinite model, then for every infinite cardinal number κ it has a model of size κ, and that no first-order theory with an infinite model can have a unique model up to isomorphism...