Partition d'un ensemble
|
Read other articles:
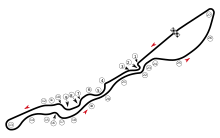
Grand Prix Arab SaudiSirkuit Corniche Jeddah (2021–sekarang)Informasi lombaJumlah gelaran3Pertama digelar2021Terbanyak menang (pembalap) Lewis Hamilton, Max Verstappen, dan Sergio Perez (1)Terbanyak menang (konstruktor) Red Bull Racing (2)Panjang sirkuit6.174 km (3.836 mi)Jarak tempuh308.450 km (191.662 mi)Lap50Balapan terakhir (2023)Pole position Sergio PerezRed Bull Racing-Honda RBPT1:28.265Podium 1. S. PérezRed Bull Racing-Honda RBPT1:21:14.894 2. M. VerstappenRed B...

Taman Nasional GlacierIUCN Kategori II (Taman Nasional)Kambing gunung, fauna khas Taman Nasional Glacier, di atas Hidden Lake Lokasi Taman Nasional Glacier di Amérika SarikatLetakFlathead County dan Glacier County, Montana, Amerika SerikatKota terdekatColumbia Falls, MontanaLuas1.013.322 acres[convert: unit tak dikenal]Didirikan11 Mei 1910Pengunjung2.965.309 (tahun 2018)Pihak pengelolaNational Park ServiceSitus webSitus web resmi Situs Warisan Dunia UNESCOBagian dariTaman Perdamaian Int...

Aku Ingin Menciummu Sekali SajaSutradaraGarin NugrohoProduserAnastasia RinaSkenarioGarin NugrohoNana MulyanaPemeranLulu TobingOctavianus Rysiat MuabuayMinus Coneston KarobaAdi KurdiPhilipus Ramendei ThamoVivaldi Gorys AronggearSylvia Roselani SamberSonya BaransanoPenata musikFahmi AlatasSinematograferShamirBarly Juan FibriadyPenyuntingArturo GPFredy AryantoPuri ChrisantyAndhy PulungPerusahaanproduksiC & T ProductionsPrima EntertainmentSET Film WorkshopDistributorC & T Production...

Kawasan Konservasi perairan Daerah Lombok Timur (KKPD Lombok Timur) adalah salah satu kawasan konservasi perairan daerah yang ada di Nusa Tenggara Barat, Indonesia. Dalam pembagian administratif Indonesia, KKPD Lombok Timur berada di wilayah administratif Kabupaten Lombok Timur. Nama lainnya adalah Kawasan Konservasi Laut Daerah Gili Sulat dan Gili Lawang. Dasar hukum penetapannya adalah Surat Keputusan Bupati Lombok Timur Nomor 188.45/332/KP/2014. Surat keputusan ini diterbitkan pada tanggal...

Voce principale: Associazione Calcio Siena. SS RoburStagione 1923-1924Sport calcio Squadra Robur Allenatore Pietro Piselli Seconda Divisione8º posto nel girone F (retrocesso in Terza Divisione) 1922-1923 1924-1925 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti la squadra di calcio italiana Società Sportiva Robur nelle competizioni ufficiali della stagione 1923-1924. Indice 1 Divise 2 Rosa 3 Statistiche 3.1 Statistiche di squadra 3.2 Statistich...

Kabupaten Boven DigoelKabupatenMonumen patung Mohammad Hatta LambangMotto: Nup Bagen Ngup BagenepPetaKabupaten Boven DigoelPetaTampilkan peta Maluku dan PapuaKabupaten Boven DigoelKabupaten Boven Digoel (Indonesia)Tampilkan peta IndonesiaKoordinat: 6°S 140°E / 6°S 140°E / -6; 140Negara IndonesiaProvinsiPapua SelatanTanggal berdiri25 Oktober 2002Dasar hukumUU Nomor 26 Tahun 2002[1]Ibu kotaTanah MerahJumlah satuan pemerintahan Daftar Distrik: 20Kamp...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

「俄亥俄」重定向至此。关于其他用法,请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號:七葉果之州地图中高亮部分为俄亥俄州坐标:38°27'N-41°58'N, 80°32'W-84°49'W国家 美國加入聯邦1803年3月1日,在1953年8月7日追溯頒定(第17个加入联邦)首府哥倫布(及最大城市)政府 • 州长(英语:List of Governors of {{{Name}}}]]) •&...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يوليو 2019) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسي...

豪栄道 豪太郎 場所入りする豪栄道基礎情報四股名 澤井 豪太郎→豪栄道 豪太郎本名 澤井 豪太郎愛称 ゴウタロウ、豪ちゃん、GAD[1][2]生年月日 (1986-04-06) 1986年4月6日(38歳)出身 大阪府寝屋川市身長 183cm体重 160kgBMI 47.26所属部屋 境川部屋得意技 右四つ・出し投げ・切り返し・外掛け・首投げ・右下手投げ成績現在の番付 引退最高位 東大関生涯戦歴 696勝493敗...

تعليم دينيمعلومات عامةصنف فرعي من تعليم المُؤَلِّف Richard Dehmel (en) يدرسه religion didactics (en) يمارسها religious education teacher (en) رمز تصنيف البرامج التعليمية 39.0439.0401 تعديل - تعديل مصدري - تعديل ويكي بيانات السجناء المدانين يتلقون التعليم القرآني في فيصل آباد بالسجن المركزي،باكستان في عام 2010 يس�...

Wappen Deutschlandkarte Basisdaten Koordinaten: 47° 39′ N, 7° 44′ O47.6452777777787.7402777777778333Koordinaten: 47° 39′ N, 7° 44′ O Bundesland: Baden-Württemberg Regierungsbezirk: Freiburg Landkreis: Lörrach Höhe: 333 m ü. NHN Fläche: 46,85 km2 Einwohner: 10.339 (31. Dez. 2022)[1] Bevölkerungsdichte: 221 Einwohner je km2 Postleitzahl: 79585 Vorwahl: 07627 Kfz-Kennzeichen: LÖ Gemeindeschlüss...

International cultural movement active from the 1920s to the 1950s SurrealismThe Treachery of Images, by René Magritte (1929), featuring the declaration Ceci n'est pas une pipe (This is not a pipe)Years active1920s–1950sLocationFrance, BelgiumMajor figuresBreton, Carrington, Dalí, Ernst, Fini, Magritte, OppenheimInfluencesSymbolismAbstract artMetaphysical paintingDadaInfluencedAbstract expressionismFantastic artPostmodern art Part of a series onSurrealism Surrealist Manifesto Surrealist c...

تحتاج هذه المقالة إلى تنسيق لتتناسب مع دليل الأسلوب في ويكيبيديا. فضلًا، ساهم بتنسيقها وفق دليل الأسلوب المعتمد في ويكيبيديا. (أبريل 2019) المعتزلة الدين الإسلام المؤسس عمرو بن عبيد وواصل بن عطاء تاريخ الظهور منتصف القرن الثاني الهجري مَنشأ البصرة بالعراق الأصل أهل السنة وا�...

This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources. Lists of battles Before 301 301–1300 1301–1600 1601–1800 1801–1900 1901–2000 2001–current Naval Sieges See also Part of a series onWarOutline History Prehistoric Ancient Post-classical castles Early modern pike and shot napoleonic Late modern industrial fourth-gen Military Organization Command and control Defense ministry Army ...

Terrorism motivated by left-wing or far-left ideologies Damage resulted from the bombing outside of the Chamber of the United States Senate on November 7, 1983. The bombing was a retaliation hit against U.S. military involvement in Lebanon and Grenada.[1] Part of a series onTerrorism Definitions History Incidents By ideology Anarchist Communist Left-wing/Far-left Narcotics-driven Nationalist Right-wing/Far-right Religious Buddhist Christian (Mormon) Hindu Islamic (Salafi-Wahhabi) Jewi...

Monorail line in Xi'an, China Xi'an Qujiang Sightseeing MonorailOverviewLocaleQujiang New District, Xi'anTransit typestraddle-beam monorailNumber of lines1Number of stations9OperationBegan operation1 May 2023; 13 months ago (2023-05-01)Number of vehicles3TechnicalSystem length6.8 km (4.23 mi)Track gauge500 mmTop speed40 km/h Map of Qujiang Sightseeing Monorail A section of the guideway The Xi'an Qujiang Sightseeing Monorail (Chinese: 西安曲江观光轻轨; p...

View of Segreganset River at low tide, Dighton, Massachusetts The Segreganset River is a small river in Bristol County, Massachusetts that flows 9.6 miles (15.4 km)[1] in a southeasterly direction through Taunton and Dighton into the Taunton River.[2] Named tributaries include the Maple Swamp, Poppasquash Swamp, Sunken Brook and Cedar Swamp. The USGS maintains a gaging station on the Segreganset River near Center Street in Dighton.[3] See also Cole River Taunton R...

2000 greatest hits album by Special EdThe Best of Special EdGreatest hits album by Special EdReleasedApril 14, 2000GenreHip hopProducerHowie TeeSpecial Ed chronology Revelations(1995) The Best of Special Ed(2000) Still Got It Made(2004) Professional ratingsReview scoresSourceRatingAllMusic[1] The Best of Special Ed is the greatest hits album by the rapper Special Ed, released in 2000. Track listing I Got It Made Neva Go Back Come On, Let's Move It I'm the Magnificent (The Magn...

Defunct American motor vehicle manufacturer 1929 Durant Deluxe Roadster 4-40 at Stahls Automotive Collection The Durant was a make of automobile assembled by Durant Motors Corporation of New York City, New York from 1921 to 1926 and again from 1928 to 1932. Durant Motors was founded by William Billy Durant after he was terminated, for the second and final time, as the head of General Motors. Billy Durant's intent was to build an automotive empire that could one day challenge General Motors. T...












