Nombre de Bodenstein
|
Read other articles:

ComtéNegara asalPrancisWilayahJuraSumber susuSapiDipasteurisasiTidakTeksturKerasKadar lemak45%Waktu pematangan3 bulanSertifikasiAOC: 1958[1] Comté adalah keju dari daerah Jura di Prancis yang menggunakan susu sapi mentah.[1] Keju Comté ini merupakan keluarga dari keju Gruyère yang dibuat di Prancis.[2] Susu yang digunakan dalam pembuatan keju Comté hanyalah susu yang berasal dari sapi jenis Montbéliard dan Pie-Rouge.[1] Susu tersebut merupakan susu yang d...

Cuka balsamik Cuka balsamik (bahasa Italia: aceto balsamico) adalah cuka yang sangat gelap, pekat, dan beraroma kuat yang berasal dari Italia, dibuat seluruhnya atau sebagian dari anggur. Anggur harus adalah jus anggur yang baru saja dihancurkan dengan semua kulit, biji dan batang. Istilah aceto balsamico tidak diatur, tetapi ada tiga cuka balsamic yang dilindungi: Aceto Balsamico Tradizionale di Modena DOP (Cuka Balsamik Tradisional Modena), Aceto Balsamico Tradizionale di Reggio Emilia ...

Joseph Smith Presiden Gerakan Orang Suci Zaman Akhir ke-106 April 1830 (1830-04-06) – 27 Juni 1844 (1844-06-27)Digantikan olehBrigham YoungWali Kota Nauvoo, IllinoisMasa jabatan19 Mei 1842 (1842-05-19) – 27 Juni 1844 (1844-06-27)Didahului olehJohn C. BennettDigantikan olehChancy Robison[1] Informasi pribadiLahirJoseph Smith, Jr.(1805-12-23)23 Desember 1805Sharon, Vermont, Amerika SerikatMeninggal27 Juni 1844(1844-06-27) (umur 38)Cathage...
Monasteri Dionysiou, kodeks 90, sebuah manuskrip abad ke-13 yang berisi karya-karya pilihan dari Herodotus, Plutarch dan (yang ditampilkan di sini) Diogenes Laertius Kehidupan dan Pendapat Filsuf-filsuf Tersohor (Yunani: Βίοι καὶ γνῶμαι τῶν ἐν φιλοσοφίᾳ εὐδοκιμησάντων; Latin: Vitae Philosophorumcode: la is deprecated ) adalah sebuah biografi para filsuf Yunani karya Diogenes Laërtius. Karya tersebut ditulis dalam bahasa Yunani, diyakini pada par...

Apparalang Lokasi di Indonesia Informasi Lokasi Desa Ara, Kecamatan Bontobahari Kabupaten Bulukumba, Sulawesi Selatan Negara Indonesia Koordinat 5°31′16″S 120°25′48″E / 5.521°S 120.43°E / -5.521; 120.43Koordinat: 5°31′16″S 120°25′48″E / 5.521°S 120.43°E / -5.521; 120.43 Awal pembangunan Kalo gak salah 2016 Jenis objek wisata objek wisata Bahari Apparalang adalah objek wisata bahari yang berlokasi di Desa Ara, Kecam...

Antwerp (Belanda: Antwerpencode: nl is deprecated ) Negara Belgia Region Region Flandria Ibu kota Antwerp Area 2,867 km² Populasi 1/1/2008 1,715,707 Kepadatan 587 / km² Gubernur Cathy Berx Official Site Provinsi Antwerpen (Belanda Provincie Antwerpen, Prancis Province d'Anvers) adalah sebuah provinsi di negara bagian Flandria, Belgia. Provinsi ini memiliki ibu kota Antwerpen. Pembagian administratif Provinsi ini dibagi menjadi tiga arondisemen administratif (Belanda: arrondissementencode: ...

Edward BalliolEngravir abad ke-18 Edward BalliolPengklaim Tahta SkotlandiaBerkuasaSeptember 1332 sampai 1336Informasi pribadiKelahiranc. 1283Kematians. 1367Wheatley, DoncasterWangsaWangsa BalliolAyahJohn BalliolIbuIsabella de WarenneAgamaKatolik Roma Edward Balliol (c. 1283 – 1367) adalah seorang pengklaim tahta Skotlandia (1314–1356). Dengan bantuan Inggris, ia memerintah sebagian negara tersebut selama tiga periode antara 1332 dan 1336. Kehidupan Segel Edward Balliol, Raja Skotlan...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Aiko 16-Sai (アイコ十六歳code: ja is deprecated ) adalah sebuah novel Jepang karya Akemi Hotta. Novel ini telah diadaptasikan ke serial televisi pada tahun 1982 dan film pada tahun 1983. Film アイコ十六歳Aiko 16-SaiSutradaraAkiyoshi Imazek...

2010 Pakistani military operation This article may require copy editing for grammar, style, cohesion, tone, or spelling. You can assist by editing it. (August 2023) (Learn how and when to remove this template message) Operation Khwakh Ba De ShamPart of the Insurgency in Khyber PakhtunkhwaThe Orakzai Agency highlighted in yellowDateBattle phase: In Kurram, September 2009[1] - June 2010. Battle phase: In Orakzai, March 2010 - June 2010 Insurgency phase: June 2010 - January 2011LocationK...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bodrogolaszi – news · newspapers · books · scholar · JSTOR (September 2020) (Learn how and when to remove this template message) Village in Northern Hungary, HungaryBodrogolasziVillage FlagCoat of armsBodrogolasziLocation of BodrogolasziCoordinates: 48°17′08...

Liga Negara UEFA 2024–2025Informasi turnamenJadwalpenyelenggaraanFase Liga:5 September – 19 November 2024Perempat final Liga A danperebutan tempat promosi/degradasi Liga A/B dan B/C:20–23 Maret 2025Babak final:4–8 Juni 2025Perebutan tempat promosi/degradasi Liga C/D:26–31 Maret 2026Jumlahtim peserta54← 2022–2023 2026–2027 → Liga Negara UEFA 2024–2025 adalah musim keempat Liga Negara UEFA, sebuah kompetisi sepak bola internasional yang melibatkan tim-tim nasional pr...

Currency of Georgia Georgian lariქართული ლარი (Georgian) ISO 4217CodeGEL (numeric: 981)Subunit0.01UnitUnitlariPluralThe language(s) of this currency do(es) not have a morphological plural distinction.Symbol₾, ლ, (GEL[1])DenominationsSubunit 1⁄100tetriBanknotes Freq. used₾5, ₾10, ₾20, ₾50, ₾100 Rarely used₾1, ₾2, ₾200Coins5, 10, 20, 50 tetri, ₾1, ₾2DemographicsDate of introduction1995ReplacedGe...

Un groupe de personnes d'affaires dans les années 1980. Une personnalité du monde des affaires[1], un homme d'affaires[2] ou une femme d'affaires, par opposition à un cadre, est une personne qui a créé une ou plusieurs sociétés commerciales, ou qui les administre, profitant des revenus qu'elles produisent. Le terme d'« entrepreneur » désigne quant à lui une personne qui crée une entreprise ou qui entreprend une activité professionnelle. Les termes de « femme d'aff...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

School of Tibetan Buddhism Statue of the 16th Karmapa at Samye Ling, Scotland, wearing the famed black crown of the Karmapas, the traditional heads of the Karma Kagyu lineage Part of a series onTibetan Buddhism Schools Nyingma Kadam Sakya Bodong Kagyu Jonang Gelug Rimé Key personalities First dissemination Padmasambhāva Śāntarakṣita Kamalaśīla Songtsen Gampo Trisong Detsen Ralpacan Second dissemination Atiśa Talika Abhayakirti Niguma Sukhasiddhi Milarepa Nyingma Yeshe Tsogyal Longche...

Untuk aktris Agle Janam Mohe Bitiya Hi Kijo, lihat Fatima Sana Shaikh. Sana Amin SheikhSheikh di Penghargaan Golden Petal di 2016Lahir10 Agustus 1989 (umur 34)Mumbai, Maharashtra, IndiaKebangsaanIndianPekerjaanAktris Radio JockeyTahun aktif1995-sekarangSuami/istriAijaz Sheikh (m. 2016) Sana Amin Sheikh adalah seorang aktris dan joki radio India.[1][2] Ia terkenal karena peran utamanya sebagai Ritu Shah di Disney Channel India Original S...

Abderrazak HamdallahHamdallah nel 2023Nazionalità Marocco Altezza185 cm Peso84 kg Calcio RuoloAttaccante Squadra Al-Ittihād CarrieraGiovanili 2006-2010 Olympique Safi Squadre di club1 2009-2013 Olympique Safi55 (30)2013 Aalesund27 (15)2014-2015 Guangzhou R&F32 (25)2015-2017 Al-Jaish48 (21)2017-2018 Al-Rayyan20 (18)2018-2022 Al-Nassr80 (81)2022- Al-Ittihād50 (39) Nazionale 2012- Marocco24 (6) 1 I due numeri indicano le presenze e le reti...

For other people with the same name, see Anthony Wilson. British record producer, record owner and television presenter (1950–2007) Tony WilsonHosting TV discussion After Dark in 2003BornAnthony Howard Wilson(1950-02-20)20 February 1950Pendleton, Salford, Lancashire, EnglandDied10 August 2007(2007-08-10) (aged 57)Withington, Manchester, EnglandResting placeSouthern Cemetery, Chorlton-cum-Hardy, ManchesterEducationBA in EnglishAlma materJesus College, CambridgeOccupationsJournalist...

American baseball player (1933-2013) Baseball player Ed BoucheeFirst basemanBorn: (1933-03-07)March 7, 1933Livingston, Montana, U.S.Died: January 23, 2013(2013-01-23) (aged 79)Phoenix, Arizona, U.S.Batted: LeftThrew: LeftMLB debutSeptember 19, 1956, for the Philadelphia PhilliesLast MLB appearanceJuly 24, 1962, for the New York MetsMLB statisticsBatting average.265Home runs61Runs batted in290 Teams Philadelphia Phillies (1956–1960) Chicago Cubs (1960–196...
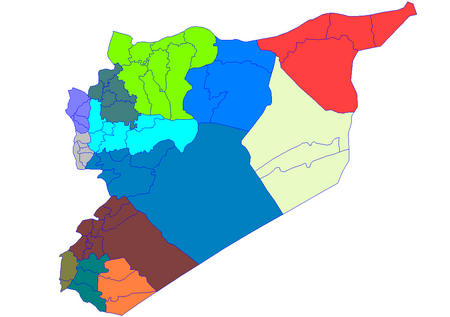
Cet article est une ébauche concernant une localité syrienne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. HarimHarenc Localisation Pays Syrie Gouvernorat Idleb Coordonnées 36° 12′ 27″ nord, 36° 31′ 09″ est Altitude 160 m Géolocalisation sur la carte : Syrie HarimHarim Géolocalisation sur la carte : Turquie HarimHarim modifier Harim, Harrim (en...



