Mécanique newtonienne
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2020. Daftar wali kota Las Vegas, Nevada ini dikumpulkan dari dokumen domain umum yang disediakan oleh Pegawai Kota. Wali kota Las Vegas Masa Wali kota Catatan 1911-1913 Peter Buol 1913-1919 W. L. Hawkins 1919-1921 W. E. Ferron 1921 Horace Jones Meninggal keti...

Agama di Etiopia (2015)[1] Ortodoks Etiopia (39.1%) Islam (31.3%) Protestan (28.2%) Lainnya dan tidak ada (2.5%) Katedral Tritunggal Kudus di Addis Ababa. Etiopia adalah salah satu wilayah pertama di dunia yang menganut Kristen. Agama di Etiopia terdiri dari sejumlah keyakinan. Keyakinan-keyakinan tersebut utamanya meliputi agama-agama Abrahamik, jumalh terbesar adalah Kekristenan (Ortodoks Etiopia, Pentay, Katolik Roma) yang meliputi 67.3...

Basílica de Santa María la Real de Covadonga/CuadongaBasilika Santa Maria dari Kebangsawanan CovadongaBasilika Santa Maria dari Kebangsawanan CovadongaLokasiCovadonga/Cuadonga, Cangas de Onís/Cangues d'Onís, AsturiasNegara SpanyolDenominasiGereja Katolik RomaSejarahDedikasiBunda dari CovadongaTanggal konsekrasi11 September 1901KultusCatholicArsitekturStatusBasilika minorStatus fungsionalAktifArsitekRoberto FrassinelliGayaNeo-RomanesquePeletakan batu pertama1877Selesai1901Administrasi...

Merton Miller Merton Howard Miller (Boston, Massachusetts, 16 Mei 1923 – 3 Juni 2000) adalah ekonom Amerika Serikat yang pernah bekerja sebagai ekonom dalam divisi penelitian pajak di Departemen Perbendaharaan selama PD II, dan menerima Ph.D. dalam ilmu ekonomi dari Johns Hopkins University, 1952. Pada 1958, ia berkolaborasi dengan Franco Modigliani untuk menulis The Cost of Capital, Corporate Finance and the Theory of Investment. Karya ini mendorong penolakan fundamental pada pandangan tra...

Untuk kapal, silakan baca Wilhelm Gustloff (kapal) Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Wilhelm Gustloff – berita · surat kabar · buku · cendekiawan · JSTORWilhelm Gustloff BiografiKelahiran30 Januari 1895 Schwerin Kematian4 Februari 1936 (...

American airline from 1967 to 1982 Altair Airlines IATA ICAO Callsign AK ALT ALTAIR Founded1967Ceased operations1982Fleet size9 (in 1982)HeadquartersPhiladelphia, Pennsylvania, United StatesKey peopleHenry P. Hill Altair Airlines was an airline based in Philadelphia. It was in service from 1967 to 1982. According to its June 15, 1982 system timetable, the Altair name was taken from the first magnitude star Altairius brightest in the constellation Aquila (Eagle) from which the airline's Blue E...

Fulford PlaceLocation287 King Street EastBrockville, OntarioBuilt1899–1901Built forGeorge Taylor FulfordOriginal usePrivate residenceCurrent useHistoric house museumArchitectAlbert W. Fuller (house)Olmsted Brothers (garden)Governing bodyOntario Heritage TrustWebsiteFulford Place webpage National Historic Site of CanadaDesignated1992 Fulford Place is a historic mansion in Brockville, Ontario. It was completed in 1901 for Senator George Taylor Fulford, a Canadian businessman and politician. ...

American politician Linn Boyd20th Speaker of the United States House of RepresentativesIn officeDecember 1, 1851 – March 3, 1855Preceded byHowell CobbSucceeded byNathaniel P. BanksLeader of the House Democratic CaucusIn officeDecember 1, 1851 – March 3, 1855Preceded byHowell CobbSucceeded byJames Lawrence OrrMember of the U.S. House of Representativesfrom Kentucky's 1st districtIn officeMarch 4, 1839 – March 3, 1855Preceded byJohn L. MurraySucc...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (décembre 2020). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ...

Nick Stahl nel 2023 Nicolas Kent Stahl (Harlingen, 5 dicembre 1979) è un attore statunitense. Indice 1 Biografia 2 Vita privata 3 Filmografia 3.1 Cinema 3.2 Televisione 4 Doppiatori italiani 5 Riconoscimenti 6 Altri progetti 7 Collegamenti esterni Biografia Nato in Texas, inizia la sua carriera da bambino, partecipando ad alcuni spot pubblicitari e due film TV. La grande occasione arriva nel 1993 quando viene scelto da Mel Gibson per L'uomo senza volto; in seguito recita nel film Ritrovarsi ...
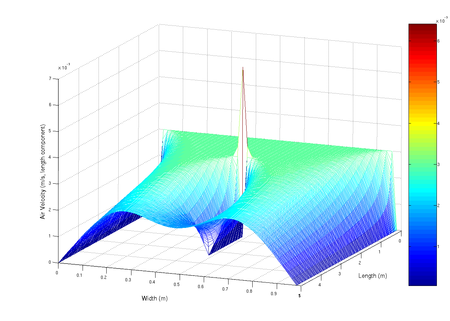
Persamaan diferensial adalah persamaan matematika untuk fungsi satu variabel atau lebih, yang menghubungkan nilai fungsi itu sendiri dan turunannya dalam berbagai orde. Persamaan diferensial memegang peranan penting dalam rekayasa, fisika, ilmu ekonomi dan berbagai macam disiplin ilmu lain. Visualisasi aliran udara ke dalam saluran dimodelkan sesuai persamaan Navier-Stokes Persamaan diferensial muncul dalam berbagai bidang sains dan teknologi, bilamana hubungan deterministik yang melibatkan b...

Italian maker of musical instruments Cristofori redirects here. For the surname, see Cristofori (surname). For other uses, see Cristofori (disambiguation). Bartolomeo CristoforiPhoto of a 1726 portrait of Bartolomeo Cristofori. The original was lost in the Second World War.BornBartolomeo Cristofori di Francesco(1655-05-04)May 4, 1655Padua, Republic of VeniceDiedJanuary 27, 1731(1731-01-27) (aged 75)Florence, Grand Duchy of TuscanyOccupation(s)Inventor, instrument makerKnown forInven...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2016) أوزبكستان في الألعاب الأولمبية علم أوزبكستان رمز ل.أ.د. UZB ل.أ.و. اللجنة الأولمبية الوطنية لجمه...

PakenhamInformasi umumJenis layananLayanan suburban MelbourneStatusOperasionalDaerah operasiMelbourne, Victoria, AustraliaOperator saat iniMetro TrainsLintas pelayananStasiun awalFlinders StreetJumlah pemberhentian27 (tidak termasuk stasiun City Loop)Stasiun akhirPakenhamJarak tempuh569 km (354 mi)Waktu tempuh rerata1 jam 9 menitFrekuensi perjalanan7–14 minutes weekdays peak20 minutes weekdays off-peak and weekend daytime30 minutes weekend nights60 minutes early weekend morningsDo...

يعلن بن سعد معلومات شخصية الحياة العملية المهنة شاعر بوابة الأدب تعديل مصدري - تعديل يُعلِن بن سعد بن غمر من بني سعد بن خولان. من شعراء خولان ورُماتها، كان ساحب حصن (التلمّص) بناحية صعدة في اليمن، معاصراً لسيف ابن ذي يزن، وسُمّي (مغرقاً) على جده عمرو بن زيد، وميزوا هذا ...

Unincorporated community in Florida, United States Florahome, Florida unincorporated communityFlorahome's former railroad station on Coral Farms Road, now an antique shop.Country United StatesState FloridaCounty PutnamZIP code32140 Pulverized peat in bags loaded on tram cars, Florahome, 1944 Florahome is an unincorporated community in Putnam County, Florida, United States, located on State Road 100. The town was established in 1899 by the Georgia Southern and Florida Railway. ...

Class hi residues Protein tyrosine kinasepdb 2HCK, rendered in PyMOLIdentifiersSymbolPkinase_TyrPfamPF07714InterProIPR001245SMARTTyrKcPROSITEPDOC00629SCOP21apm / SCOPe / SUPFAMOPM superfamily186OPM protein2k1kCDDcd00192Membranome3Available protein structures:Pfam structures / ECOD PDBRCSB PDB; PDBe; PDBjPDBsumstructure summary A tyrosine kinase is an enzyme that can transfer a phosphate group from ATP to the tyrosine residues of specific proteins inside a cell. It functions as an ...

4 Hours of SilverstoneFIA World Endurance ChampionshipVenueSilverstone CircuitCorporate sponsorAutosportFirst race1976First FIA WEC race2012Duration4 HoursPrevious names1000 Kilometres of Silverstone6 Hours of SilverstoneMost wins (driver) Jacky Ickx (4) Jochen Mass (4) Allan McNish (4)Most wins (team) Silk Cut Jaguar (5)Most wins (manufacturer)Porsche (7) The 4 Hours of Silverstone (formerly the 1000 km of Silverstone and 6 Hours of Silverstone) is an endurance sports car race held at S...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Culture of Europe – news · newspapers · books · scholar · JSTOR (July 2017) (Learn how and when to remove t...

American journalist, editor, and publisher (1893–1976) Freda KirchweyBornMary Frederika Kirchwey(1893-09-26)September 26, 1893Lake Placid, New YorkDiedJanuary 3, 1976(1976-01-03) (aged 82)Alma materBarnard CollegeOccupationJournalistSpouseEvans Clark Mary Frederika Freda Kirchwey (September 26, 1893 – January 3, 1976) was an American journalist, editor, and publisher strongly committed throughout her career to liberal causes (anti-Fascist, pro-Soviet, anti-anti-communist). F...

