Longueur
|
Read other articles:

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Monsters UniversityBerkas:Monsters University.jpgPoster bioskopSutradaraDan ScanlonProduserKori RaeSkenarioDaniel GersonRobert L. BairdDan Scanlon[1]CeritaDaniel GersonRobert L. BairdDan ScanlonPemeranBilly CrystalJohn GoodmanSteve BuscemiPenata musikRandy NewmanSinematograferMatt AspburyJean-Claude KalachePenyuntingGreg SnyderPerusahaanproduksiWalt Disney PicturesPixar Animation StudiosDistributorWalt Disney Studios Motion PicturesTanggal rilis 5 Juni 2013 (2013-06-05) ...
1939 novel by James Joyce This article is about the book. For the street ballad after which it is named, see Finnegan's Wake. For the Tangerine Dream album, see Finnegans Wake (album). Finnegans Wake AuthorJames JoyceLanguageEnglishPublisherFaber and FaberPublication date4 May 1939OCLC42692059Dewey Decimal823/.912 21LC ClassPR6019.O9 F5 1999Preceded byUlysses (1922) Finnegans Wake is a novel by Irish writer James Joyce. It is known for its experimental style and its reputation...

Sporting event delegationEcuador at the2017 World Aquatics ChampionshipsFlag of EcuadorFINA codeECUNational federationFederación Ecuatoriana de NataciónWebsitewww.fena-ecuador.orgin Budapest, HungaryCompetitors8 in 2 sportsMedalsRanked 22nd Gold 0 Silver 1 Bronze 0 Total 1 World Aquatics Championships appearances197319751978198219861991199419982001200320052007200920112013201520172019202220232024 Ecuador is scheduled to compete at the 2017 World Aquatics Championships in Budapest, Hungary f...

American comedy-drama television series (1977–1981) Not to be confused with Eight Is Enough (comics). Eight Is EnoughGenreComedy drama, SitcomBased onEight Is Enoughby Tom BradenDeveloped byWilliam BlinnStarringDick Van PattenDiana HylandBetty BuckleyGrant GoodeveLani O'GradyLaurie WaltersSusan RichardsonDianne KayConnie NewtonWillie AamesAdam RichTheme music composerFred Werner (Season 1 & 2 opening theme)Song: from Season 3 onwards – Eight Is Enough Music by Lee HoldridgeLyrics by M...

Ancient Greek statue Lion of KnidosLion of KnidosMaterialMarbleSize2.89 m long by 1.82 m highCreatedc. 350–200 BCPresent locationBritish Museum, LondonRegistration1859,1226.24 The Lion of Knidos is the name for a colossal ancient Greek statue erected near the ancient port of Knidos, south-west Asia Minor (now near Datça in Turkey). Although there is some debate about the age of the sculpture, in general, scholarly opinion dates it to the 2nd century BC. Since 2000, it has been promin...

Beauty pageant Miss Indonesia 2013DateFebruary 20, 2013PresentersDaniel Mananta, Jennifer Sumia, Ovi Dian Aryani, Javier JustinEntertainmentNOAH, Bunga Citra Lestari, Cakra Khan, Febri Idol, Yoda Idol, Dion IdolVenueHall D2 Jakarta International Expo , JakartaBroadcasterRCTIEntrants33Placements10WinnerVania Larissa West Kalimantan← 20122014 → Miss Indonesia 2013 was the ninth edition of the Miss Indonesia beauty pageant, held on February 20, 2013 at Jakarta Internationa...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

County Seat of Skagit County, Washington, United States This article is about the city in Washington State. For the former plantation of George Washington, see Mount Vernon. City in Washington, United StatesMount VernonCityFirst Street FlagNickname: City of TulipsLocation of Mount Vernon in Washington StateMount VernonLocation of Mount Vernon in the United StatesCoordinates: 48°25′12″N 122°19′34″W / 48.42000°N 122.32611°W / 48.42000; -122.32611CountryU...

Former British protected states in the Malay Peninsula This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Unfederated Malay States – news · newspapers · books · scholar · JSTOR (August 2023) (Learn how and when to remove this message) Not to be confused with Federated Malay States. Unfederated Malay StatesNeger...

Layer inside a planet between core and crust For other uses, see Mantle (disambiguation). A mantle is a layer inside a planetary body bounded below by a core and above by a crust. Mantles are made of rock or ices, and are generally the largest and most massive layer of the planetary body. Mantles are characteristic of planetary bodies that have undergone differentiation by density. All terrestrial planets (including Earth), a number of asteroids, and some planetary moons have mantles. Example...

IxkunLapangan utara dengan Prasasti 1 dan 2Lokasi di Guatemala modernLokasiDoloresWilayahDepartemen Petén, GuatemalaKoordinat16°34′25″N 89°24′40″W / 16.57361°N 89.41111°W / 16.57361; -89.41111SejarahPeriodeKlasik AkhirBudayaPeradaban MayaCatatan situsArkeologJuan Pedro Laporte Atlas Arqueológico de Guatemala Ixkun (Ixcún atau Ixkún dalam ortografi Spanyol) adalah sebuah situs arkeologi Maya pra-Kolumbus, yang terletak di wilayah Cekungan Petén, s...

Go by A map of Belize Main article: Geography of Belize The country of Belize has roughly 386 km of coastline, and has many coral reefs, cayes, and islands in the Caribbean Sea. Most of these form the Belize Barrier Reef, the longest in the western hemisphere stemming approximately 322 km (200 mi). The reef and its islands have been a UNESCO World Heritage Site since 1996. Caribbean cayes The following is a list of oceanic islands of Belize, arranged according to region but all...

Pour les articles homonymes, voir In vitro (homonymie). Culture in vitro d'un plant de vigne, de la Forschungsanstalt Geisenheim. In vitro (en latin : « sous verre ») s'applique à toute activité expérimentale réalisée sur micro-organismes, organes ou cellules en dehors de leur contexte naturel (en dehors de l'environnement, de l'organisme vivant ou de la cellule) et en conditions définies et contrôlées. Un exemple est la fécondation in vitro (FIV). Étymologie et ca...
Mihajlo Idvorski PupinPupin sekitar tahun 1890Lahir(1858-10-09)9 Oktober 1858Idvor, Kekaisaran Austria(sekarang Serbia)Meninggal12 Maret 1935(1935-03-12) (umur 76)Kota New York, A.S.Warga negaraAustria (1858–1883)Amerika (1883–1935)AlmamaterColumbia CollegeDikenal atasKomunikasi telepon jarak jauhPenghargaanElliott Cresson Medal (1905)IEEE Medal of Honor (1924)[1]Edison Medal[2] (1920)Pulitzer Prize (1924)John Fritz Medal (1932)Karier ilmiahBidangFisika, PenemuanMaha...

Star WorldLogo Star World yang digunakan di Hong Kong, Taiwan, Timur Tengah, Afrika Utara dan Asia TenggaraDiluncurkan15 Desember 1994Ditutup1 Oktober 2017 (Asia Tenggara, Hong Kong dan Vietnam) (kecuali Timur Tengah, India, Tiongkok, Taiwan, Pakistan, Asia Selatan)15 Maret 2023 (India)1 Januari 2024 (Taiwan)PemilikFox Networks GroupNegaraHong KongBahasaInggrisKantonHindiMandarinArabKantor pusatHong KongMumbaiSaluran seinduk Daftar Star MoviesFox Movies (MENA)FoxFox (Arabia)National Geographi...
Road in New South Wales, Australia This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Appin Road – news · newspapers · books · scholar · JSTOR (August 2022) (Learn how and when to remove this message) Appin RoadNew South WalesHeading south along Appin Road, CampbelltownNorth endSouth endCoordinates 34°04′30�...
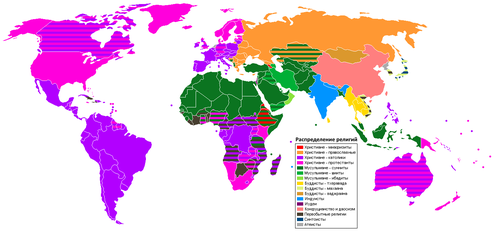
Конфе́ссия (от лат. confessio — «испове́дание»), также вероиспове́дание — особенность вероисповедания в пределах определённого религиозного учения[1][2][3][4][5][6], а также объединение верующих, придерживающихся этого вероисповедания. Например,...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) ← 2015 2014 2013 2016 في روسيا → 2017 2018 2019 عقود: طالع أيضاً:أحداث أخرى 2016تاريخ روسيا • جدول زمني • قائِمة فيما يلي �...

Pour les articles homonymes, voir Louis Salleron. le Salleron Le Salleron à Ingrandes, en 2011. Cours du Salleron. Caractéristiques Longueur 51,74 km [1] Bassin 157 km2 Bassin collecteur Loire Débit moyen 1,0 m3/s (Journet) Nombre de Strahler 4 Organisme gestionnaire SMABCAC Régime Pluvial Cours Source le Douet · Localisation Azat-le-Ris · Altitude 247 m · Coordonnées 46° 16′ 45″ N, 1° 04′ 16″ E Confluence l'Anglin · Locali...









![{\displaystyle \scriptstyle \left[x(\tau ),y(\tau ),z(\tau )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f99326174cf12a554c0a9ee80731dfa201dcb72)
![{\displaystyle L(t)=\int _{o}^{t}\left\Vert {\overrightarrow {\partial P \over \partial \tau }}\right\Vert \mathrm {d} \tau =\int _{o}^{t}{\sqrt {\left[{\partial x \over \partial \tau }\right]^{2}+\left[{\partial y \over \partial \tau }\right]^{2}+\left[{\partial z \over \partial \tau }\right]^{2}}}\,\mathrm {d} \tau }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b263e24a757602961166184ffd4d94d255fe3fef)







