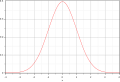
Interconnexions entre la théorie des probabilités et la statistique
|
Read other articles:

This article is about the M.I.A. music video. For the Kid Rock music video, see Born Free (Kid Rock song) § Music video. 2010 American filmBorn FreeDirected byRomain GavrasWritten byRomain Gavras[1] Maya ArulpragasamStarringIan HamrickCinematographyAndre ChemetoffMusic byMaya M.I.A. ArulpragasamDistributed byXL Recordings Interscope Geffen A&MRelease date26 April 2010 (premiere)Running time9:06CountryUnited StatesLanguageEnglishBudget$250,000 (estimated) Born Free is the mus...

RedOneInformasi latar belakangNama lahirNadir KhayatLahir9 April 1972 (umur 51) Tétouan, MarokoAsalMoroccoGenreHouse, pop, dance, Electronica, R&B, hip-hopPekerjaanProducer, songwriter, Music executive, singer, rapperTahun aktif2003–presentLabel2101 RecordsArtis terkaitLady Gaga, Jennifer Lopez, Paulina Rubio, Mohombi, Porcelain BlackSitus webredoneprod.com Nadir Khayat (lahir 9 April 1972), lebih dikenal dengan nama panggung RedOne, lahir di Tétouan, Maroko[1] dan merupa...

Parlement van GriekenlandΒουλή των Ελλήνων (Grieks) Wetgevend orgaan van Griekenland Algemene informatie Opgericht in 1843 Aantal leden 300 Ontmoetingsplaats Oude Koninklijke Paleis, Athene Huidige legislatuur Voorzitter Zoi Konstantopoulou Portaal Politiek Het Griekse parlementsgebouw in Athene. Het Parlement van Griekenland (Grieks: Βουλή των Ελλήνων, Vouli ton Ellinon), ook bekend onder de naam Vouli, is gehuisvest in het Oude Koninklijke Pa...

العلاقات الفانواتية الهندوراسية فانواتو هندوراس فانواتو هندوراس تعديل مصدري - تعديل العلاقات الفانواتية الهندوراسية هي العلاقات الثنائية التي تجمع بين فانواتو وهندوراس.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: و

Tragny Tragny (Frankreich) Staat Frankreich Region Grand Est Département (Nr.) Moselle (57) Arrondissement Metz Kanton Faulquemont Gemeindeverband Sud Messin Koordinaten 48° 58′ N, 6° 23′ O48.9594444444446.3783333333333Koordinaten: 48° 58′ N, 6° 23′ O Höhe 230–284 m Fläche 5,43 km² Einwohner 90 (1. Januar 2020) Bevölkerungsdichte 17 Einw./km² Postleitzahl 57580 INSEE-Code 57676 Vorlage:Infobox Gemeinde in Frankreich/Wa...

James Grant of Freuchie (1616–1663) was a Scottish landowner, the seventh Laird of Freuchie. Freuchie Castle, also known as Ballachastell is now called Castle Grant. James Grant inerited Freuchie, or Ballachastell, now called Castle Grant Career He was a son of John Grant of Freuchie and Mary, daughter of Walter Ogilvie of Findlater.[1] A note written by his grandmother, Lilias Murray, indicates he was born on 24 June 1616. He became Laird of Freuchie on the death of his father in 1...

Mesjid Nasional Abuja, juga dikenal sebagai Mesjid Nasional Nigeria, di Abuja, Nigeria. Islam menurut negara Afrika Aljazair Angola Benin Botswana Burkina Faso Burundi Kamerun Tanjung Verde Republik Afrika Tengah Chad Komoro Republik Demokratik Kongo Republik Kongo Djibouti Mesir Guinea Khatulistiwa Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Pantai Gading Kenya Lesotho Liberia Libya Madagaskar Malawi Mali Mauritania Mauritius Maroko Mozambik Namibia Niger Nigeria Rwanda ...

University in Innopolis, Tatarstan, Russia Innopolis UniversityУниверситет ИннополисMain building of Innopolis UniversityEstablished10 December 2012; 10 years ago (2012-12-10) [1]Academic staff216 (2019)[2]Students800 (2019)[3]Address1 Universitetskaya Street, Innopolis, Tatarstan, 420500, Russia55°45′13.3″N 48°44′34.8″E / 55.753694°N 48.743000°E / 55.753694; 48.743000LanguageEnglishWebsiteuniver...

Chain of comic book stores based in Texas Lone Star ComicsTypeComics retailerIndustryRetailFounded1961 (as a mail order company)1977 (as a brick-and-mortar store)FounderJake Buddy SaundersDefunct2013 (continues as online retailer)HeadquartersDallas-Fort Worth metroplex, Texas, U.S.A.ProductsComics, collectiblesWebsitemycomicshop.com Lone Star Comics was a chain of comic book stores located in the Dallas-Fort Worth area in north central Texas. The chain's offerings included comic books, action...

Mexican television network Television channel Canal 6CountryMexicoUnited StatesBroadcast areaNortheast & North-Central Mexico, Greater Mexico City, Southwestern United States over-the-air,nationally throughout Mexico, Costa Rica and the United States via cable, satellite and IPTVHeadquartersMonterrey, Nuevo León, MexicoProgrammingPicture format1080i HDTVOwnershipOwnerGrupo MultimediosKey peopleFrancisco GonzálezHistoryLaunchedFebruary 24, 1968; 55 years ago (February 24, 19...

1993 in spaceflightAstronauts Story Musgrave and Jeffrey Hoffman repair the Hubble Space Telescope during STS-61.Orbital launchesFirst12 JanuaryLast22 DecemberTotal83Successes77Failures4Partial failures2National firstsSatellite PortugalRocketsMaiden flightsAriane 4 42LAtlas IIASPSLVStart-1Crewed flightsOrbital9Total travellers47vte The following is an outline of 1993 in spaceflight. vteTimeline of spaceflight Spaceflight before 1951 1950s 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959...

Gwar discographyGwar playing at Riot Fest, 2014.Studio albums15Live albums2Compilation albums2Video albums23EPs2 Gwar is an American heavy metal band formed in Richmond, Virginia in 1984. Their discography includes fifteen studio albums, two live albums, two compilation albums, and two EPs. The band has also released nine singles. Discography Studio albums Year Album details Peak chart positions Sales US[1] USIndie[2] CAN AUS 1988 Hell-O First studio album Released: September ...

American comic book writer, music critic and media personality Harvey PekarBornHarvey Lawrence Pekar(1939-10-08)October 8, 1939Cleveland, Ohio, U.S.DiedJuly 12, 2010(2010-07-12) (aged 70)Cleveland Heights, Ohio, U.S.Occupation Comic book writer filing clerk music literary critic GenreUnderground comicsAlternative comicsSubjectAutobiographyYears active1959–2010Notable worksAmerican SplendorOur Cancer YearNotable awardsInkpot Award, 1986American Book Award, 1987Harvey Award, 1995Eis...

American football team San Diego ShockwaveEstablished 2006Folded 2007Played in San Diego, Californiaat the Viejas Arena League/conference affiliationsNational Indoor Football League (2007)Current uniformTeam colorsBlack, Maroon, White MascotShock and WaveCheerleadersLady ShakersPersonnelPresidentJeff SprowlsHead coachRobert BeesTeam history San Diego Shockwave (2007) ChampionshipsLeague championships (1)2007Conference championships (0)Division championships (0)Home arena(s)...

Podcast technology company MegaphoneIndustryRadioGenrePodcastsFoundedFebruary 2015 (2015-02)[1]FoundersAndy Bowers, Brendan MonaghanHeadquartersReston, Virginia, U.S.Key peopleBrendan Monaghan (CEO)[2]Andy Bowers (CCO)[2]Matt Turck (CRO)[3]Jason Cox (CTO)[4]OwnerSpotifyNumber of employees25[5] (2016)Websitemegaphone.fm Megaphone (formerly Panoply Media)[6] is a Software as a service (SaaS) business owned by Spotify. The co...

Shanghai Metro station East Huaxia Road华夏东路View of the underground platform of the station.General informationLocationPudong, ShanghaiChinaCoordinates31°11′48″N 121°40′52″E / 31.196553°N 121.681098°E / 31.196553; 121.681098Operated byShanghai No. 2 Metro Operation Co. Ltd.Line(s) Line 2Platforms2 (2 side platforms)Tracks2ConstructionStructure typeUndergroundAccessibleYesOther informationStation codeL02/06HistoryOpenedApr...

اڤريل كوليريدج تايلور معلومات شخصيه الميلاد 8 مارس 1903[1][2][3] الوفاة 21 ديسمبر 1998 (95 سنة)[1][2][3] مواطنه المملكه المتحده المملكه المتحده لبريطانيا العظمى و ايرلاندا (–12 ابريل 1927) الاب سامويل كوليريدج تايلور الحياه العمليه المهنه ملحنه ...

この記事の主題はウィキペディアにおける人物の特筆性の基準を満たしていないおそれがあります。基準に適合することを証明するために、記事の主題についての信頼できる二次資料を求めています。なお、適合することが証明できない場合には、記事は統合されるか、リダイレクトに置き換えられるか、さもなくば削除される可能性があります。出典検索?: 大野遥...

Paul Brown Datos personalesNacimiento Norwalk (Estados Unidos)7 de septiembre de 1908 Norwalk, OhioNacionalidad(es) EstadounidenseFallecimiento Cincinnati (Estados Unidos)5 de agosto de 1991Cincinnati, OhioCarrera deportivaDeporte Fútbol americanoEquipo universitario Miami (Ohio)Estado RetiradoClub profesionalDebut deportivo 1943Posición Entrenador en jefeDorsal(es) NingunoMarca de partidos ganados-perdidos 213-104-9% de partidos ganados .672Partidos 326Retirada deportiva 1975Trayectoria Co...

The Karate Kid 2Theatrical posterSutradaraHarald ZwartProduserJerry WeintraubWill SmithJada Pinkett SmithJames LassiterKen StovitzSkenarioChristopher MurpheyCeritaRobert Mark KamenPemeranJaden SmithJackie ChanWenwen HanTaraji P. HensonPenata musikJames HornerSinematograferRoger PrattPenyuntingKevin StermerPerusahaanproduksiOverbrook EntertainmentJW ProductionsChina Film GroupDistributorColumbia PicturesTanggal rilis 11 Juni 2010 (2010-06-11) Durasi140 Menit[1]NegaraAmerika ...