Histoire de la théorie des cordes
|
Read other articles:

Phenothrin Names IUPAC name (3-Phenoxyphenyl)methyl 2,2-dimethyl-3-(2-methylprop-1-enyl)cyclopropane-1-carboxylate Other names Sumithrin; Phenothrine; Phenoxythrin; Sumitrin; Wellcide; Pibutin; Anvil; Duet; Anchimanaito 20S Identifiers CAS Number 26002-80-2 Y 3D model (JSmol) Interactive image Beilstein Reference 2160930 ChEBI CHEBI:34916 Y ChEMBL ChEMBL1322884 Y ChemSpider 4603 Y DrugBank DB13717 ECHA InfoCard 100.043.079 EC Number 247-404-5 KEGG D08357 Y MeSH Phenot...

Bitter Tears redirects here. For other uses, see Bitter Tears (disambiguation). 1964 studio album by Johnny CashBitter Tears: Ballads of the American IndianStudio album by Johnny CashReleasedOctober 26, 1964RecordedMarch 5 – June 30, 1964Genre Country folk Length31:13LabelColumbiaProducer Don Law Frank Jones Johnny Cash chronology I Walk the Line(1964) Bitter Tears: Ballads of the American Indian(1964) Original Sun Sound of Johnny Cash(1964) Singles from Bitter Tears: B...

Se ha sugerido que esta página sea renombrada como «Judiones de La Granja». Motivo: aún no se han proporcionado motivos para el renombrado. Detalle del judión de La Granja Judiones de La Granja cocidos Judiones de la Granja en Real Sitio de San Ildefonso Se denomina judiones de La Granja a una variedad de judía de gran tamaño que se cultiva en el Real Sitio de San Ildefonso (provincia de Segovia, Castilla y León, España), la Phaseolus coccineus, también denominada Phaseolus multiflo...

Das Friedrich-Lueg-Haus in Bochum wurde als erstes Hochhaus Bochums überhaupt mit einer Höhe von 32 m vom Architekten Emil Pohle entworfen und von 1924 bis 1925 errichtet. Es markiert eine neue Bauweise in der Architekturgeschichte einer Stadt mit heute 360.000 Einwohnern. Lueg Haus, 2007 Auftraggeber war das Unternehmen Fahrzeug-Werke Lueg. Im Erdgeschoss befand sich ein Autosalon. Das bis heute Lueg-Haus genannte Gebäude war bei seiner Eröffnung das größte Ausstellungshaus Deutschland...

село Гайове Країна Україна Область Київська область Район Броварський Громада Великодимерська селищна громада Основні дані Засноване 1922 Колишня назва Фрунзівка Населення 102 Площа 5,7 км² Густота населення 17,89 осіб/км² Поштовий індекс 07431 Телефонний код +380 4594 Геог

La Primavera(Le Printemps) Año 1886Autor William-Adolphe BouguereauTécnica Pintura al óleoEstilo AcademicismoTamaño 201 cm × 117 cmLocalización Museo de Arte Joslyn, Nebraska, Estados UnidosPaís de origen Francia[editar datos en Wikidata] La Primavera (en francés: Le Printemps), también conocida como El Regreso de la Primavera, es una de las obras más conocidas de William-Adolphe Bouguereau; fue realizada en 1886 y es una representación de una ninfa al inicio de la ...

مدينة أبيي أبيي منظر لمدينة أبيي، مع المساكن التقليدية (2009). الاسم الرسمي Abyei الإحداثيات 9°35′44″N 28°26′13″E / 9.5955555555556°N 28.436944444444°E / 9.5955555555556; 28.436944444444 تقسيم إداري الدولة جنوب السودان السودان المنطقة الإدارية منطقة أبيي عاصمة لـ منطقة أبيي خصائص...

Sebuah ketopong Negau ditemukan di Situs arkeologi Hallstatt, dekat Vače, Slovenia. Ketopong ini sekarang disimpan di Museum Prasejarah dan Sejarah Awal (Berlin). Ketopong Negau adalah kumpulan dua puluh enam ketopong[a] yang diperkirakan dibuat pada tahun 450 SM–350 SM. Ketopong-ketopong tersebut ditemukan pada tahun 1812 di Ženjak, dekat Negau, Kadipaten Steiermark (kini Negova, Slovenia).[1] Ketopong tersebut berbentuk khas vetulonia daru Peradaban Etruria, kadang-kadan...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 41st Tharallah Division – news · newspapers · books · scholar · JSTOR (November 2016) (Learn how and when t...

Christof Breitsameter Christof Breitsameter (* 6. Juli 1967 in Bobingen) ist ein deutscher katholischer Theologe und Hochschullehrer. Er war von 2008 bis 2013 Professor für Moraltheologie an der Ruhr-Universität Bochum und folgte 2013 dem Ruf an die Westfälische Wilhelms-Universität Münster. Seit 2014 ist er Professor für Moraltheologie an der Katholisch-Theologischen Fakultät der Ludwig-Maximilians-Universität München. Inhaltsverzeichnis 1 Leben 2 Werke 3 Weblinks 4 Einzelnachweise ...
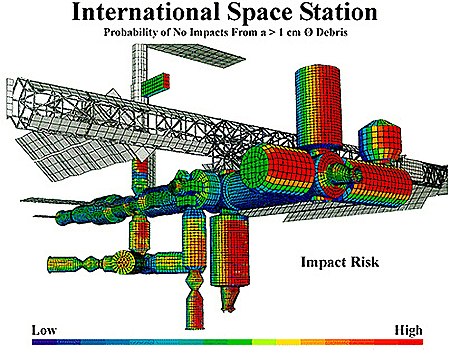
Identification, evaluation and control of risks For other uses, see Risk (disambiguation). For business risks, see Risk analysis (business). For the magazine, see Risk Management (magazine). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Risk management – news · newspapers · books · scholar · JSTOR (January...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2021) صمم سابق للنطق prelingual deafness معلومات عامة من أنواع صمم تعديل مصدري - تعديل الصمم السابق للنطق أو الصمم ما قبل اكتساب اللغة هو الصمم الذي يحدث قبل تعلم ال�...

Music merchandisers' trade show NAMMStatusActiveGenreMusic industryVenueAnaheim Convention CenterLocation(s)Anaheim, CaliforniaCountryUnited StatesInauguratedJanuary 1902; 121 years ago (1902-01)Most recentApril 13, 2023; 7 months ago (2023-04-13)Next eventJanuary 25, 2024; 49 days' time (2024-01-25)Attendance 46,711 (2023)[1]Organized byNAMM (National Association of Music Merchants)Filing status501(c)(6)Websitewww.namm.o...

Free and open-source video game LugaruDeveloper(s)Wolfire Games / David RosenInitial releaseMac OS XJanuary 28, 2005[1]WindowsMay 10, 2005LinuxAugust 26, 2005[2]Stable releaseLugaru HD / January 28, 2010 Repositoryhttps://gitlab.com/osslugaru/lugaruPlatformAmigaOS 4, AROS, Linux, Microsoft Windows, Mac OS XTypeSingle-player, actionLicenseGPL, CC BY-SA 3.0Websitewww.wolfire.com/lugaru Lugaru: The Rabbit's Foot is the first commercial video game created by indie developer ...

Pour les articles homonymes, voir Daybreak (homonymie). Cet article est une ébauche concernant une entreprise liée au jeu vidéo. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Les entreprises étant sujettes à controverse, n’oubliez pas d’indiquer dans l’article les critères les rendant admissibles. Daybreak Game Company Création 1998 (Sony Online Entertainment)2015 Dates clés mai 2000 (rachat de Verant Int.)février 2015 (rachat par Columbus Nova) fi...

Agreement to engage in illegal activity Contract law Formation Capacity Offer and acceptance Meeting of the minds2 Abstraction principle4,5 Posting rule1 Mirror image rule Invitation to treat Firm offer Consideration1,4 Implication-in-fact Collateral contract Defences Misrepresentation Mistake Threats and unequal bargaining power Illegality and public policy Unconscionability Culpa in contrahendo2 Force majeure Frustration of purpose Impossibility Impracticability Hardship Set-off Illusory pr...

Eurovision Song Contest 2006Country SloveniaNational selectionSelection processEMA 2006Selection date(s)29 January 2006Selected entrantAnžej DežanSelected songMr NobodySelected songwriter(s)Matjaž VlašičUrša VlašičFinals performanceSemi-final resultFailed to qualify (16th)Slovenia in the Eurovision Song Contest ◄2005 • 2006 • 2007► Slovenia participated in the Eurovision Song Contest 2006 with the song Mr Nobody written by Urša Vlašić and ...

1st century High Priest of Israel (d. 68 CE) This article needs more complete citations for verification. Please help add missing citation information so that sources are clearly identifiable. (August 2017) (Learn how and when to remove this template message) Ananus ben AnanusTitleHead of Judean provisional governmentPersonalBornRoman JudeaDied68Jerusalem, Roman JudeaReligionJudaismLineageson of AnnasSectSadduceeOther namesHanan ben Hanan, Ananus ben ArtanusTempleTemple of JerusalemJewis...

Juan Surraco Nazionalità Uruguay Altezza 176 cm Peso 69 kg Calcio Ruolo Attaccante Termine carriera 2021 Carriera Giovanili 2003-2005 Central Español Squadre di club1 2005-2006 Central Español12 (1)2006-2007 Udinese0 (0)2007-2008→ Messina24 (0)2008-2010→ Ancona71 (5)[1]2010-2011→ Livorno25 (6)2011-2012→ Torino23 (1)2012-2014 Modena33 (2)2014 Cittadella18 (2)2014-2015 Livorno4 (0)2015 El Tanque Sisley7 (0)2015-...

1995 single by No Doubt This article is about the 1995 song. For other uses, see Spider Web (disambiguation). SpiderwebsCover art for UK CD singleSingle by No Doubtfrom the album Tragic Kingdom ReleasedNovember 19, 1995Recorded1994GenreSka punk[1][2]new wavepop-punkalternative rock[3]Reggae[4]Length 4:28 3:50 (radio edit) LabelInterscopeTraumaSongwriter(s)Gwen StefaniTony KanalProducer(s)Matthew WilderNo Doubt singles chronology Just a Girl (1995) Spiderwebs (1...









