Harmonie des sphères
|
Read other articles:

Prapañcaꦩ꧀ꦥꦸꦥꦿꦥꦚ꧀ꦕLahirDhang Acarya Nadendra MajapahitKebangsaan MajapahitNama lainWinada, Empu Prapañca, Mpu PrapancaPekerjaanPenulisPendeta BuddhaDharmadyaksa KasogatanKarya terkenalKakawin Nāgarakṛtâgama (1365) Empu Prapañca (disebut juga Dang Acarya Nadendra) adalah nama samaran dari pujangga sastra Jawa yang hidup pada abad ke-14 pada zaman Majapahit dan kemungkinan selain pujangga juga merupakan mpu yang paling ternama pada masanya. Namanya dikenal di In...

Halaman ini berisi artikel tentang permainan video. Untuk karakternya, lihat Pac-Man (karakter). Pac-Man Publikasi 22 Mei 1980 Genremaze video game (en) KarakterPac-Man (karakter) Bagian dariNamco Museum Virtual Arcade (en) Karakteristik teknisSistem operasiAndroid dan iOS PlatformGame Boy Advance, Windows Phone, Android, Atari 5200, Commodore VIC-20, Atari 2600, MSX, Commodore 64, Sega Game Gear, Linux, Windows, ZX Spectrum, Xbox 360, Amiga, DOS, Nintendo Entertainment System, Super Nintendo...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Questa voce o sezione sull'argomento architettura è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i suggerimenti del progetto di riferimento. Coordinate: 41°54′11.34″N 12°28′2...

2005 single by EditorsMunichCover of the original single from 2005Single by Editorsfrom the album The Back Room B-side Disappear Crawl Down the Wall Colours Release Camera French Disko Find Yourself a Safe Place Released18 April 2005 (2005-04-18)Recorded2005Genre Post-punk revival indie rock Length3:46LabelKitchenwareSongwriter(s) Edward Lay Russell Leetch Tom Smith Chris Urbanowicz Producer(s)Jim AbbissEditors singles chronology Bullets (2005) Munich (2005) Blood (2005) 2006 R...

J.H. Binford Peay IIIGeneral James Henry Binford Peay IIINickname(s)BinnieBorn (1940-05-10) May 10, 1940 (age 83)Richmond, Virginia, U.S.AllegianceUnited StatesService/branchUnited States ArmyYears of service1962–1997RankGeneralCommands heldUnited States Central CommandVice Chief of Staff of the United States Army101st Airborne Division2d Battalion, 11th Field Artillery RegimentBattles/warsVietnam WarGulf WarAwardsDefense Distinguished Service MedalArmy Distinguished Service Meda...

جائزة مدينة مكسيكو الكبرى 2022 السباق 20 من أصل 22. السلسلة بطولة العالم لسباقات فورمولا 1 موسم 2022 البلد المكسيك التاريخ بداية:28 أكتوبر 2022 نهاية:30 أكتوبر 2022 مكان التنظيم حلبة هيرمانوس رودريغيز طول المسار 4.304 كيلومتر (2.674 ميل) المسافة 305.354 كيلومتر، (189.738 ميل) عدد اللفا...

Majalah Billboard menyusun tangga lagu nasional Indonesia berjudul Indonesia Songs (Indonesia: Lagu-Lagu Indonesiacode: id is deprecated ) sejak Februari 2022, menggantikan Billboard Indonesia Top 100. Berbeda dengan tangga lagu terdahulu, Indonesia Songs tidak hanya memeringkatkan lagu-lagu dari artis Indonesia, namun juga mencakup lagu-lagu dari artis mancanegara. Tangga lagu ini meliputi 25 singel paling populer secara nasional dalam kurun waktu satu minggu berdasarkan data streaming dan ...

Architecture of the U.S. state of Texas The architecture of the U.S. state of Texas comes from a wide variety of sources. Many of the state's buildings reflect Texas' Spanish and Mexican roots; in addition, there is considerable influence from mostly the American South as well as the Southwest. Rapid economic growth since the mid twentieth century has led to a wide variety of contemporary architectural buildings. Traditional architecture Main article: Spanish missions in TexasThe Alamo The fi...

Basilica minore di Sant'Agnese fuori le muraLa facciata della basilicaStato Italia RegioneLazio LocalitàRoma IndirizzoVia Nomentana, 349, 00162 Roma RM Coordinate41°55′22.58″N 12°31′07.75″E / 41.92294°N 12.51882°E41.92294; 12.51882Coordinate: 41°55′22.58″N 12°31′07.75″E / 41.92294°N 12.51882°E41.92294; 12.51882 Religionecattolica di rito romano TitolareSant'Agnese martire OrdineCanonici Regolari del Santissimo Salvatore Lateranense...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

American college basketball season 2005–06 LSU Tigers basketballSEC regular season championsNCAA tournament, Final FourConferenceSoutheastern ConferenceRankingCoachesNo. 3APNo. 19Record27–9 (14–2 SEC)Head coachJohn Brady (9th season)Home arenaPete Maravich Assembly CenterSeasons← 2004–052006–07 → 2005–06 Southeastern Conference men's basketball standings vte Conf Overall Team W L PCT W L PCT East No. 18 ...

Sacred GroundSingle by Kix Brooksfrom the album Kix Brooks B-sideThe Story of My LifeReleased1989GenreCountryLength2:51LabelCapitol Nashville 44275Songwriter(s)Kix Brooks, Vernon RustProducer(s)Rafe Van HoyKix BrooksKix Brooks singles chronology I'm on to You (1988) Sacred Ground (1989) She Does the Walk on By (1989) Sacred Ground is a country music song, co-written and originally recorded by American country music singer Kix Brooks, prior to his joining Ronnie Dunn in the duo Brooks & Du...

Questa voce sull'argomento ciclisti belgi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Kenny De KeteleNazionalità Belgio Altezza178 cm Peso66 kg Ciclismo SpecialitàPista, strada Termine carriera2021 CarrieraSquadre di club 2004Jong Vlaanderen 20162005-2006Bodysol-Win for Life2007Davitamon-Win for Life2007 Chocolade Jacques2008-2016 Topsport Vlaand.2017-2021 Sport Vlaanderen Nazionale 2007-2021 Belgiopista Palmarès Mondi...

Возрастно-половая пирамида населения Восточного Тимора на 2020 год Население Восточного Тимора составляет 1 066 409 человек[1] (2010, перепись). Содержание 1 Этнический состав 1.1 Расовый тип 2 Языки 3 Религии 4 Примечания 5 Литература Этнический состав Коренное население не пре...

Metro station in Ansan, South Korea 448 상록수 (안산대학교)Sangnoksu(Ansan Univ.) Korean nameHangul상록수역Hanja常綠樹驛Revised RomanizationSangnoksu-yeokMcCune–ReischauerSangnoksu-yŏk General informationLocation409 Bono-dong, 61 Sangnoksuro, Sangnok-gu, Ansan-si, Gyeonggi-do[1]Operated byKorailLine(s) Line 4Platforms2Tracks4ConstructionStructure typeAbovegroundKey datesOctober 25, 1988[1] Line 4 open...

Disambiguazione – Se stai cercando il sistema di scrittura della lingua latina, vedi Scrittura e pronuncia del latino. Storia dell'alfabeto Media età del bronzo XIX secolo a.C. Ugaritico XV secolo a.C. Proto-cananeo XV secolo a.C. Fenicio XIV–XI secolo a.C. Paleo-ebraico X secolo a.C. Samaritano VI secolo a.C. Aramaico VIII secolo a.C. Brāhmī VI secolo a.C. Devanāgarī VIII secolo d.C. Tibetano VII secolo d.C. Khmer/giavanese IX secolo d.C. Ebraico III secolo a.C. Siriaco II secolo a...

Questa voce o sezione sull'argomento vescovi italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Carlo Emanuele Sardagna von Hohensteinarcivescovo della Chiesa cattolica Nato20 marzo 1772 a Trento Ordinato presbitero7 dicembre 1797 Nominato vescovo28 febbraio 1831 da papa Gregorio XVI Consacrat...

للفترة السابقة التي كانت تُعرف باسم «جمهورية فنزويلا» من 1953 إلى 1999، انظر جمهورية فنزويلا لمعانٍ أخرى، طالع فنزويلا (توضيح). فنزويلا (بالإسبانية: República Bolivariana de Venezuela) فنزويلاعلم فنزويلا فنزويلاشعار فنزويلا النشيد: المجد للشعب الشجاع الأرض وا...
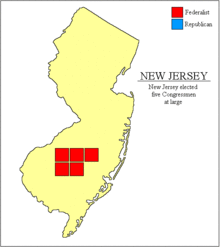
Elections in New Jersey Federal government U.S. President 1788-89 1792 1796 1800 1804 1808 1812 1816 1820 1824 1828 1832 1836 1840 1844 1848 1852 1856 1860 1864 1868 1872 1876 1880 1884 1888 1892 1896 1900 1904 1908 1912 1916 1920 1924 1928 1932 1936 1940 1944 1948 1952 1956 1960 1964 1968 1972 1976 1980 1984 1988 1992 1996 2000 2004 Dem 2008 Rep Dem 2012 2016 Dem 2020 Dem 2024 Rep U.S. Senate 1788 1790 1790 (sp) 1792 1796 1796 (sp) 1798 1799 (sp) 1801 (sp) 1803 (sp) 1804 1808 1809 1809 (sp)...
