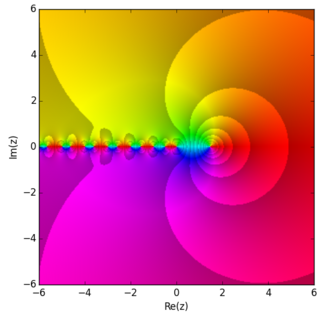
Fonction digamma
|
Read other articles:

Keling-peri sisik-merah Cirrhilabrus rubrisquamis Cirrhilabrus rubrisquamis (male in circular close-up, females marked by white arrows) and anthiasStatus konservasiKekurangan dataIUCN187581 TaksonomiKerajaanAnimaliaFilumChordataKelasActinopteriOrdoPerciformesFamiliLabridaeGenusCirrhilabrusSpesiesCirrhilabrus rubrisquamis Randall, 1983 lbs Ikan Keling-peri sisik-merah ( Cirrhilabrus rubrisquamis ), juga dikenal sebagai keling-peri beludru merah, adalah spesies ikan wrasse yang berasal dari Kep...

Atol NoonuNegaraMaladewaAtol-atol terkaitMiladhunmadulu DhekunuburiLokasi5°58' N and 5°38' NIbukotaManadhooPemerintahan • Kepala AtolFaruhath Ali [1]Populasi • Total14.502Kode posDKode pos DhivehiN (ނ)• Jumlah pulau71• Pulau berpenghuniFoddhoo, Henbandhoo, Holhudhoo, Kendhikolhudhoo, Kudafaree, Landhoo, Lhohi, Maafaru, Maalhendhoo, Magoodhoo, Manadhoo, Miladhoo, Velidhoo• Pulau tidak berpenghuniBadadhidhdhoo, Bodufushi, Bodulhaimendhoo, Bomasdhoo, Burehifasdho...
Masakini MasakituGenreGaya hidupPresenterHideki FujiwaraHaruka NakagawaNegara asalIndonesiaBahasa asliBahasa IndonesiaProduksiDurasi30 menitRumah produksiNET. LifestyleDistributorNet Visi MediaRilis asliJaringanFormat gambarHDTV (1080i 16:9)Format audioDolby Digital 5.1Rilis5 November 2022 (2022-11-05) –19 Februari 2023 (2023-2-19)Acara terkaitQueen at Home Chef's Table Masak Enak Masak Asik Masak Masak, Kuali Barbar (Trans TV) Cemplang Cemplung, Mendadak Chef, Juru Masak Ci...

Loose group of white nationalist activists, provocateurs, and internet trolls For the cartoon after which the group is named, see Pepe the Frog § Groyper. Groypers Groyper meme, the namesake of the groupKey figures Nick Fuentes Michelle Malkin Baked Alaska Jaden McNeil Ideology American nationalism[1] Antisemitism[1] Anti-Zionism[1] Christian right[1] Paleoconservatism[2] White nationalism[1] Political positionFar-rightAffiliations Am...

Lithuanian cyclist (born 1982) Simona KrupeckaitėKrupeckaitė at the 2015 UEC European Track ChampionshipsPersonal informationBorn (1982-12-13) 13 December 1982 (age 41)Utena,Height1.70 m (5 ft 7 in)[1]Weight65 kg (143 lb)[1]Team informationDisciplineTrack cyclingRoleRiderRider typeSprinterProfessional teams2004–2005Aliverti-Bianchi-Kookai2007–2009Safi-Pasta Zara-Manhattan Major wins Two world records holder* 3× Lithuanian Sportsperson ...

Sniper rifle Dan IWI Dan at IDEX 2023TypeSniper riflePlace of origin IsraelProduction historyDesignerNehemia SirkisManufacturerIsrael Weapon IndustriesProduced2014–presentSpecificationsMass5.9 kg (13.01 lb) 7.3 kg (16 lb) folding stock versionLength1,280 mm (50.4 in) 1,030 mm (40.6 in) stock foldedBarrel length737 mm (29.0 in)Cartridge.338 Lapua MagnumActionBolt-actionMuzzle velocity881 m/s (2,890 ft/s)Effe...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2016. World Fuel Services CorporationJenispublik (NYSE: INTL)IndustriEnergiKantorpusatMiami, Florida, Amerika SerikatWilayah operasiSeluruh duniaTokohkunciMichael J. Kasbar(CEO)Situs webwww.wfscorp.com World Fuel Services Corporation (NYSE: INTL) adalah sebuah...

Wilderness area in Arizona and Utah, U.S. Paria Canyon-Vermilion Cliffs WildernessIUCN category Ib (wilderness area)LocationCoconino County, Arizona / Kane County, Utah, United StatesNearest cityPage, ArizonaCoordinates36°53′46″N 111°49′37″W / 36.8960968°N 111.8268367°W / 36.8960968; -111.8268367[1]Area112,500 acres (455 km2)[2]EstablishedAugust 28, 1984Governing bodyU.S. Bureau of Land Management The Paria Canyon-Vermilion Cl...

Election in South Carolina Main article: 1972 United States presidential election 1972 United States presidential election in South Carolina ← 1968 November 7, 1972 1976 → Nominee Richard Nixon George McGovern Party Republican DemocraticUnited Citizen [a] Home state California South Dakota Running mate Spiro Agnew Sargent Shriver Electoral vote 8 0 Popular vote 478,427 189,270 Percentage 70.58% 27.92% County Results Nixon 50-...

تحتاج هذه المقالة كاملةً أو أجزاءً منها إلى تدقيق لغوي أو نحوي. فضلًا ساهم في تحسينها من خلال الصيانة اللغوية والنحوية المناسبة. (أبريل 2020) ماريا فان كيروف معلومات شخصية اسم الولادة (بالإنجليزية: Maria Rosanne DeJoseph) الميلاد 20 فبراير 1977 (47 سنة) نيو هارتفورد الإقامة جنيفك�...

Lutold de ZnojmoTitre de noblesseMargraveBiographieDécès 15 mars 1112ZnaïmNom dans la langue maternelle LitoldFamille PřemyslidesPère Conrad Ier de BohêmeMère Wilpirk de Tenling (en)Fratrie Ulrich IerConjoint Ida de Babemberg (d)Enfants Naděj Spes (d) (?)Conrad II de Znojmomodifier - modifier le code - modifier Wikidata Luitpold de Znojmo (tchèque : Litold znojemský, allemand : Luitpold von Znaim, latin : Lutoldus Znoyemsis; mort le 15 mars[notes 1] 111...

Dahui Zonggao Informasi pribadiLahir1089TiongkokMeninggal10 Agustus 1163 (usia 73-74)AgamaAgama BuddhaMazhabLinjiKedudukan seniorPendahuluYuanwu Keqin Dahui Zonggao (1089–10 Agustus 1163) (Hanzi: 大慧宗杲; Wade–Giles: Ta-hui Tsung-kao; Jepang: Daie Sōkō; Vietnam: Đại Huệ Tông Cảo) adalah seorang mahaguru Chan (Zen) Tiongkok. Dahui adalah murid dari Yuanwu Keqin (Wade–Giles: Yuan-wu K'o-ch'in; Jepang: Engo Kokugon) (1063–1135) dan generasi ke-12 dari mazhab Linji ...

Peta infrastruktur dan tata guna lahan di Komune Le Châtelet-en-Brie. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiLe Châtelet-en-BrieNegaraPrancisArondisemenMelunKantonLe Châtelet-en-BrieAntarkomuneCommunauté de communes de la Région du Châtelet-en-BriePemerintahan • Wali kota (2008-2014) Alain Mazard • Populasi14.532Kode INSEE/pos...

Азиатский барсук Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКласс:Мле�...

Pour les articles homonymes, voir Bell. Johannes Bell Johannes Bell en 1908. Fonctions Ministre du Reich à la Justice 16 mai – 17 décembre 1926(7 mois et 1 jour) Chancelier Wilhelm Marx Gouvernement Marx III Prédécesseur Wilhelm Marx Successeur Oskar Hergt Ministre des Transports 13 février 1919 – 1er mai 1920(1 an, 2 mois et 18 jours) Chancelier Philipp ScheidemannGustav BauerHermann Müller Gouvernement ScheidemannMüller I Prédécesseur Début de la Rép...

Alfa Romeo Giulia è stata la prima vettura ad adottare il pianale Giorgio La piattaforma Alfa Romeo Giorgio è un pianale, progettata dalla Alfa Romeo insieme alla Fiat Chrysler Automobiles nel 2013[1] e utilizzata a partire dal 2016. Sostituisce il pianale premium dell'Alfa Romeo. Indice 1 Descrizione 2 Veicoli basati sulla piattaforma 3 Note 4 Altri progetti Descrizione Il costo per lo sviluppo e la realizzazione è stato di circa un miliardo di euro.[2][3][4 ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2019) طواف سويسرا 1997تفاصيل السباقسلسلة61. طواف سويسراالتواريخ17 – 26 يونيو 1997المسافات1٬513 كمالبلد سويسرانقطة ال�...
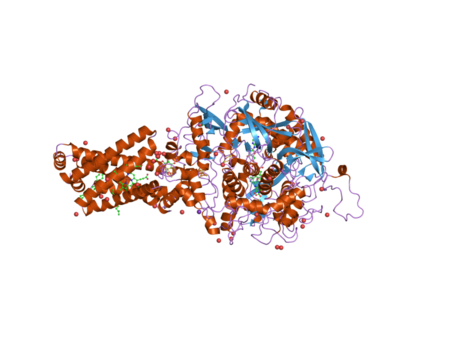
SDHBPengidentifikasiAliasSDHB, CWS2, IP, PGL4, SDH, SDH1, SDH2, SDHIP, succinate dehydrogenase complex iron sulfur subunit B, MC2DN4ID eksternalOMIM: 185470 MGI: 1914930 HomoloGene: 2255 GeneCards: SDHB Ontologi genFungsi molekuler• ubiquinone binding• iron-sulfur cluster binding• metal ion binding• succinate dehydrogenase (ubiquinone) activity• GO:0001948, GO:0016582 Ikatan protein plasma• oxidoreductase activity• electron transfer activity• 2 iron, 2 sulfur cluster bind...

Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. PolmoniteQuadro radiografico di polmonite nel lobo superiore sinistro (le frecce indicano i confini tra lobo inferiore e superiore)Specialitàpneumologia e infettivologia Eziologiainfezione, polmonite ab ingestis e fumare Classificazione e risorse esterne (EN)ICD-9-CM480, 481, 482, 483, 484, 485, 486 e 770.0 I...

Rugby teamSan FranciscoFull nameSan Francisco Golden Gate Rugby Football ClubUnionUSA RugbyNickname(s)SFGGFounded2001; 23 years ago (2001)Ground(s)Ray Sheeran FieldPresidentPaul SantinelliCoach(es)Neil FooteLeague(s)Pacific Rugby Premiership Team kit Official websitesfggrugby.sportsengine-prelive.com San Francisco Golden Gate Rugby Football Club is a rugby union club based in San Francisco, California. SFGG's first side competes in the Northern California Rugby Football Unio...