Concentration de mesure
|
Read other articles:

Edison Flores Edison Flores Ekuador vs Peru 2017Informasi pribadiNama lengkap Edison FloresTanggal lahir 14 Mei 1994 (umur 29)Tempat lahir Lima, PeruTinggi 170 cm (5 ft 7 in)Posisi bermain GelandangInformasi klubKlub saat ini AalborgNomor 10Karier senior*Tahun Tim Tampil (Gol)2016 – Aalborg 35 (2)Tim nasional2013 – Peru 33 (9) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Edison Flores (lahir 14 Mei 1994) adalah seorang pemain sepak bola berkew...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Jesiel Cardoso MirandaInformasi pribadiNama lengkap Jesiel Cardoso MirandaTanggal lahir 5 Maret 1994 (umur 30)Tempat lahir BrasilTinggi 1,86 m (6 ft 1 in)Posisi bermain BekInformasi klubKlub saat ini Kawasaki FrontaleKarier senior*...

العلاقات الأذربيجانية الموريتانية أذربيجان موريتانيا أذربيجان موريتانيا تعديل مصدري - تعديل العلاقات الأذربيجانية الموريتانية هي العلاقات الثنائية التي تجمع بين أذربيجان وموريتانيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومر...

1961 New Jersey gubernatorial election ← 1957 November 7, 1961 1965 → Nominee Richard J. Hughes James P. Mitchell Party Democratic Republican Popular vote 1,084,194 1,049,274 Percentage 50.4% 48.7% County resultsHughes: 50–60% 60–70% Mitchell: 50–60% 60–70% Governor before election Robert B. Meyner Democratic Elected Governor Richar...

Sports season2022–23 American Athletic Conference men's basketball seasonLeagueNCAA Division ISportBasketballDurationNovember 2022through March 2023Number of teams11TV partner(s)CBS, ESPN, ESPN+Regular seasonSeason championsHoustonSeason MVPMarcus Sasser, HoustonTournamentChampionsMemphis Runners-upHoustonAmerican Athletic Conference men's basketball seasons← 2021–222023–24 → 2022–23 American Athletic Conference men's basketball standings vte Conf Overall Tea...

English footballer For other people named Paul Jones, see Paul Jones (disambiguation). Paul Jones Jones playing for Barrow in 2008Personal informationFull name Paul JonesDate of birth (1978-06-03) 3 June 1978 (age 45)Place of birth Liverpool, EnglandPosition(s) DefenderTeam informationCurrent team MarineYouth career??–1996 Tranmere RoversSenior career*Years Team Apps (Gls)1996–1997 Tranmere Rovers 0 (0)1997 → Blackpool (loan) 0 (0)1997–1999 Barrow 87 (3)1999 Leigh RMI ? (?)1999�...

24°41′42″N 84°59′29″E / 24.695102°N 84.991275°E / 24.695102; 84.991275 Bodh Gaya Bodh Gaya Negara Bagian - Distrik Bihar - Gaya Koordinat 24°41′42″N 84°59′29″E / 24.695102°N 84.991275°E / 24.695102; 84.991275 Luas Zona waktu IST (UTC+5:30) Populasi (2001) - Kepadatan 30,883 - Ziarah keTempat-tempat suciBuddhisme Empat Tempat Utama Lumbinī Buddhagayā Isipatana Kusinārā Empa...

Перуанский анчоус Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые �...
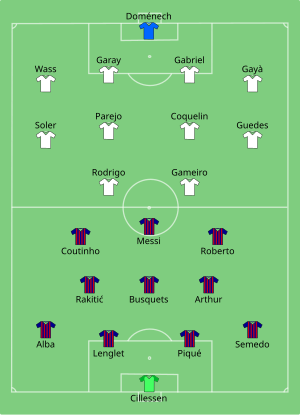
Football match2019 Copa del Rey finalThe Estadio Benito Villamarín prior to the finalEvent2018–19 Copa del Rey Barcelona Valencia 1 2 Date25 May 2019 (2019-05-25)VenueBenito Villamarín, SevilleRefereeAlberto Undiano MallencoAttendance53,698← 2018 2020 → The 2019 Copa del Rey final was a football match played on 25 May 2019 that decided the winner of the 2018–19 Copa del Rey, the 117th edition of Spain's primary football cup (including two seasons where two ri...

John Anderson, 1st Viscount Waverley John Anderson, 1st Viscount Waverley, GCB, OM, GCSI, GCIE, PC, PC (Ire), FRS[1] (8 Juli 1882 – 4 Januari 1958) adalah seorang pegawai negeri dan politikus asal Inggris. Ia dikenal karena menjabat dalam Kabinet pada Perang Dunia Kedua. Referensi ^ Bridges, L.; Dale, H. (1958). John Anderson, Viscount Waverley 1882-1958. Biographical Memoirs of Fellows of the Royal Society. 4: 306. doi:1...

Swiss cyclist Paul ZollingerPersonal informationBorn (1944-03-10) 10 March 1944 (age 80)Schlieren, SwitzerlandTeam informationDisciplineRoadRoleRiderProfessional teams1966–1968Tigra–Meltina1968Frimatic–Wolber–de Gribaldy Paul Zollinger (born 10 March 1944) is a Swiss former racing cyclist. He was the Swiss National Road Race champion in 1966.[1] His twin brother Rudi was also a professional cyclist. Major results 1966 1st Road race, National Road Championships 7th Overall...

Chemical compound SaxagliptinClinical dataTrade namesOnglyzaOther namesBMS-477118AHFS/Drugs.comProfessional Drug FactsMedlinePlusa610003License data EU EMA: by INN US DailyMed: Saxagliptin US FDA: Saxagliptin Pregnancycategory AU: B3 Routes ofadministrationBy mouth (tablets)Drug classDPP-4 inhibitorsATC codeA10BH03 (WHO) Legal statusLegal status AU: S4 (Prescription only) UK: POM (Prescription only) US: ℞-only EU: Rx-only Phar...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. SMPN 20 BatamInformasiJenisSekolah NegeriAlamatLokasiTiban Koperasi, Batam, Kepri, IndonesiaMoto SMPN 20 Batam, merupakan salah satu Sekolah Menengah Pertama Negeri yang ada di Provinsi Kepulauan Riau, yang beralamat di Tiban Koperasi - Batam. Sa...

Castle in East Azerbaijan Province, Iran For other places with similar names, see Naryn castle. Naryn Castleنارین قلعهGeneral informationTypeCastleTown or citySardrudCountry IranNaryn Castle (Persian: نارین قلعه) is a historical castle located in Tabriz County in East Azerbaijan Province, The longevity of this fortress dates back to the 1st millennium BC.[1][2] References ^ پرونده ثبتی نارین قلعه سردرود در حال بررسی است. ...

拉尔·巴哈杜尔·夏斯特里第二任印度总理任期1964年6月9日—1966年1月11日总统薩瓦帕利·拉達克里希南前任古爾扎里拉爾·南達继任古爾扎里拉爾·南達印度外交部長任期1964年6月9日—1964年7月18日总理自己前任古爾扎里拉爾·南達继任斯瓦倫·辛格(英语:Swaran Singh)印度內政部長任期1961年4月4日—1963年8月29日总理賈瓦哈拉爾·尼赫魯前任戈文德·巴拉布·潘特(英语:Govind Balla...

Ethnic group in the Republic of Turkey Ethnic group Turkish SerbsСрби у ТурскојSrbi u Turskoj Total population165,401 (1965)[1]Regions with significant populationsIstanbul, GallipoliLanguagesTurkish and SerbianReligionSunni Islam, minority Serbian Orthodox Christian Part of a series onSerbs Native Serbia Vojvodina Kosovo and Metohija Bosnia and Herzegovina Montenegro Croatia North Macedonia Romania Hungary Albania Bulgaria Slovenia DiasporaEurope Austria Azerbaijan Belaru...

بيني أندرسون (بالسويدية: Benny Andersson) معلومات شخصية اسم الولادة (بالسويدية: Göran Bror Benny Andersson) الميلاد 16 ديسمبر 1946 (78 سنة)[1] ستوكهولم مواطنة السويد عضو في آبا الزوجة آني فريد لينغستاد (ز.1978-ط.1981)منى نوركلت (ز.1981) الأولاد 3 الحياة الفنية النوع روك، وب...
Variety of the Persian language spoken in Afghanistan For other uses, see Dari (disambiguation). DariAfghan Persian, Eastern PersianدریDari in Perso-Arabic script(Nastaʿlīq style)Pronunciation[d̪ɐˈɾiː]Native toAfghanistanSpeakersL1: 10 million (2017)[1]L2: 21 million (2022)[1]Language familyIndo-European Indo-IranianIranianWestern IranianSouthwestern IranianPersianDariDialects South-Eastern Hazaragi Western Sistani [note 1][2][3&...

Guillaume ErnerBiographieNaissance 8 février 1968 (56 ans)ParisNationalité françaiseFormation Université Paris-Sorbonne (doctorat) (jusqu'en 2002)Activités Journaliste, animateur de radio, sociologue, chroniqueur de presseConjoint Marie de GandtEnfant Alma Erner, Tadzio Erner, Côme ErnerAutres informationsA travaillé pour Institut d'études politiques de ParisCharlie HebdoFrance CultureFrance InterPublic SénatDirecteur de thèse Raymond Boudonmodifier - modifier le code - modifie...

El Chavo del OchoShow logo written in Glaser Babyteeth scriptNama alternatifEl Chavo del Ocho (1973–1975)Genre Sitcom Comedy Slapstick PembuatRoberto Gómez BolañosDitulis oleh Roberto Gómez Bolaños Francisco Gómez Bolaños Sutradara Enrique Segoviano Roberto Gómez Bolaños Pemeran Roberto Gómez Bolaños María Antonieta de las Nieves Carlos Villagrán Ramón Valdés Florinda Meza Rubén Aguirre Édgar Vivar Angelines Fernández Horacio Gómez Bolaños Raúl 'Chato' Padilla Penggubah...














































