Calcul fonctionnel matriciel
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Lamban...

Filsafat pendidikan merupakan ilmu filsafat yang mempelajari hakikat pelaksanaan dan pendidikan.[1] Bahan yang dipelajari meliputi tujuan, latar belakang, cara, hasil, dan hakikat pendidikan.[1] Metode yang dilakukan yaitu dengan analisis secara kritis struktur dan manfaat pendidikan.[1] Filsafat pendidikan berupaya untuk memikirkan permasalahan pendidikan.[2] Salah satu yang dikritisi secara konkret adalah relasi antara pendidik dan peserta didik dalam pembela...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Daftar pemusik Indonesia – berita · surat kabar · buku · cendekiawan · JSTORDaftar Musisi Indonesia adalah daftar yang berisi nama tokoh-tokoh musik dari Indonesia. Daftar ini belum lengkap, para pembaca...

Structural phenolic polymer in plant cell walls This article is about the wood polymer. For the phytoestrogen, see Lignan. Idealized structure of lignin from a softwood Lignin is a class of complex organic polymers that form key structural materials in the support tissues of most plants.[1] Lignins are particularly important in the formation of cell walls, especially in wood and bark, because they lend rigidity and do not rot easily. Chemically, lignins are polymers made by cross-link...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Associazione Sportiva Lucchese Libertas 1905. Unione Sportiva Lucchese LibertasStagione 1941-1942Sport calcio Squadra Lucchese Allenatore Renato Bodini Presidente Bruno Carletti Serie B18º posto. Retrocessa in Serie C. Coppa ItaliaSedicesimi di finale Maggiori p...

Australian rules footballer, born 1969 Australian rules footballer Michael LongOAM Long on The Long Walk in 2014Personal informationFull name Michael LongDate of birth (1969-10-01) 1 October 1969 (age 54)[1]Place of birth Tiwi IslandsOriginal team(s) St Mary's/West TorrensDraft No. 23., 1988 national draftHeight 178 cm (5 ft 10 in)Weight 82 kg (181 lb)Position(s) MidfielderPlaying career1Years Club Games (Goals)1988 West Torrens 022 0(11)1989–2001 ...

Эта статья или раздел нуждается в переработке.Пожалуйста, улучшите статью в соответствии с правилами написания статей. Мой шумный домангл. The Loud House Жанры комедийныйМультсериал Техники анимации компьютерная рисованная анимация (1—3 сезоны)flash-анимация (с 4 сезона) Созд�...

Jaimee Fourlis Jaimee Fourlis nel 2023 Nazionalità Australia Tennis Carriera Singolare1 Vittorie/sconfitte 197 - 145 (57.6%) Titoli vinti 0 WTA, 8 ITF Miglior ranking 147ª (18 luglio 2022) Ranking attuale ranking Risultati nei tornei del Grande Slam Australian Open 2T (2017) Roland Garros 1T (2017) Wimbledon 1T (2022) US Open 1T (2022) Doppio1 Vittorie/sconfitte 78 - 59 (56.93%) Titoli vinti 0 WTA, 6 ITF Miglior ranking 138ª (2 marzo 2020) Ranking attuale ran...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) دوري السوبر الألباني 2003–04 تفاصيل الموسم دوري السوبر الألباني النسخة 65 البلد ألبانيا التاريخ ب...

Mountain range in the US states of Texas and New Mexico For the smaller range in the southwest New Mexico Bootheel, see Guadalupe Mountains (Hidalgo County). For the mountain range in Extremadura, Spain, see Sierra de Villuercas. Guadalupe MountainsGuadalupe MountainsHighest pointPeakGuadalupe PeakElevation8,751 ft (2,667 m)Coordinates31°53′28″N 104°51′36″W / 31.89111°N 104.86000°W / 31.89111; -104.86000DimensionsLength65 mi (105 km...

Bilateral relationsAustralia-Italy relations Australia Italy Australia and Italy established formal diplomatic relations in 1949.[1] Francesca Tardioli was appointed Italian ambassador to Australia in September 2019, the first woman to represent Italy in Australia until her death in February 2022. The headquarters of the Italian embassy, designed by the Italian-Australian architect Enrico Taglietti, is located in the Canberra district of Deakin.[2] Margaret Twomey was appoint...

Vous lisez un « bon article » labellisé en 2023. Pour les articles homonymes, voir Le Grand Restaurant. Le Grand Restaurant Logo du film. Données clés Réalisation Jacques Besnard Scénario Jean HalainLouis de FunèsJacques BesnardJean Marion (non crédité) Musique Jean Marion Acteurs principaux Louis de FunèsBernard Blier Sociétés de production Gaumont Pays de production France Genre Comédie Durée 86 minutes Sortie 1966 Pour plus de détails, voir Fiche technique e...

State Recreation Site in Oregon, United States Agate Beach State Recreation SiteAlong a path leading to the beachShow map of OregonShow map of the United StatesTypePublic, stateLocationLincoln County, OregonNearest cityNewport, Oregon, United StatesCoordinates44°39′31″N 124°03′29″W / 44.6587278°N 124.0581726°W / 44.6587278; -124.0581726[1]Area18.48 acres (7.48 ha)Elevation16 feet (5 m)Created1969Operated byOregon Parks and Recrea...

Cable car station at Jardim da Flora Cable car gondola lift The Guia Hill Cable Car (Chinese: 松山纜車; Portuguese: Teleférico da Guia) is an aerial gondola lift system at Guia Hill, Macau. The system connects Jardim da Flora with Parque Municipal da Colina da Guia. It opened in 1997 and has nine cars (each holding four passengers). Visitors can gain a bird's-eye view of the garden and a panoramic perspective of the city.[1] The ride takes 80 seconds.[2] Ticket price...
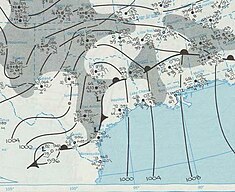
1971 tornado across the Mississippi Delta 1971 Inverness tornado Aerial of Inverness, MS after the tornado.Meteorological historyFormedFeb 21, 1971, 3:08 p.m. CDT (UTC−05:00)DissipatedFeb 21, 1971, 5:10 pm. CDT (UTC−05:00)Duration1 hour, 25 minutes F5 tornadoon the Fujita scaleOverall effectsFatalities48Injuries510Part of the Tornado outbreak of February 21–22, 1971 On the afternoon of Sunday, February 21, 1971, a deadly and long-tracked F5 tornado impacted the Mississippi Del...

Japanese manga series Strawberry MarshmallowVolume 1 of the English version of the manga.苺ましまろ(Ichigo Mashimaro)GenreComedy, slice of life[1] MangaWritten byBarasuiPublished byASCII Media WorksEnglish publisherAUS: Madman (formerly)NA: Tokyopop (formerly)UK: Tokyopop (formerly)MagazineDengeki DaiohDemographicShōnenOriginal runFebruary 15, 2002 – presentVolumes9 Anime television seriesDirected byTakuya SatōWritten byTakuya SatōMusic byTakeshi Wat...

German agricultural scientist and politician Andreas HermesHermes in the late 1940sReich Minister of FinanceIn office26 October 1921 – 13 August 1923ChancellorJoseph WirthWilhelm CunoPreceded byJoseph WirthSucceeded byRudolf HilferdingReich Minister for Food and AgricultureIn office30 March 1920 – 30 March 1922ChancellorHermann MüllerConstantin FehrenbachJoseph WirthPreceded byKarl MüllerSucceeded byGerhard von KanitzMember of the ReichstagIn office14 June 1928 �...

United Nations resolution adopted in 1995 UN Security CouncilResolution 985A Nigerian ECOMOG soldier in LiberiaDate13 April 1995Meeting no.3,517CodeS/RES/985 (Document)SubjectLiberiaVoting summary15 voted forNone voted againstNone abstainedResultAdoptedSecurity Council compositionPermanent members China France Russia United Kingdom United StatesNon-permanent members Argentina Botswana Czech Republic Germany Honduras Indonesia I...

Oscar CamenzindOscar Camenzind alla Parigi-Nizza 1997Nazionalità Svizzera Altezza173[1] cm Peso61[1] kg Ciclismo SpecialitàStrada Termine carriera2004 CarrieraSquadre di club 1996 Panaria1997-1998 Mapei1999-2001 Lampre2002-2004 Phonak Nazionale 1996-2003 Svizzera Palmarès Mondiali OroValkenburg 1998In linea Modifica dati su Wikidata · Manuale Oscar Camenzind (Svitto, 12 settembre 1971) è un ex ciclista su strada svizzero. Profess...

Questa voce o sezione sull'argomento calcio a 5 non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Taça de Portugal de FutsalSport Calcio a 5 TipoClub FederazioneUEFA OrganizzatoreFederazione calcistica del Portogallo Cadenzaannuale Aperturaautunno Partecipanti110 StoriaFondazione1997 DetentoreBenfica Recor...


![{\displaystyle \forall i\in [\![1,j]\!],\forall k\in [\![0,m_{i-1}]\!],P^{(k)}(\lambda _{i})=f^{(k)}(\lambda _{i})=Q^{(k)}(\lambda _{i}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6f644d721714198e782fe25eadace70c6620c60)



















![{\displaystyle \ln :\mathrm {M} _{n}(\mathbb {C} )\to \mathrm {M} _{n}(\mathbb {C} ),\quad A\mapsto \mathrm {\ln(} A)=-2\sum _{k\in \mathbb {N} }{\frac {1}{2k+1}}\left[(\mathrm {I} _{n}-A)(\mathrm {I} _{n}+A)^{-1}\right]^{2k+1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01d3a70cc4c4f8a27ff9cbb3434aca8fe356954e)
![{\displaystyle P=\sum _{k=0}^{d}a_{k}X^{k}\in \mathbb {K} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81ee0e89fd14a97672ff3ded2b14c8716f2105ad)

![{\displaystyle f(A)={\frac {1}{2}}\left(f(\lambda _{+})+f(\lambda _{-})-{\frac {\mathrm {Tr} (A)}{\sqrt {\mathrm {Tr} (A)^{2}-4\,\mathrm {det} (A)}}}\left[f(\lambda _{+})-f(\lambda _{-})\right]\right)\mathrm {I} _{2}+{\frac {\left[f(\lambda _{+})-f(\lambda _{-})\right]}{\sqrt {\mathrm {Tr} (A)^{2}-4\,\mathrm {det} (A)}}}A~,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acd5f5068fed8c9f4914ab5a05b0f24bbfc63db0)




