Arbre bouc-émissaire
|
Read other articles:

Katedral RagusaKatedral Santo Yohanes PembaptisItalia: Cattedrale di S. Giovanni Battistacode: it is deprecated Katedral RagusaLokasiRagusa, SisiliaNegaraItaliaDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupanKeuskupan Ragusa Katedral Ragusa (Italia: Duomo di Ragusa, Cattedrale di San Giovanni Battistacode: it is deprecated ) adalah sebuah gereja katedral Katolik yang terletak di Ragusa, Sisilia, Italia. Katedral ini didedikasikan untuk Santo Yoh...
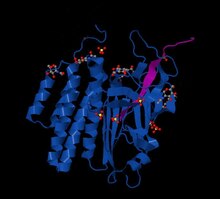
Famili GPCR adhesi manusia. Anggota didefinisikan oleh struktur hibrida yang tidak biasa dengan wilayah ekstraseluler yang panjang sering mengandung protein modul yang dikenal digabungkan ke daerah transmembran tujuh rentang melalui domain GPCR-Autoproteolsis INducing (GAIN) GPCR adhesi (adhesion G protein-protein-coupled receptor) adalah kelas 33 reseptor protein manusia dengan distribusi yang luas di sel embrio dan larva, sel-sel dari saluran reproduksi, neuron, leukosit, dan berbagai tumor...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Mahmoud al-Zahar – berita · surat kabar · buku · cendekiawan · JSTOR Mahmoud al-Zahar300x300px Nama dalam bahasa asli(ar) م BiografiKelahiran6 Mei 1945 (78 tahun)Gaza Kementerian Luar Negeri dan Ekspatr...

The Colombo Express, salah satu kapal peti kemas yang terbesar yang dioperasikan oleh Hapag-Lloyd dari Jerman Kapal peti kemas (Inggris: containership atau celullarship) adalah kapal yang khusus digunakan untuk mengangkut peti kemas yang standar. Memiliki rongga (cells) untuk menyimpan peti kemas ukuran standar. Peti kemas diangkat ke atas kapal di terminal peti kemas dengan menggunakan kran/derek khusus yang dapat dilakukan dengan cepat, baik derek-derek yang berada di dermaga, maupun derek ...

Persatuan Sepak Bola Afrika BaratUnion des Fédérations Ouest-Africaines de Football Zona A Zona BTanggal pendirian1975; 49 tahun lalu (1975)TipeOrganisasi OlahragaWilayah layanan Afrika BaratJumlah anggota Zona A – 9 anggota Gambia Guinea Guinea-Bissau Liberia Mali Mauritania Senegal Sierra Leone Tanjung Verde Zona B – 7 anggota Benin Burkina Faso Ghana Niger Nigeria Pantai Gading Togo Bahasa resmi Inggris, Prancis dan PortugisAfiliasiCAF, ...

René Teulade Fonctions Sénateur français 1er octobre 2008 – 13 février 2014(5 ans, 4 mois et 12 jours) Élection 21 septembre 2021 Circonscription Corrèze Groupe politique SOC Prédécesseur Bernard MuratGeorges Mouly Successeur Patricia Bordas 1er vice-président du Conseilgénéral de la Corrèze 20 mars 2008 – 31 mars 2011 (3 ans et 11 jours) Président François Hollande Prédécesseur Georges Mouly Successeur Gérard Bonnet Conseiller général de la Co...

Oriental ClubStratford HouseFormation1824(Clubhouse occupied since 1962)PurposeEast India Company civil and military officers who served in the EastHeadquartersStratford HouseLocationLondon, WC1 The Oriental Club in London is an exclusive Private Members’ Club established in 1824.[1] Charles Graves describes it as fine in quality as White's but with the space of infinitely larger clubs.[2] It is located in Stratford Place, near Oxford Street and Bond Street. Foundation The ...

Disambiguazione – Se stai cercando l'omonimo comune del Kentucky, vedi Edmonton (Kentucky). Edmontoncittà (city)City of Edmonton Edmonton – Veduta LocalizzazioneStato Canada Provincia Alberta Divisione censuariaDivisione No. 11 AmministrazioneSindacoAmarjeet Sohi (Partito Liberale del Canada) dal 29-10-2021 TerritorioCoordinate53°32′N 113°30′W / 53.533333°N 113.5°W53.533333; -113.5 (Edmonton)Coordinate: 53°32′N 113°30′W / &#x...

Vadenacomune(IT) Vadena(DE) Pfatten Vadena – Veduta LocalizzazioneStato Italia Regione Trentino-Alto Adige Provincia Bolzano AmministrazioneSindacoElmar Oberhofer (SVP) dal 22-9-2020 Lingue ufficialiItaliano, Tedesco TerritorioCoordinate46°24′50.38″N 11°18′18.28″E / 46.413995°N 11.305077°E46.413995; 11.305077 (Vadena)Coordinate: 46°24′50.38″N 11°18′18.28″E / 46.413995°N 11.305077°E46.413995; 11.305077 (Va...

American heavy metal supergroup For other uses, see Hell Yeah (disambiguation). HellyeahHellyeah performing in 2013Background informationOriginDallas, Texas, U.S.Genres Groove metal heavy metal alternative metal Years active2006–2021 (indefinite hiatus)Labels Eleven Seven Epic Past members Chad Gray Christian Brady Tom Maxwell Kyle Sanders Roy Mayorga Vinnie Paul Greg Tribbett Bob Zilla Jerry Montano Websitehellyeahband.com Hellyeah, stylized as HELLYEAH, was an American heavy metal supergr...

Canadian mixed martial artist Gillian RobertsonRobertson in 2024Born (1995-05-17) May 17, 1995 (age 28)Niagara Falls, Ontario, Canada[1]Other namesThe SavageHeight5 ft 5 in (1.65 m)Weight115 lb (52 kg; 8 st 3 lb)DivisionStrawweight (2016, 2023–) Flyweight (2016–2022)Reach63[1] in (160 cm)StyleBrazilian Jiu-Jitsu, KickboxingFighting out ofPort Saint Lucie, Florida, United States[2]TeamAmerican Top Team (2011–2020)&...

2011 single by Nicki Minaj featuring Rihanna FlySingle by Nicki Minaj featuring Rihannafrom the album Pink Friday ReleasedAugust 30, 2011Recorded2010StudioGlenwood Place Studios (Burbank, California); Chalice Recording Studios (Los Angeles, California)Length3:32Label Young Money Cash Money Universal Motown Universal Republic Songwriter(s) Kevin Hissink W. Jordan Onika Maraj J.R. Rotem Clemm Rishad Producer(s) J.R. Rotem Skrt Kevin Hissink Nicki Minaj singles chronology Lollipop Luxury (20...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...
Short story by Hans Christian AndersenThe AngelShort story by Hans Christian AndersenIllustration from the 1888 anthology Hans Andersen's Fairy TalesOriginal titleEnglenCountryDenmarkLanguageDanishGenre(s)Literary fairy talePublicationPublished inNew Fairy Tales. First Volume. First Collection (Nye Eventyr. Første Bind. Første Samling)Publication typeFairy tale collectionPublisherC.A. ReitzelMedia typePrintPublication date11 November 1843Chronology — The Nighting...

La consommation de carburant d’une automobile est le volume de carburant utilisé lors d'un trajet rapporté à la distance parcourue. L’unité utilisée pour la consommation de carburant est le « litre pour cent kilomètres » (noté l/100 km)[1]. En Europe, la consommation de carburant fait partie des données nécessaires pour l'homologation des véhicules automobiles. La réduction de consommation des véhicules automobiles constitue un enjeu important pour la société par...

دير الزور دير الزور اللقب لؤلؤة الفرات تاريخ التأسيس 1865 ميلادي تقسيم إداري البلد سوريا[1] عاصمة لـ محافظة دير الزورمتصرفية الزور المحافظة محافظة دير الزور خصائص جغرافية إحداثيات 35°20′00″N 40°09′00″E / 35.333333°N 40.15°E / 35.333333; 40.15 الارتفاع 253 متر (830 قدم) ...

33°40′N 47°00′E / 33.667°N 47.000°E / 33.667; 47.000 زاغروس سلسلة جبال زاغروس الموقع إيران العراق إحداثيات 33°40′00″N 47°00′00″E / 33.666667°N 47°E / 33.666667; 47 الارتفاع 4409 متر الطول 1500 كيلومتر المساحة 533512 كيلومتر مربع القمة الأم زرد كوه [لغات أخرى] تع...
American superhero television series Gen VAlso known asThe Boys: Gen VGenre Black comedy Drama Superhero Based onThe Boys Volume 4: We Gotta Go Nowby Garth EnnisDarick RobertsonDeveloped by Craig Rosenberg Evan Goldberg Eric Kripke Showrunners Michele Fazekas Tara Butters Starring Jaz Sinclair Chance Perdomo Lizze Broadway Maddie Phillips London Thor Derek Luh Asa Germann Shelley Conn Composers Matt Bowen Christopher Lennertz Country of originUnited StatesOriginal languageEnglishNo. of season...

This template does not require a rating on Wikipedia's content assessment scale.It is of interest to the following WikiProjects:Stub sorting This template is maintained by WikiProject Stub sorting, an attempt to bring some sort of order to Wikipedia. If you would like to participate, you can choose to improve/expand the articles containing this stub notice, or visit the project page, where you can join the project and see a list of open tasks.Stub sortingWikipedia:WikiProject Stub sortingTemp...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Elektronika digital – berita · surat kabar · buku · cendekiawan · JSTOR Hitachi J100 dapat disesuaikan dan sasis penggerak frekuensi dunia AS Elektronika digital adalah sistem elektronika yang menggunaka...
























































