Ajustement dynamique de la tension

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus.
Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus.

Cet article ne cite pas suffisamment ses sources ().

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

Cet article est une ébauche concernant l’informatique, l’électronique et l’électricité.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

L'ajustement dynamique de la tension des processeurs (en anglais dynamic voltage scaling) est une technique de gestion de la tension électrique utilisée dans les architectures des ordinateurs.

Cette technique consiste à augmenter ou réduire la tension des courants électriques qui parcourent le processeur. L'augmentation de la tension est généralement utilisée pour augmenter la fiabilité d'un système, la réduction permet, quant à elle, de réduire la consommation d'énergie.

Cette technique est utilisée massivement dans les appareils mobiles tels quel les téléphones mobiles, les tablettes et les ordinateurs portables.

L'ajustement dynamique de la tension est à ne pas confondre avec l'ajustement dynamique de la fréquence (Dynamic frequency scaling) d'un processeur.

Notes et références

v · m
Technologies de processeur
Modèles
Architecture
Général
Mots
Instruction
Jeu
Famille
Exécution
Performance
Types
Général
Par usage
On chip
Accélération
matérielle
Microarchitecture
Parallélisme
Général
Processus
Taxonomie de Flynn
Circuiterie et unité
Général
Exécution
Porte logique
Registre
Contrôle
Chemin de données
Cadencement
Gestion de l'alimentation
Fabrication
Articles liés

Read other articles:

2023 Zimbabwean general election

2023 Zimbabwean general election ← 2018 23 August 2023 (2023-08-23) 2028 → ← outgoing memberselected members → Presidential electionRegistered6,623,511 ( 16.29%)Turnout68.86% ( 16.24pp)   Candidate Emmerson Mnangagwa Nelson Chamisa Party ZANU–PF CCC Popular vote 2,350,711 1,967,343 Percentage 52.60% 44.03% President before election Emmerson Mnangagwa ZANU–PF Elected President Emmerson Mnangagwa ZANU–PF National Assemb...

 

puasa

Halaman ini berisi artikel tentang tindakan berpuasa dalam cakupan umum. Untuk tindakan berpuasa khusus dalam Islam, lihat Saum. Anak kecil lagi menunggu waktu puasa Puasa atau saum secara bahasa adalah meniadakan makan, minum, dan sebagainya dengan sengaja.[1][2] Puasa mutlak biasanya didefinisikan menahan diri dari hal-hal yang membatalkan puasa dengan tujuan taat Kepada Allah SWT dengan niat khusus. Puasa lain, membatasi makanan tertentu atau zat. Praktik puasa dapat mengha...

 

Cincinnati, Ohio

Cincinnati beralih ke halaman ini. Untuk kegunaan lain, lihat Cincinnati (disambiguasi). Cincinnati, OhioKotaKota CincinnatiDowntown Cincinnati from Devou Park in Covington, Kentucky BenderaLambangJulukan: The Queen City, Cincy, The Fountain CityMotto: Juncta Juvant (Lat. Strength in Unity)Location in Hamilton County and the state of Ohio.NegaraAmerika SerikatNegara BagianOhioWilayahHamiltonTerbentuk1788Bermukim1802 sebagai Desa / 1819 Sebagai KotaPemerintahan • JenisWal...

Zaqatala (rayon)

Zaqatala Kota: Zaqatala Ketinggian: 500m Populasi: 35.000 Map of Azerbaijan showing Zaqatala rayon Zaqatala adalah rayon di Azerbaijan. Ibu kota dan kota penting rayon ini adalah Zaqatala. Zaqatala terkenal untuk Hazelnut dan Walnutnya. Ekonomi rayon ini bergantung pada sektor agrikultur. lbsPembagian administratif Azerbaijan Distrik Absheron Agdam Agdash Aghjabadi Agstafa Agsu Astara Babek Balakan Barda Beylagan Bilasuvar Dashkasan Fuzuli Gadabay Goranboy Goychay Goygol Hajigabul Imishli Is...

 

Nassau, Bahama

Nassau City of NassauMotto: Forward, Upward, Onward, Together (Maju, Ke Atas, Ke Depan, Bersama)Negara BahamapulauNew ProvidenceDidirikan1695Luas • Total207 km2 (80 sq mi)Populasi (2010) • Total248.948 • Kepadatan1,200/km2 (3,100/sq mi) • Kepadatan metropolitan1.203/km2 (3,120/sq mi)Zona waktuUTC−5 (EST) • Musim panas (DST)UTC−4 (EDT)Kode area telepon242 Nassau /ˈnæsɔː/ adalah ibu ...

 

UFC Fight Night: Lee vs. Oliveira

UFC mixed marial arts event in 2020 UFC Fight Night: Lee vs. OliveiraThe poster for UFC Fight Night: Lee vs. OliveiraInformationPromotionUltimate Fighting ChampionshipDateMarch 14, 2020 (2020-03-14)VenueGinásio Nilson NelsonCityBrasília, BrazilAttendanceNone (behind closed doors)[1]Event chronology UFC 248: Adesanya vs. Romero UFC Fight Night: Lee vs. Oliveira UFC Fight Night: Woodley vs. Edwards UFC Fight Night: Lee vs. Oliveira (also known as UFC Fight Night 170 and...

GSAT-8

GSAT-8GSAT-8Mission typeCommunicationOperatorINSATCOSPAR ID2011-022A SATCAT no.37605Mission durationPlanned: 12 years Elapsed: 12 years, 11 months, 6 days Spacecraft propertiesBusI-3KManufacturerISROLaunch mass3,093 kilograms (6,819 lb)[1]Dry mass1,426 kilograms (3,144 lb)[1]Power6,242 watts[1] Start of missionLaunch date20 May 2011, 20:38 (2011-05-20UTC20:38Z) UTCRocketAriane 5ECA VA202Launch siteKourou ELA-3ContractorArianespac...

 

Margery Kempe

English mystic (c. 1373 – after 1438) Margery KempeBornMargery Brunhamc. 1373Bishop's Lynn, EnglandDiedAfter 1438OccupationChristian mysticLanguageEnglishNotable worksThe Book of Margery Kempe Margery Kempe (c. 1373 – after 1438) was an English Christian mystic, known for writing through dictation The Book of Margery Kempe, a work considered by some to be the first autobiography in the English language. Her book chronicles her domestic tribulations, her extensive pilgrimages t...

 

South Keys Shopping Centre

Strip mall in Ottawa, Ontario South Keys Shopping CentreAddress2210 Bank StreetOttawa, ONK1V 1J5Opening date1996OwnerSmartCentresNo. of stores and services20No. of anchor tenants1Total retail floor area486,127 sq ft (45,162.7 m2)Parking2,982Public transit access Greenboro South KeysWebsiteSmartCentres Ottawa South South Keys Shopping Centre, officially SmartCentres Ottawa South, is a shopping centre in the South Keys neighbourhood of Ottawa, Ontario, Canada. It is owned and ope...

西遊記大結局之仙履奇緣

本條目存在以下問題，請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修，以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引，幫助编辑這個條目。（幫助、討論） 此條目剧情、虛構用語或人物介紹过长过细，需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸，輔助�...

 

All fourths tuning

Guitar Tuning All fourthsThe consecutive open notes of all-fourths tuning are spaced apart by five semitones on the chromatic circle, which lists the twelve notes of the octave.Basic informationAliasesPerfect-fourths tuningIntervalPerfect fourthSemitones5Example(s)E-A-D-G-C-FAdvanced informationOther instrumentsBass guitarRepetitionNoAdvantagesClosely approximates standard tuningDisadvantagesDifficult to play conventional music, especially barre chordsLeft-handed tuningAll-fifths tu...

 

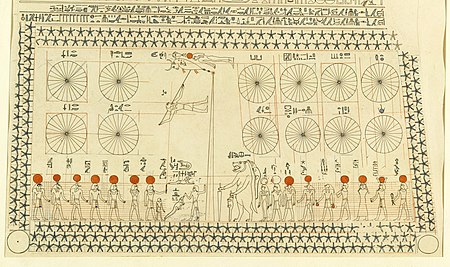
تصنيف:شهور التقويم المصري

عنتشهور التقويم المصري توت بابة هاتور كيهك طوبة أمشير برمهات برمودة بشنس بؤونة أبيب مسرى نسيئ تصنيف:شهور التقويم المصري

Frederic Edwin Church

American landscape painter (1826–1900) Frederic Edwin Churchc. 1868 photograph by Napoleon SaronyBorn(1826-05-04)May 4, 1826Hartford, Connecticut, U.S.DiedApril 7, 1900(1900-04-07) (aged 73)New York City, U.S.Known forLandscape paintingNotable workNiagara, The Heart of the AndesMovementHudson River School Frederic Edwin Church (May 4, 1826 – April 7, 1900) was an American landscape painter born in Hartford, Connecticut. He was a central figure in the Hudson River School of...

 

Papakating Creek

Creek in Sussex County, New Jersey, U.S. Papakating CreekPepper-Cotton, Pellettown Creek, Pellet CreekLooking south from County Route 565 in Wantage TownshipEtymologyMunsee (northern Lenape dialect)LocationCountryUnited StatesStateNew JerseyCountySussexMunicipalityFrankford Township, Wantage TownshipPhysical characteristicsSourceFrankford Township, at foot of Kittatinny Mountain • coordinates41°12′36″N 74°43′02″W / 41.21000°N 74.71722°W...

 

Caduta (astrologia)

Questa voce sull'argomento astrologia è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. I segni ed il grado massimo di caduta per i diversi pianeti indicato in rosso, complementare a quello di esaltazione (in verde) del segno opposto In astrologia, la caduta di un pianeta o luminare si determina quando esso si trova in opposizione al segno zodiacale in cui ha la sua esaltazione. Un pianeta in caduta si t...

Cootes Paradise

Property of the Royal Botanical Gardens at the western end of Lake Ontario See also: Geography of Hamilton, Ontario Cootes Paradise is a property with many boundaries, but is primarily a property of the Royal Botanical Gardens at the western end of Lake Ontario, but is also remnant of the larger 3700 acre Dundas Marsh Crown Game Preserve established by the province of Ontario in 1927.,[1] dominated by a 4.5 km long rivermouth wetland, representing the lake's western terminus. It ...

 

McLaren M28

McLaren M28La McLaren M28C al Museo di Donington ParkDescrizione generaleCostruttore  McLaren CategoriaFormula 1 SquadraMarlboro Team McLaren Progettata daGordon Coppuck SostituisceMcLaren M26 Sostituita daMcLaren M29 Descrizione tecnicaMeccanicaTelaiomonoscocca d'alluminio MotoreFord Cosworth DFV da 485 CV a 10.600 giri/min TrasmissioneHewland FGA 400/6, manuale a 6 rapporti. Dimensioni e pesiLunghezza4420 mm Larghezza2134 mm Altezza1016 mm Passo2870 mm Peso675 kg AltroPneumaticiGoodyea...

 

Väinö Tiiri

Questa voce sull'argomento ginnasti finlandesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Väinö TiiriNazionalità Finlandia Ginnastica artistica Palmarès Competizione Ori Argenti Bronzi Giochi olimpici 0 1 1 Vedi maggiori dettagliIl simbolo → indica un trasferimento in prestito.   Modifica dati su Wikidata · Manuale Väinö Edward Tiiri (Loimaa, 31 gennaio 1886 – Helsinki, 30 luglio 1966) è stato un ginnasta finlandese. In...

Brasserie

Pour l’article homonyme, voir Brasserie (restaurant). Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (février 2013). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». ...

 

Molares Volumen

Physikalische Größe Name Molares Volumen Formelzeichen V m {\displaystyle V_{\mathrm {m} }} Größen- undEinheitensystem Einheit Dimension SI m3·mol−1 L3 N−1 Das molare Volumen oder auch Molvolumen (Formelzeichen: Vm) eines Stoffes gibt an, welches Volumen ein Mol dieser Substanz einnimmt. Seine SI-Einheit ist m3/mol. Es ergibt sich aus dem Quotienten des Volumens V und der Stoffmenge n und kann aus der Molaren Masse M und der Dichte ρ der entsprechenden Substanz berechnet werden. V ...