2-opt
|
Read other articles:

Ganga JamunaPoster PromosionalSutradaraManmohan DesaiProduserS. RamanathanDitulis olehKader Khan, Sohel Don, Anil NagrathSkenarioK.K. ShuklaCeritaPrayag RajPemeranAmitabh BachchanMithun ChakrabortyMeenakshi SheshadriJaya PradaNirupa RoyAmrish PuriPenata musikAnu MalikSinematograferPravin BhattTanggal rilis 29 Desember 1988 (1988-12-29) Durasi187 menitBahasaHindiAnggaranRs 10 crores Ganga Jamuna Saraswati adalah film Hindi 1988 yang disutradarai oleh Manmohan Desai, dibiayai oleh Ha...

RatatouillePoster ASSutradaraBrad BirdJan PinkavaProduserBrad LewisDitulis olehBrad BirdCeritaJan PinkavaJim CapobiancoBrad BirdEmily CookKathy GreenbergPemeranPatton OswaltLou RomanoPeter SohnBrad GarrettJaneane GarofaloIan HolmBrian DennehyPenata musikMichael GiacchinoPenyuntingDarren T. HolmesDistributorWalt Disney PicturesTanggal rilisDurasi111 menitBahasaInggrisAnggaranUS$150 juta[1]IMDbInformasi di IMDbAMGProfil All Movie Guide Ratatouille (IPA: /ˌɹætəˈtui, -ˈtwi/; b...

العلاقات الأوكرانية البرتغالية أوكرانيا البرتغال أوكرانيا البرتغال تعديل مصدري - تعديل العلاقات الأوكرانية البرتغالية هي العلاقات الثنائية التي تجمع بين أوكرانيا والبرتغال.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدو�...

Highland Scottish clan Lord Maclean redirects here. For the 1990–2005 Senator of the College of Justice (judge), see Ranald MacLean, Lord MacLean. Clan MacleanClann 'IllEathain, Clann MhicIllEathain, Na Leathanaich[1]Crest: A tower embattled ArgentMottoVirtue Mine Honour (My Virtues are my Honour)SloganBàs no Beatha (Death or victory)ProfileRegionHighlandsDistrictInner HebridesPlant badgecrowberry or hollyChiefLachlan Hector Charles Maclean of Duart and MorvenThe 12th Baronet of Mo...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Agriculture in Bahrain – news · newspapers · books · scholar · JSTOR (April 2009) This article ne...

Erhard MaertensErhard Maertens, before May 1945Other name(s)Eberhard MaertensBorn(1891-02-26)26 February 1891GłogówDied5 May 1945(1945-05-05) (aged 54)BerlinAllegianceGermanyService/branchKriegsmarineRankVizeadmiralCommands heldNaval Academy MürwikBattles/warsWorld War II Erhard Maertens or Eberhard Maertens (26 February 1891 – 5 May 1945)[1][2] was a German Vizeadmiral of the Kriegsmarine during World War II. From 16 June 1941 to 5 May 1943, he was Chief of Office ...

此條目可参照英語維基百科相應條目来扩充。 (2021年10月13日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 国际调查记者同盟International Consortium of Investigative Journalists成立時間1997年總部华盛顿哥伦比亚特区 地址�...

Public university in Hefei, Anhui, China Not to be confused with Hebei University of Technology. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hefei University of Technology – n...

Flag of a Space Forcelieutenant general This is a complete list of lieutenant generals in the United States Space Force. The rank of lieutenant general (or three-star general) is the second-highest rank achievable in the U.S. Space Force, and the first to have a specific number of authorized positions for it set by statute. It ranks above major general (two-star general) and below general (four-star general). There have been 11 lieutenant generals in the United States Space Force, three of w...

オリンピックカラーのライトアップで照らされた東京都庁 TOKYOの文字が表示された東京タワー 東京オリンピック誘致のラッピング装飾が施された都営バス(2008年6月撮影) この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 2016年東京オリンピ�...

زيروكسالشعارمعلومات عامةسميت باسم تصوير جاف البلد الولايات المتحدة[1] التأسيس 18 أبريل 1906 النوع عمل تجاري — مقاولة — شركة عمومية محدودة الشكل القانوني شركة مساهمة — شركة عمومية محدودة المقر الرئيسي نوروولك على الخريطة — كونيتيكت — روتشستر — نيويورك الجوائز ا�...

Family of low-floor trams and light rail vehicles A Citadis 302 in Mulhouse Citadis Spirit, the model designed for Canadian operators, seen on Ottawa's Confederation Line The Alstom Citadis is a family of low-floor trams and light rail vehicles built by Alstom. As of 2017[update], over 2,300 Citadis trams have been sold and 1,800 tramways are in revenue service throughout the world, with operations in all six inhabited continents.[1] An evolution of Alstom's earlier TFS vehicl...

Basilica dei Santi Giovanni e PaoloEsternoStato Italia RegioneVeneto LocalitàVenezia Coordinate45°26′21.48″N 12°20′31.92″E45°26′21.48″N, 12°20′31.92″E ReligioneCattolica romana TitolareGiovanni e Paolo OrdineDomenicano Patriarcato Venezia Consacrazione1430 Stile architettonicogotico Completamento1343 Demolizione1810 Sito webSito ufficiale Modifica dati su Wikidata · Manuale La basilica dei Santi Giovanni e Paolo (San Zanìpoło in veneziano) è uno degli edific...

LHDLarge Helical DeviceThe Large Helical Device in 2014Device typeHeliotronLocationToki, JapanAffiliationNational Institute for Fusion ScienceTechnical specificationsMajor radius3.9 m (13 ft)Minor radius0.6 m (2 ft 0 in)Magnetic field3.0 T (30,000 G)HistoryYear(s) of operation1998–present The Large Helical Device (大型ヘリカル装置, Ōgata Herikaru Sōchi) (LHD) is a fusion research device located in Toki, Gifu, Japan. It is operated by the National...

American military machine gun deployed 1957 For other uses, see M60 (disambiguation). Machine Gun, Caliber 7.62 mm, M60 M60 machine gun with bipod foldedTypeGeneral-purpose machine gun Medium machine gunPlace of originUnited StatesService historyIn service1957–presentUsed bySee UsersWars Vietnam War Laotian Civil War Dominican Civil War[1] Cambodian Civil War Moro conflict The Troubles Lebanese Civil War Cambodian–Vietnamese War Sino-Vietnamese War[2&#...

Mosque in Washington, D.C. Islamic Center of WashingtonReligionAffiliationIslamLocationLocationWashington, United StatesShown within the United StatesGeographic coordinates38°55′1.6″N 77°3′24.3″W / 38.917111°N 77.056750°W / 38.917111; -77.056750ArchitectureTypeMosqueCompleted1954SpecificationsMinaret(s)1Minaret height160 feet (49 m)[1]Websitewww.theislamiccenter.com The Islamic Center of Washington is a mosque and Islamic cultural center in Was...
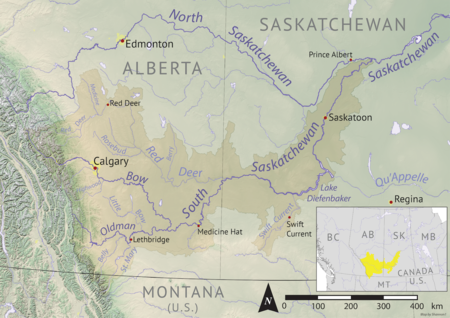
River in Western Canada South Saskatchewan RiverThe University Bridge over the South Saskatchewan River at SaskatoonThe South Saskatchewan River drainage basinThe mouth in SaskatchewanShow map of SaskatchewanSouth Saskatchewan River (Canada)Show map of CanadaLocationCountryCanadaProvincesAlbertaSaskatchewanPhysical characteristicsSource confluenceOldman and Bow Rivers • locationMunicipal District of Taber, Alberta • coordinates49°56′00″N 111°41′30�...

Modern writing system for the Vietnamese language This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Vietnamese alphabet – news · newspapers · books · scholar · JSTOR (April 2018) (Learn how and when to remove this message) Vietnamese alphabetchữ Quốc ngữScript type Alphabet CreatorPortuguese and Italian ...

Senior Second Rank ViscountYoshitami Matsudaira松平慶民Born(1882-03-13)March 13, 1882DiedJuly 18, 1948(1948-07-18) (aged 66)Alma materBalliol College, OxfordFatherMatsudaira YoshinagaFamilyYoshichika Tokugawa (brother) Viscount Yoshitami Matsudaira was a Japanese bureaucrat. He served as the last Grand Steward of the Imperial Household Office (now the Imperial Household Agency) (1947–1948). He spent 12 years of his youth in England and was educated at Balliol College, Oxford.&...

Mausoleum Jenghis Khan Hanzi: 成吉思汗陵 Alih aksara Mandarin - Hanyu Pinyin: Chéngjísī Hán líng - Wade-Giles: Ch‘êng-chi-ssu Han Ling Mausoleum Genghis Khan adalah sebuah mausoleum yang ditujukan untuk menghormati Genghis Khan yang terletak di Prefektur Ordos, Mongolia Dalam, Tiongkok. Tempat tersebut berisi sejumlah barang pribadinya. Tempat tersebut mendapatkan predikat obyek wisata tingkat nasional 5A. Selain itu, sejumlah upacara juga dilaksanakan di tempat tersebut, sepert...














