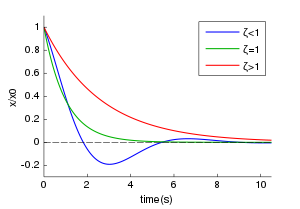
Harmoninen värähtelijä
|
Read other articles:

Glenea citrina Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Subfamili: Lamiinae Tribus: Saperdini Genus: Glenea Spesies: Glenea citrina Glenea citrina adalah spesies kumbang tanduk panjang yang tergolong famili Cerambycidae. Spesies ini juga merupakan bagian dari genus Glenea, ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan ...

Freno a tamburo di un'auto Il freno a tamburo è costituito da un cilindro rotante (detto tamburo) solidale col sistema da frenare e da uno o più ceppi realizzati in materiale d'attrito atti ad esercitare una forza sul cilindro e che prendono il nome di ganasce. Il ceppo può essere sia interno che esterno al rullo. Un esempio del tipo interno è quello delle automobili, un esempio del tipo esterno è quello dei carri. Indice 1 Storia 2 Comando e azionamento dei freni 3 Tamburo e piatto 4 Ce...

1971 novel by Beatrice Sparks This article is about the book. For the song by Jefferson Airplane, see White Rabbit (song). Go Ask Alice Dust jacket of Prentice Hall first edition, 1971AuthorBeatrice SparksLanguageEnglishGenreYoung adult fictionPublished1971Publisher Prentice Hall (1st edition) Simon & Schuster (later editions) Media typePrint (hardcover and paperback), ebookISBN0-671-66458-1OCLC164716LC ClassPZ7 .G534 Go Ask Alice is a 1971 book about a teenage girl who develops...

العلاقات البوليفية المصرية بوليفيا مصر بوليفيا مصر تعديل مصدري - تعديل العلاقات البوليفية المصرية هي العلاقات الثنائية التي تجمع بين بوليفيا ومصر.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة بوليفيا مص...

Gopalkrishna Gandhi Gubernur Bengal Barat ke-23Masa jabatan14 Desember 2004 – 14 Desember 2009PendahuluViren J. ShahPenggantiDevanand KonwarGubernur Bihar ke-21Masa jabatan31 Januari 2006 – 21 Juni 2006PendahuluButa SinghPenggantiR. S. Gavai Informasi pribadiLahirGopalkrishna Devdas Gandhi22 April 1945 (umur 79)Delhi, India BritaniaPartai politikIndependenAfiliasi politiklainnyaAliansi Progresif BersatuSuami/istriTara GandhiAnak2 putriOrang tuaDevdas GandhiLakshmi G...

Basilika Tempat Ziarah Nasional Bunda Maria dari Aparecida di Aparecida, Brazil adalah gereja terbesar kedua di dunia setelah Basilika Santo Petrus di Kota Vatikan. Bagian dari seriGereja Katolik menurut negara Afrika Afrika Selatan Afrika Tengah Aljazair Angola Benin Botswana Burkina Faso Burundi Chad Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Guinea Khatulistiwa Jibuti Kamerun Kenya Komoro Lesotho Liberia Libya Madagaskar Malawi Mali Maroko Mauritania Mauritius Mesir M...

Public radio network in Montana, US Yellowstone Public RadioTypePublic Radio NetworkCountryUnited StatesBroadcast areaMontanaIdahoWyomingProgrammingAffiliationsNational Public RadioOwnershipOwnerMontana State University-BillingsLinksWebcastAvailable on websiteWebsiteyellowstonepublicradio.org Yellowstone Public Radio is a public radio regional network based in Billings, Montana with transmitters covering most of Montana, as well as northern Wyoming and eastern Idaho. It is operated by Montana...

نهائي الدرع الخيرية 1964الحدثنهائي الدرع الخيرية 1964 وست هام يونايتد ليفربول 2 2 التاريخ15 أغسطس 1964الملعبملعب أنفيلد، ليفربولالحكمكين ستوكسالحضور36,493 → 1963 1965 ← نهائي الدرع الخيرية 1964 هي النسخة 42 من الدرع الخيرية. لعبت المباراة بتاريخ 15 أغسطس 1964 على ملعب أنفيلد، بين وست هام يو�...

This article is about the troubadour. For his grandfather, see Raimbaut, Count of Orange. 12th-century Occitan nobleman Raimbaut depicted in a 13th-century chansonnier Raimbaut of Orange (Old Provençal: Raimbaut d'Aurenga; c. 1147 – 1173) was the lord of Orange and Aumelas and an influential troubadour in medieval France. His properties included the towns of Frontignan and Mireval. He was the only son of William of Aumelas and of Tiburge, Countess of Orange, daughter of Raimbaut, Count...

County in New York, United States For the town of Columbia, see Columbia, New York. County in New YorkColumbia CountyCountyFirst Columbia County Courthouse in Claverack FlagSealLocation within the U.S. state of New YorkNew York's location within the U.S.Coordinates: 42°15′N 73°38′W / 42.25°N 73.63°W / 42.25; -73.63Country United StatesState New YorkFoundedApril 4, 1786; 238 years ago (1786-04-04)[nb 1]Named forChristopher Col...

Form of government and succession of power Part of the Politics seriesMonarchy Central concepts MonarchMonarchismDivine right of kingsMandate of HeavenRoyal prerogative Types Abdication system Absolute Chinese Legalist Composite Constitutional Crowned republic Diarchy Dual Duchy Grand Dynastic union Elective Emirate Ethnarch Federal Hereditary Khanate Non-sovereign Pentarchy Personal union Popular Principality Real union Regency Coregency Self-proclaimed Signoria Tetrarch Triarchy Universal P...

UN goal to combat climate change Sustainable Development Goal 13Mission statementTake urgent action to combat climate change and its impacts by regulating emissions and promoting developments in renewable energyCommercial?NoType of projectNon-ProfitLocationGlobalFounderUnited NationsEstablished2015Websitesdgs.un.org Sustainable Development Goal 13 (SDG 13 or Global Goal 13) is to limit and adapt to human-caused climate change. It is one of 17 Sustainable Development Goals established by the U...

Eastern Iranian language of Afghanistan and Pakistan For other uses, see Pashto (disambiguation). PashtoپښتوPax̌tóThe word Pax̌tó written in the Pashto alphabetPronunciation[pəʂˈto], [pʊxˈto], [pəçˈto], [pəʃˈto]Native toAfghanistan, PakistanEthnicityPashtunsSpeakersL1: 44 million (2017–2021)[1]L2: 4.9 million (2022)[1]Language familyIndo-European Indo-IranianIranianEasternPashtoStandard forms Central Pashto Northern Pashto Southern Pashto...

2007 horror film by David Slade 30 Days of NightTheatrical release posterDirected byDavid SladeScreenplay by Steve Niles Stuart Beattie Brian Nelson Based on30 Days of Nightby Steve NilesBen TemplesmithProduced by Sam Raimi Robert Tapert Starring Josh Hartnett Melissa George Danny Huston Ben Foster Mark Boone Junior CinematographyJo WillemsEdited byArt JonesMusic byBrian ReitzellProductioncompanies Columbia Pictures Ghost House Pictures Dark Horse Entertainment Distributed bySony Pictures Rel...

مقاطعة قطانية شعار الإحداثيات 37°31′00″N 15°04′00″E / 37.516666666667°N 15.066666666667°E / 37.516666666667; 15.066666666667 تاريخ التأسيس 1860 تقسيم إداري البلد إيطاليا[1][2] التقسيم الأعلى صقلية العاصمة قطانية تاريخ الإلغاء 4 أغسطس 2015 التقسيمات الإدارية آت�...

Disambiguazione – Se stai cercando altri significati, vedi Roger Moore (disambigua). Roger Moore nel 1973 Sir Roger George Moore (Londra, 14 ottobre 1927 – Crans-Montana, 23 maggio 2017) è stato un attore britannico, noto per la partecipazione alle serie televisive Ivanhoe (1958-1959), Il Santo (1962-1969) e Attenti a quei due (1971-1972), nonché per essere stato il terzo interprete, dopo Sean Connery e George Lazenby, di James Bond nella serie ufficiale, con un totale di sette pellico...

Fictional character MissandeiA Song of Ice and Fire character Game of Thrones characterNathalie Emmanuel as MissandeiFirst appearance Literature: A Storm of Swords (2000) Television: Valar Dohaeris (2013) Last appearance Television: The Last of the Starks (2019) Created byGeorge R. R. MartinPortrayed byNathalie EmmanuelIn-universe informationGenderFemaleTitleQueen's Personal AdvisorOccupationAdvisor to the QueenRelatives Marselen[1] (brother) Mossador[1] (brother) NationalityN...
American politician This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (January 2019) (Learn how and when to remove this message) This article may need to be rewritten to compl...

XM395 Precision Guided Mortar Munition prototype at Fort Benning, Ga., Feb 2006 [1] XM395 Precision Guided Mortar Munition (PGMM) adalah mortar 120 mm yang dikembangkan oleh Alliant Techsystems. Berdasarkan Orbital ATK’s Precision Guidance Kit untuk proyektil artileri 155 mm, XM395 menggabungkan panduan GPS dan permukaan kontrol terarah ke dalam paket yang menggantikan standar fuzzy, mengubah bodi mortir 120 mm yang ada menjadi amunisi berpandu presisi. Amunisi XM395 ...

Энциклопедия Республики Марий Эл Автор Гл. редкол.: М. З. Васютин, Л. А. Гаранин и др.; Отв. лит. ред. Н. И. Сараева Жанр Справочно-энциклопедическое издание Язык оригинала русский Оригинал издан 2009 Издатель Галерия Выпуск 2009 Страниц 872 ISBN 978-5-94950-049-1 Энциклопедия Республик...