Trigonometria
|
Read other articles:

For other people named Peter Kirk, see Peter Kirk (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Peter Kirk English politician тАУ news ┬╖ newspapers ┬╖ books ┬╖ scholar ┬╖ JSTOR (February 2021) (Learn how and when to remove this template message) Sir Peter KirkLeader of the Conservatives i...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Anushka SharmaSharma pada tahun 2015Pekerjaan Model Aktris Tahun aktif2008 тАУ sekarang Anushka Sharma (Hindi: рдЕрдиреБрд╖реНрдХрд╛ рд╢р...

Kerajaan Ghassaniyah╪з┘Д╪║╪│╪з┘Ж┘К╪й220тАУ638 Bendera Spanduk perang Bani Ghassan selama Pertempuran Shiffin StatusNegara Klien Romawi TimurIbu kotaJabiyahBahasa yang umum digunakanArab KlasikAgama Kristen ArabPemerintahanMonarkiRaja тАв 220-265 Jafna ibn AmrтАв 632-638 Jabalah ibn al-Aiham Sejarah тАв Pembentukan 220тАв Klien Romawi Timur 473тАв Perang Yarmuk 636тАв Dianeksasi Kekhalifahan Rashidun 638 Didahului oleh Digantikan oleh Arabia Petraea...
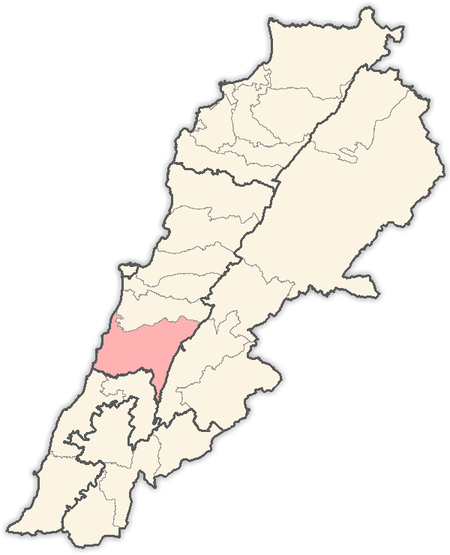
City in Mount Lebanon GovernorateMazraat el Daher Arabic: ┘Е╪▓╪▒╪╣╪й ╪з┘Д╪╢┘З╪▒CityMazraat el DaherLocation within LebanonCoordinates: 33┬░35тА▓N 35┬░30тА▓E / 33.583┬░N 35.500┬░E / 33.583; 35.500Country LebanonGovernorateMount Lebanon GovernorateDistrictChouf DistrictGovernmentElevation750 m (2,460 ft)Time zoneUTC+2 (EET) тАв Summer (DST)UTC+3 (EEST)Dialing code+961 Mazraat el Daher (Arabic: ┘Е╪▓╪▒╪╣╪й ╪з┘Д╪╢┘З╪▒) also spelled Maraat el Dahr, i...

╨Ю╨▒ ╤Н╨║╨╛╨╜╨╛╨╝╨╕╤З╨╡╤Б╨║╨╛╨╝ ╤В╨╡╤А╨╝╨╕╨╜╨╡ ╤Б╨╝. ╨Я╨╡╤А╨▓╨╛╤А╨╛╨┤╨╜╤Л╨╣ ╨│╤А╨╡╤Е (╤Н╨║╨╛╨╜╨╛╨╝╨╕╨║╨░). ╨е╤А╨╕╤Б╤В╨╕╨░╨╜╤Б╤В╨▓╨╛╨С╨╕╨▒╨╗╨╕╤П ╨Т╨╡╤В╤Е╨╕╨╣ ╨Ч╨░╨▓╨╡╤В ╨Э╨╛╨▓╤Л╨╣ ╨Ч╨░╨▓╨╡╤В ╨Х╨▓╨░╨╜╨│╨╡╨╗╨╕╨╡ ╨Ф╨╡╤Б╤П╤В╤М ╨╖╨░╨┐╨╛╨▓╨╡╨┤╨╡╨╣ ╨Э╨░╨│╨╛╤А╨╜╨░╤П ╨┐╤А╨╛╨┐╨╛╨▓╨╡╨┤╤М ╨Р╨┐╨╛╨║╤А╨╕╤Д╤Л ╨С╨╛╨│, ╨в╤А╨╛╨╕╤Ж╨░ ╨С╨╛╨│ ╨Ю╤В╨╡╤Ж ╨Ш╨╕╤Б╤Г╤Б ╨е╤А╨╕╤Б╤В╨╛╤Б ╨б╨▓╤П╤В╨╛╨╣ ╨Ф╤Г╤Е ╨Ш╤Б╤В╨╛╤А╨╕╤П ╤Е╤А╨╕╤Б╤В╨╕╨░╨╜╤Б╤В╨▓╨░ ╨Р╨┐╨╛╤Б╤В╨╛╨╗╤Л ╨е╤А╨╛╨╜╨╛╨╗╨╛╨│╨╕╤П ╤Е╤А╨╕╤Б╤В╨╕╨░╨╜╤Б╤В╨▓╨░ ╨а╨░╨╜╨...

Artikel ini menggunakan kata-kata yang berlebihan dan hiperbolis tanpa memberikan informasi yang jelas. Silakan buang istilah-istilah yang hiperbolis tersebut. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Logo Citra Maja Raya Citra Maja Raya[1] merupakan proyek kota terencana yang dibangun oleh Grup Ciputra di wilayah Kecamatan Maja, Kabupaten Lebak, Provinsi Banten. Proyek tersebut memiliki luas sebesar 2.600 hektar. Maja Lebak. Dalam master plan-nya, Citra Maj...

Questa voce sull'argomento stagioni delle societ├а calcistiche italiane ├и solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Associazione Sportiva Dilettantistica Sangiovannese 1927. Associazione Calcio SangiovanneseStagione 2008-2009Sport calcio Squadra Sangiovannese Allenatore Fabrizio Tazzioli poi Fabio Fraschetti Presidente Andrea Failli Seconda Divisione12┬║ posto nel girone B. Ma...

Stadion Nizhny Novgorod LokasiLokasiBetankura st., 1A, Nizhny Novgorod, RusiaKoordinat56┬░20тА▓15тА│N 43┬░57тА▓48тА│E / 56.33750┬░N 43.96333┬░E / 56.33750; 43.96333Koordinat: 56┬░20тА▓15тА│N 43┬░57тА▓48тА│E / 56.33750┬░N 43.96333┬░E / 56.33750; 43.96333Transportasi umum StrelkaKonstruksiMulai pembangunan2015Dibuat2018Biaya pembuatan17,9 miliar тВ╜Data teknisPermukaanGrassMasterKapasitas44,899 (Resmi)43,319 (Piala Dunia FIFA 2018)[1]Ukura...

Peta menunjukkan lokasi Plaridel Plaridel adalah munisipalitas yang terletak di provinsi Quezon, Filipina. Pada tahun 2010, munisipalitas ini memiliki populasi sebesar 12.140 jiwa dan 2.774 rumah tangga. Pembagian wilayah Secara administratif Plaridel terbagi menjadi 9 barangay, yaitu: Concepcion Duhat Ilaya Ilosong Tanauan Central (Pob.) Paang Bundok (Pob.) Paaralan or Pampaaralan (Pob.) M. L. Tumagay (Pob.) Pranala luar Philippine Standard Geographic Code Diarsipkan 2012-04-13 di Wayback Ma...

тАа ╨з╨╡╨╗╨╛╨▓╨╡╨║ ╨┐╤А╤П╨╝╨╛╤Е╨╛╨┤╤П╤Й╨╕╨╣ ╨Э╨░╤Г╤З╨╜╨░╤П ╨║╨╗╨░╤Б╤Б╨╕╤Д╨╕╨║╨░╤Ж╨╕╤П ╨Ф╨╛╨╝╨╡╨╜:╨н╤Г╨║╨░╤А╨╕╨╛╤В╤Л╨ж╨░╤А╤Б╤В╨▓╨╛:╨Ц╨╕╨▓╨╛╤В╨╜╤Л╨╡╨Я╨╛╨┤╤Ж╨░╤А╤Б╤В╨▓╨╛:╨н╤Г╨╝╨╡╤В╨░╨╖╨╛╨╕╨С╨╡╨╖ ╤А╨░╨╜╨│╨░:╨Ф╨▓╤Г╤Б╤В╨╛╤А╨╛╨╜╨╜╨╡-╤Б╨╕╨╝╨╝╨╡╤В╤А╨╕╤З╨╜╤Л╨╡╨С╨╡╨╖ ╤А╨░╨╜╨│╨░:╨Т╤В╨╛╤А╨╕╤З╨╜╨╛╤А╨╛╤В╤Л╨╡╨в╨╕╨┐:╨е╨╛╤А╨┤╨╛╨▓╤Л╨╡╨Я╨╛╨┤╤В╨╕╨┐:╨Я╨╛╨╖╨▓╨╛╨╜╨╛╤З╨╜╤Л╨╡╨Ш╨╜╤Д╤А╨░╤В╨╕╨┐:╨з╨╡╨╗╤О╤Б╤В╨╜╨╛╤А╨╛╤В╤Л╨╡╨Э╨░╨┤╨║╨╗╨░╤Б╤Б:╨з╨╡╤В╨▓╨╡╤А╨╛╨╜╨╛╨│╨╕╨╡╨Ъ╨╗╨░╨┤╨░:╨Р╨╝╨╜╨╕╨╛╤В╤Л╨Ъ╨╗╨░╨┤╨░:╨б╨╕╨╜╨░╨┐╤Б╨╕╨┤╤Л╨...

уБУуБошиШф║ЛуБпцдЬши╝хПпшГ╜уБкхПВшАГцЦЗчМоуВДхЗ║хЕ╕уБМхЕиуБПчд║уБХуВМуБжуБДуБкуБДуБЛуАБф╕НхНБхИЖуБзуБЩуАВхЗ║хЕ╕уВТш┐╜хКауБЧуБжшиШф║ЛуБоф┐бща╝цАзхРСф╕КуБлуБФхНФхКЫуБПуБауБХуБДуАВя╝ИуБУуБоуГЖуГ│уГЧуГмуГ╝уГИуБоф╜┐уБДцЦ╣я╝ЙхЗ║хЕ╕цдЬч┤в?: уВ│уГлуВп тАУ уГЛуГеуГ╝уВ╣ ┬╖ цЫ╕ч▒Н ┬╖ уВ╣уВлуГйуГ╝ ┬╖ CiNii ┬╖ J-STAGE ┬╖ NDL ┬╖ dlib.jp ┬╖ уВ╕уГгуГСуГ│уВ╡уГ╝уГБ ┬╖ TWLя╝И2017х╣┤4цЬИя╝Й уВ│уГлуВпуВТцЙУуБбцКЬуБДуБжф╜ЬуБгуБЯчУ╢уБоцаУ уВ│уГлуВпя╝ИцЬицаУуАБш...

2016 filmNational BirdTheatrical release posterDirected bySonia KennebeckProduced by Sonia Kennebeck Ines Hoffmann Kanna CinematographyTorsten LappEdited byMaxine GoedickeMusic byInsa RudolphProductioncompanies Ten Forward Films ITVS Corporation for Public Broadcasting NDR Deutscher Filmf├╢rderfonds Filmf├╢rderung Hamburg Schleswig-Holstein Kuratorium Junger Deutscher Film Distributed byFilmRiseRelease dates February 14, 2016 (2016-02-14) (Berlinale) November 11, ...

Powered industrial truck This article is about the powered industrial moving truck known as a forklift. For the manual pallet-moving tool sometimes called a pallet truck, see Pallet jack. This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (December 2023) ForkliftGeneral appearance of a typical forkliftClassificationPITIndustryVariousApplicationMultipl...

Japanese retired professional wrestler (born 1972) Katsushi TakemuraBorn (1972-08-21) August 21, 1972 (age 51)Joyo, Kyoto, JapanProfessional wrestling careerRing name(s)Great TakeMuga TakemuraKatsushi TakemuraTakemuraBilled height1.78 m (5 ft 10 in)Billed weight99 kg (218 lb)Trained byTatsumi FujinamiOsamu NishimuraDebutJuly 22, 1997RetiredJanuary 6, 2009 Katsushi Takemura (чл╣цЭС ш▒кц░П, Takemura Katsushi)[1] is a Japanese retired professional wrestler, ...

Athletics competitor, long distance runner, steeplechase, cross country Gaston RoelantsGaston Roelants in 1968Personal informationNationalityBelgianBorn (1937-02-05) 5 February 1937 (age 87)Opvelp, BelgiumHeight1.74 m (5 ft 9 in)Weight67 kg (148 lb)SportCountryBelgiumSportAthleticsEvent(s)Steeplechase, marathonClubDC LeuvenRetired1976Achievements and titlesPersonal best(s)3000 m Steeplechase тАУ 8:26.4 (1965)marathon тАУ 2:16:30 (1974) Medal record Representing &...

Shanghai Municipal People's Congress ф╕Кц╡╖х╕Вф║║ц░Сф╗гшбихдзф╝Ъ16th Shanghai Municipal People's CongressTypeTypeProvince-level people's congress Established16 August 1954LeadershipChairwomanHuang Lixin, CPC since January 24, 2024 Vice-chairpersonsZheng Gangmiao, CPCZhou Huilin, CPCZong Ming, CPCChen Jing, CPCZhang Quan, CPWDPXu Yisong, RCCK since January 28, 2018 Secretary-GeneralXie Jiangang, CPC since January 15, 2023 StructureSeats855 (include members of Standing Committee is 57)S...

Rise and ShineBerkas:Riseandshine.jpgAlbum studio karya Randy TravisDirilis15 Oktober 2002Direkam2001-2 at Seventeen Grand & The Sound Emporium - Nashville, TNGenreCountry, gospelDurasi45:09LabelWord/Warner Bros. Nashville/CurbProduserKyle LehningKronologi Randy Travis Inspirational Journey(2000)Inspirational Journey2000 Rise and Shine(2002) Worship & Faith(2003)Worship & Faith2003 Penilaian profesional Skor ulasan Sumber Nilai Allmusic [1] People (disukai)[2] ...

╪з┘Д╪г┘Е┘К╪▒ ╪╣╪и╪п ╪з┘Д┘Д┘З ╪и┘Ж ╪╣┘Д┘К ╪з┘Д╪╣╪и╪з╪│┘К ╪╣┘О╪и╪п┘П ╪з┘Д┘Д┘З ╪и┘Ж ╪╣┘О┘Д┘Р┘К┘П┘С ╪и┘Ж ╪╣┘О╪и╪п┘Р ╪з┘Д┘Д┘З ╪и┘Ж ╪з┘Д╪╣┘О╪и┘О┘С╪з╪│ ╪и┘Ж ╪╣╪и╪п ╪з┘Д┘Е┘П╪╖┘О┘С┘Д┘Р╪и ╪з┘Д┘З╪з╪┤┘Р┘Е┘К┘П┘С ╪з┘Д┘В┘П╪▒┘О╪┤┘К┘П┘С ┘Е╪╣┘Д┘И┘Е╪з╪к ╪┤╪о╪╡┘К╪й ╪з┘Д┘Е┘К┘Д╪з╪п 29 ╪░┘И ╪з┘Д╪н╪м┘О┘С╪й 102 ┘З┘А / 3 ┘К┘П┘И┘Д┘К┘И 721 ┘Е╪з┘Д╪н┘П┘Е┘О┘К┘Т┘Е┘О╪й╪М ╪з┘Д╪о┘Р┘Д╪з┘Б┘О╪й ╪з┘Д╪г┘П┘Е┘И┘К┘О┘С╪й ╪з┘Д┘И┘Б╪з╪й 147┘З┘А / 764 ┘Е (45 ╪│┘Ж╪й)╪и┘О╪║┘Т╪п┘О╪з╪п╪М ╪з┘Д╪о┘Р┘Д╪з┘Б┘О╪й ╪з┘Д╪╣┘О╪и┘О┘С╪з╪│┘Р┘К┘О┘С╪й ┘Е┘И╪з╪...

╪в┘Г╪▒┘И┘Ж ╪з┘Д╪з╪│┘Е ╪з┘Д╪▒╪│┘Е┘К (╪и╪з┘Д╪е┘Ж╪м┘Д┘К╪▓┘К╪й: Akron)тАП ╪з┘Д╪е╪н╪п╪з╪л┘К╪з╪к 41┬░04тА▓23тА│N 81┬░31тА▓04тА│W / 41.073055555556┬░N 81.517777777778┬░W / 41.073055555556; -81.517777777778 [1] ╪к╪з╪▒┘К╪о ╪з┘Д╪к╪г╪│┘К╪│ 1825 ╪к┘В╪│┘К┘Е ╪е╪п╪з╪▒┘К ╪з┘Д╪и┘Д╪п ╪з┘Д┘И┘Д╪з┘К╪з╪к ╪з┘Д┘Е╪к╪н╪п╪й[2][3] ╪з┘Д╪к┘В╪│┘К┘Е ╪з┘Д╪г╪╣┘Д┘Й ┘Е┘В╪з╪╖╪╣╪й ╪│╪з┘Е┘К╪к ╪╣╪з╪╡┘Е╪й ┘Д┘А ┘Е┘В╪з╪╖╪╣╪й ╪│╪з┘Е┘К╪к&...
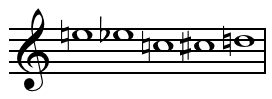
Set class redirects here. For the concept in set theory, see Class (set theory). Six-element set of rhythmic values used in Variazioni canoniche by Luigi Nono[1] A set (pitch set, pitch-class set, set class, set form, set genus, pitch collection) in music theory, as in mathematics and general parlance, is a collection of objects. In musical contexts the term is traditionally applied most often to collections of pitches or pitch-classes, but theorists have extended its use to other typ...










































































