Read other articles:

Kate LinderLinder pada peragaan busana pada Januari 2008Lahir2 November 1947 (umur 76)Pasadena, California, Amerika SerikatPekerjaanAktrisPramugariTahun aktif1973–sekarang Kate Linder (lahir 2 November 1947) adalah aktris asal Amerika Serikat, yang dikenal untuk perannya sebagai Esther Valentine dalam The Young and the Restless, yang ia perankan sejak tahun 1982.[1] Kehidupan dan karier Linder lahir di Pasadena, California, dan lulus dengan BA dalam seni teater Universita...

Ne doit pas être confondu avec Écriture musicale. Johann Sebastian Bach est l'archétype du musicien complet. Choriste jusqu'à la mue, claveciniste, organiste, violoniste, maître de chapelle. La quasi-totalité de ses œuvres est ancrée dans sa pratique instrumentale et répond aux nécessités de ses fonctions. Wolfgang Amadeus Mozart est considéré comme le premier compositeur indépendant, cherchant à libérer la composition musicale des exigences d'une fonction. Ludwig van Beethov...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. Min Tein memberikan surat kepercayaan kepada Presiden Rusia Vladimir Putin pada 16 November 2006. Min Thein adalah seorang diplomat Myanmar dan duta besar dari Myanmar untuk Rusia dari tahun 2006 sampai dengan tahun 2012. Dia memberikan surat kepercayaan...

Biografi ini tidak memiliki sumber tepercaya sehingga isinya tidak dapat dipastikan. Bantu memperbaiki artikel ini dengan menambahkan sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus.Cari sumber: Mickey Rourke – berita · surat kabar · buku · cendekiawan · JSTOR (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Mickey RourkeLahirPhilip Andre Rourke Jr.16 Se...

Swiss football club Football clubFC WilFull nameFussball Club Wil 1900Founded1900; 124 years ago (1900)GroundSportpark BergholzCapacity6,048ChairmanMaurice WeberManagerBrunello IacopettaLeagueSwiss Challenge League2022–235th of 10WebsiteClub website Home colours Away colours Current season FC Wil (Fussball Club Wil 1900) is a football club based in Wil, Switzerland. They play in the Sportpark Bergholz, which has a total capacity of 6,048. The club has consistently played i...

Ferdinand August Bebel Ferdinand August Bebel (lahir 22 Februari 1840 di Cologne, Jerman - meninggal 13 Agustus 1913 di Passugg, Swiss pada umur 73 tahun) adalah seorang tokoh dalam gerakan buruh Jerman dan revolusioner Marxis.[1][2] Bebel mendirikan Partai Demokrasi Sosial Jerman bersama Wilhelm Liebknecht pada tahun 1869.[1][2] Pada tahun 1858-1860, Bebel melakukan perjalanan ke Jerman selatan dan Austria sebagai pekerja harian.[2] Pada bulan Mei 1860...

Запрос «Пугачёва» перенаправляется сюда; см. также другие значения. Алла Пугачёва На фестивале «Славянский базар в Витебске», 2016 год Основная информация Полное имя Алла Борисовна Пугачёва Дата рождения 15 апреля 1949(1949-04-15) (75 лет) Место рождения Москва, СССР[1]...

2022 South Korean television series Good JobPromotional posterHangul굿잡Revised RomanizationGutjap Genre Mystery[1] Fantasy[1] Romance[1] Created byRyu Seung-jin[2]Developed byKT Studio Genie (planning)[3]Written by Kim Jeong-ae[4] Kwon Hee-kyung[4] Directed by Kang Min-gu[4] Kim Seong-jin[4] StarringJung Il-wooKwon Yu-riMusic byBaek Eun-wooCountry of originSouth KoreaOriginal languageKoreanNo. of episodes12[5]P...

Untuk tempat lain yang bernama sama, lihat Tanjung (disambiguasi). TanjungDesaNegara IndonesiaProvinsiJawa TimurKabupatenPamekasanKecamatanPademawuKode pos69381Kode Kemendagri35.28.02.2001 Luas42 km²Jumlah penduduk6,997 jiwaKepadatan....jiwa/km² Desa Tanjung adalah salah satu desa yang terletak di Kecamatan Pademawu, Pamekasan, Jawa Timur.[1] Sejarah Desa ASAL DAN ARTI NAMA DESA Tanjung berasal dari nama sebutan untuk daratan yang menjorok ke laut yang ketiga sisinya dikeliling...

穆罕默德·达乌德汗سردار محمد داود خان‎ 阿富汗共和國第1任總統任期1973年7月17日—1978年4月28日前任穆罕默德·查希爾·沙阿（阿富汗國王）继任穆罕默德·塔拉基（阿富汗民主共和國革命委員會主席團主席） 阿富汗王國首相任期1953年9月7日—1963年3月10日君主穆罕默德·查希爾·沙阿 个人资料出生(1909-07-18)1909年7月18日 阿富汗王國喀布尔逝世1978年4月28日(...

Soldats français utilisant un canon sans recul M18 de 57 mm contre de l'artillerie Viet Minh pendant la guerre d'Indochine (1953). Une arme sans recul est une arme individuelle ou montée sur des véhicules légers dont le fonctionnement repose sur le principe de deux canons tirant en sens opposés, le recul du tir étant compensé par l'éjection des gaz de la charge à l’arrière du fût. Le projectile n'est donc propulsé que par le coup initial (comme dans un canon classique) et pas pe...

4th District of Budapest For the football team, see Újpest FC. You can help expand this article with text translated from the corresponding article in Hungarian. (December 2009) Click [show] for important translation instructions. View a machine-translated version of the Hungarian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather t...

شركة البابطين للطاقة والاتصالاتشركة البابطين للطاقة والإتصالات (بالعربية)[1] الشعارمعلومات عامةالبلد  السعودية التأسيس 1955النوع مساهمة عامةالشكل القانوني شركة مساهمة — شركة عمومية محدودة المقر الرئيسي الرياض، ، السعوديةموقع الويب al-babtain.com.sa المنظومة الاقتصاديةال...

Asian flatbread This article is about the South and West Asian bread. For the Central Asian bread, see Tandyr nan. For the kibbutz, see Na'an. For other uses, see Naan (disambiguation). NaanAlternative namesNan, Noon, Paan, FaanRegion or stateIran, Indian subcontinent, Afghanistan, Indonesia, Malaysia, Myanmar, and the CaribbeanMain ingredientsFlour, yeast, salt, sugar, ghee, water  Media: Naan Naan is a leavened, oven-baked (usually using a tandoor) or tawa-fried flatbread. It is ch...

Antisemitic and racist laws enacted in 1935 in Nazi Germany For the set of guidelines for determining what constitutes a war crime, see Nuremberg principles. For the set of research ethics principles for human experimentation, see Nuremberg Code. Title page of the German government gazette Reichsgesetzblatt issue proclaiming the laws, published on 16 September 1935 (RGBl. I No. 100) Part of a series onDiscrimination Forms Institutional Structural Statistical Taste-based Attributes Age Caste C...

Chinese porcelain with scenes of Sydney For the Sydney suburb, see Punchbowl, New South Wales. Library punchbowl showing beach where Circular Quay is now located Museum punchbowl showing interior indigenous image common to both bowls The Sydney punchbowls, made in China during the Jiaqing Emperor's reign (1796–1820) over the mid-Qing dynasty, are the only two known examples of Chinese export porcelain hand painted with Sydney scenes and dating from the Macquarie era. The bowls were procured...

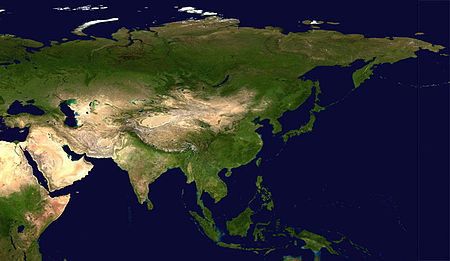
تعتبر آسيا أكبر القارات من حيث المساحة والسكان، فتشمل 30% من مجموع مساحة اليابسة، ويعيش عليها تقريبا ثلاثة أخماس سكان العالم، وتقع تقريبا في نصف الكرة الشمالي . يحدها شمالا المحيط القطبي الشمالي وبشرقه برينغ (مضيق) الجليدي. وفي الجنوب المحيط الهندي وبالغرب البحرين الأحمر و�...

ماركوس سينيسي (بالإسبانية: Marcos Senesi)‏    معلومات شخصية الميلاد 10 مايو 1997 (العمر 27 سنة)كونكورديا، انتري ريوس  الطول 1.85 م (6 قدم 1 بوصة) مركز اللعب مدافع الجنسية الأرجنتين  معلومات النادي النادي الحالي بورنموث الرقم 25 مسيرة الشباب سنوات فريق 2009–2016 سان لورينزو �...

Albert Oppel Información personalNacimiento 19 de diciembre de 1831 Hohenheim (Alemania) Fallecimiento 22 de diciembre de 1865 (34 años)Múnich (Reino de Baviera) EducaciónEducado en Universidad de Tubinga Supervisor doctoral Friedrich August von Quenstedt Información profesionalOcupación Paleontólogo y profesor universitario Empleador Universidad de Múnich Abreviatura en zoología Oppel Miembro de Academia de Ciencias de Baviera [editar datos en Wikidata] Carl Albert Oppel (...

  关于语法上的「數」，請見「数 (语法)」。 各种各样的数 基本 N ⊆ Z ⊆ Q ⊆ R ⊆ C {\displaystyle \mathbb {N} \subseteq \mathbb {Z} \subseteq \mathbb {Q} \subseteq \mathbb {R} \subseteq \mathbb {C} } 正數 R + {\displaystyle \mathbb {R} ^{+}} 自然数 N {\displaystyle \mathbb {N} } 正整數 Z + {\displaystyle \mathbb {Z} ^{+}} 小数 有限小数 无限小数 循环小数 有理数 Q {\displaystyle \mathbb {Q} } 代數數 A {...