Topología de Grothendieck
|
Read other articles:

The Uncanny CounterPoster promosiNama alternatifAmazing RumorHangul경이로운 소문 GenreFantasiMisteriCerita seruBerdasarkanAmazing Rumoroleh Jang Yi(Daum Webtoon)PengembangStudio DragonDitulis olehYeo Ji-naSutradaraYoo Seon-dongPemeranJo Byung-gyuYoo Jun-sangKim Se-jeongYeom Hye-ranNegara asalKorea SelatanBahasa asliKoreaJmlh. episode16ProduksiProduserYoo Sun-dongRumah produksiNeo EntertainmentDistributorOCN Netflix (internasional)Rilis asliFormat audioDolby DigitalRilis28 November 2020...

Part of a series onBritish law Acts of Parliament of the United Kingdom Year 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 ...

Disambiguazione – Geniere rimanda qui. Se stai cercando altri significati, vedi Geniere (disambigua). Questa voce o sezione sull'argomento militari è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti pi...

District of British India in Madras, British RajSouth CanaraDistrict of British IndiaCoordinates: 13°00′N 75°24′E / 13.00°N 75.40°E / 13.00; 75.40Empire British RajPresidencyMadrasArea • Total8,441 km2 (3,259 sq mi)Population (2001)[1] • Total3,005,897 • Density356.1/km2 (922/sq mi)Languages • AdministrativeEnglish • Spoken languagesTulu, Konkani, Kannada, Malayal...

Halaman ini berisi artikel tentang Provinsi di Belgia. Untuk Provinsi Limburg di Belanda, lihat Limburg (Belanda). LimburgProvinsi di Belgia BenderaLambang kebesaranKoordinat: 50°36′N 5°56′E / 50.600°N 5.933°E / 50.600; 5.933Koordinat: 50°36′N 5°56′E / 50.600°N 5.933°E / 50.600; 5.933Negara BelgiaWilayah FlandersIbukotaHasseltPemerintahan • GubernurJos LantmeestersLuas • Total2,422 km2 (0,93...

Santa BarbaraPoster teatrikalSutradaraDavid ChoProduserJo Eun-un Baek Jae-hoDitulis olehDavid ChoPemeranLee Sang-yoonYoon Jin-seoPenata musikKang Yoo-hyunSinematograferLee Hee-seobPenyuntingLee Sang-minPerusahaanproduksiFilm Company JoseEDistributor9ers EntertainmentTanggal rilis 17 Juli 2014 (2014-07-17) Durasi99 menitNegaraKorea SelatanBahasaKorea Santa Barbara (Hangul: 산타바바라) adalah film romansa Korea Selatan tahun 2014 yang dibintangi oleh Lee Sang-yoon dan Y...

National Women's Soccer League team in San Diego, California, United States Soccer clubSan Diego Wave FCFull nameSan Diego Wave Fútbol ClubNickname(s)Wave FCThe WaveFoundedJune 8, 2021; 2 years ago (2021-06-08)StadiumSnapdragon StadiumSan Diego, CaliforniaCapacity35,000OwnerRon BurklePresidentJill EllisHead coachCasey StoneyLeagueNational Women's Soccer League20231st of 12WebsiteClub website Home colors Away colors Current season San Diego Wave FC is an American professiona...

Questa voce o sezione tratta di una competizione calcistica in corso. Le informazioni possono pertanto cambiare rapidamente con il progredire degli eventi. Se vuoi scrivere un articolo giornalistico sull'argomento, puoi farlo su Wikinotizie. Non aggiungere speculazioni alla voce. Voce principale: Calcio Foggia 1920. Calcio FoggiaStagione 2023-2024Lo stadio Pino Zaccheria, campo di casa del Foggia. Sport calcio Squadra Foggia Allenatore Mirko Cudini (1ª-17ª) Massimiliano Olivieri (Ad I...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

Hereditary priest in Judaism For the Hawaiian religious practitioner, see Kahuna. For other uses, see Kohen (disambiguation). Part of a series of articles onPriesthood in Judaism KohenPresumption of priestly descentPriestly covenant RolesPriestly BlessingRedemption of the firstborn sonTzaraath (skin disease and mildew)The Torah instruction of the KohanimSacrificeIncense offeringBeth din shel KohanimPriestly divisions High PriestsAaronEleazarPhinehasEliAhimelechAbiathar(First Temple)Zado...

ملك القوط الشرقيين ثيوداهاد ملك القوط الشرقيين فترة الحكمم534-م536 تاريخ التتويج 534 م معلومات شخصية الميلاد 480توريسيوم الوفاة 719فيا فلامينيا مواطنة مملكة القوط الشرقيين الديانة اريوسية الحياة العملية المهنة حاكم اللغات لغة قوطية تعديل مصدري - تعديل ثيوداها�...

Luxembourgian tennis player Anne KremerCountry (sports) LuxembourgResidenceHesperangeBorn (1975-10-17) 17 October 1975 (age 48)Luxembourg CityHeight1.65 m (5 ft 5 in) [1]Turned proSeptember 1998RetiredAugust 2014PlaysRight-handed (two-handed backhand)Prize money$1,567,313SinglesCareer record496–418Career titles2 WTA, 5 ITFHighest rankingNo. 18 (29 July 2002)Grand Slam singles resultsAustralian Open2R (1999, 2001, 2002, 2003, 200...

اضغط هنا للاطلاع على كيفية قراءة التصنيف الفُطْرياتالعصر: الديڤوني المبكر - الحاضر 410–0 مليون سنة قك ك أ س د ف بر ث ج ط ب ن A collage of five fungi (clockwise from top left): a mushroom with a flat, red top with white-spots, and a white stem growing on the ground; a red cup-shaped fungus growing on wood; a stack of green and white moldy bread slices on a plate; a microscopic, spherical grey-col...

Roger LakeRoger LakeShow map of OregonRoger LakeShow map of the United StatesLocationEagle Cap Wilderness, Wallowa County, OregonCoordinates45°12′31″N 117°11′41″W / 45.2085°N 117.1948°W / 45.2085; -117.1948TypePondBasin countriesUnited StatesMax. length302 yd (276 m)Max. width113 yd (103 m)Average depth30 ft (9.1 m)Max. depth46 ft (14 m)Surface elevation7,360 ft (2,240 m) Roger Lake (also called Rogers...
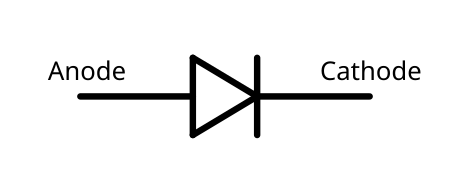
Diode bán dẫnMột số loại diode bán dẫnLoạiChủ độngChânanode và cathodeKý hiệu điệnD Diode bán dẫn (gọi tắt là diode) là một loại linh kiện bán dẫn chỉ cho phép dòng điện đi qua nó theo một chiều mà không theo chiều ngược lại.[1] Có nhiều loại diode bán dẫn, như diode chỉnh lưu thông thường, diode Zener, LED. Chúng đều có nguyên lý cấu tạo chung là một khối bán dẫn loại P ghép vớ...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (November 2021) (Learn how and when to remove this message)Aggregator of scientific data on biodiversity; data portal Global Biodiversity Information FacilityType of siteBiodiversity, natural historyArea servedWorldwideURLwww.gbif.orgCommercialNoLaunched2001; 23 years ago (2001)Current ...

Census-designated place in Rhode Island, United StatesGreenville, Rhode IslandCensus-designated placeLocation in Providence County and the state of Rhode Island.Coordinates: 41°52′36″N 71°33′12″W / 41.87667°N 71.55333°W / 41.87667; -71.55333CountryUnited StatesStateRhode IslandCountyProvidenceArea[1] • Total6.13 sq mi (15.88 km2) • Land5.56 sq mi (14.40 km2) • Water0.57 sq ...

American magician (1952–2021) David RothBorn(1952-03-13)March 13, 1952New York CityDiedJanuary 15, 2021(2021-01-15) (aged 68)Occupation(s)Magician, LecturerWebsitehttp://www.davidrothmagic.com/ David Roth (March 13, 1952 – January 13, 2021) was an American magician widely regarded as one of the world's greatest coin magicians.[1] Roth was an important contributor to Richard Kaufman's Coinmagic, an influential text on contemporary coin technique; his major work was chronicled ...

Museo di Palazzo Orsini UbicazioneStato Italia Localitàpalazzo Orsini IndirizzoPiazza Fortezza Orsini, 25 e Piazza Fortezza Orsini 25, 58017 Pitigliano Coordinate42°38′04.76″N 11°40′06.03″E42°38′04.76″N, 11°40′06.03″E CaratteristicheTipoArte sacra Istituzione1989 Apertura1º ottobre 1999 DirettoreLuca Caprini Visitatori11 177 (2022) Sito web Modifica dati su Wikidata · Manuale Il Museo di Palazzo Orsini[1] è un museo diocesano nella storica fortez...

Cet article est une ébauche concernant une commune du Loiret. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Le bandeau {{ébauche}} peut être enlevé et l’article évalué comme étant au stade « Bon début » quand il comporte assez de renseignements encyclopédiques concernant la commune. Si vous avez un doute, l’atelier de lecture du projet Communes de France est à votre disposition pour vous aider. Consultez également la page d’aide à l...

