Problema elastoplástico
|
Read other articles:

Syed Hasan Imamসৈয়দ হাসান ইমামBorn (1935-07-27) 27 July 1935 (age 88)Bardhaman, Bengal Presidency, British IndiaNationalityBangladeshiOccupation(s)Actor, film director, television directorSpouse Laila Hasan (m. 1965)[1]AwardsEkushey PadakIndependence Day Award Syed Hasan Imam (born 27 July 1935) is an actor, film director, television director and cultural personality in Bangladesh.[2] He earned Ekushey Padak (199...

Coppa Italia Lega Pro 2009-2010 Competizione Coppa Italia Lega Pro Sport Calcio Edizione 38ª Organizzatore Lega Italiana Calcio Professionistico Date dal 9 agosto 2009al 28 aprile 2010 Luogo Italia Partecipanti 90 Risultati Vincitore Lumezzane(1º titolo) Secondo Cosenza Cronologia della competizione 2008-2009 2010-2011 Manuale La Coppa Italia Lega Pro 2009-2010 è stata una competizione di calcio in Italia ad eliminazione diretta a cui hanno partecipato tutte le s...

Kubok Ukraïny 2004-2005Кубок України Competizione Kubok Ukraïny Sport Calcio Edizione 14ª Date dal 4 agosto 2004al 29 maggio 2005 Luogo Ucraina Partecipanti 64 Risultati Vincitore Dinamo Kiev(7º titolo) Secondo Šachtar Semi-finalisti DniproKryvbas Statistiche Miglior marcatore Diogo Rincón (6) Gol segnati 210 Cronologia della competizione 2003-2004 2005-2006 Manuale La Kubok Ukraïny 2004-2005 (in ucraino Кубок України?) fu la 14ª edizio...

American politician (born 1951) This article is about the politician. For the baseball coach, see Rob Bishop (baseball). Rob BishopRanking Member of the House Natural Resources CommitteeIn officeJanuary 3, 2019 – January 3, 2021Preceded byRaúl GrijalvaSucceeded byBruce WestermanChair of the House Natural Resources CommitteeIn officeJanuary 3, 2015 – January 3, 2019Preceded byDoc HastingsSucceeded byRaúl GrijalvaMember of the U.S. House of Representativesfro...

1984 United States Supreme Court caseChevron U.S.A. v. Natural Res. Def. CouncilSupreme Court of the United StatesArgued February 29, 1984Decided June 25, 1984Full case nameChevron U.S.A., Inc. v. Natural Resources Defense Council, Inc., et al.Docket nos.82-100582-124782-1591Citations467 U.S. 837 (more)104 S. Ct. 2778; 81 L. Ed. 2d 694; 21 ERC (BNA) 1049; 14 Envtl. L. Rep. 20,507; 52 U.S.L.W. 4845; 1984 U.S. LEXIS 118ArgumentOral argumentCase historyPriorNatural Resources Defense Council v. ...

Austroasiatic language spoken by the Mon in Burma and Thailand Monဘာသာမန်Pronunciation[pʰesa mɑn]Native toMyanmar Mon State Kayin State Tanintharyi Region RegionLower MyanmarEthnicityMonNative speakers800,000 – 1 million (2007)[1]Language familyAustroasiatic MonicMonWriting systemMon–Burmese (Mon alphabet)Official statusRecognised minoritylanguage in Myanmar ThailandLanguage codesISO 639-3Either:mnw – Modern Monomx&...

историческое государство ИмперияЯпонская империяяп. 大日本帝國 Флаг Императорская печать Гимн: «Кими га ё» Японская империя в 1942 году Япония (1870—1905) Колонии Оккупированные территории (1932—1945) ↓ ↓ 3 января 1868 (29 ноября 1890) — 2 сентяб...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

梅拉蒂·达伊瓦·奥克塔维亚尼Melati Daeva Oktavianti基本資料代表國家/地區 印度尼西亞出生 (1994-10-28) 1994年10月28日(29歲)[1] 印度尼西亞万丹省西冷[1]身高1.68米(5英尺6英寸)[1]握拍右手[1]主項:女子雙打、混合雙打職業戰績48勝–27負(女雙)109勝–56負(混雙)最高世界排名第4位(混雙-普拉文·喬丹)(2020年3月17日[2])現時世界排名第...

一中同表,是台灣处理海峡两岸关系问题的一种主張,認為中华人民共和国與中華民國皆是“整個中國”的一部份,二者因為兩岸現狀,在各自领域有完整的管辖权,互不隶属,同时主張,二者合作便可以搁置对“整个中國”的主权的争议,共同承認雙方皆是中國的一部份,在此基礎上走向終極統一。最早是在2004年由台灣大學政治学教授張亞中所提出,希望兩岸由一中各表�...

British ethnic group Ethnic group British Afro-Caribbean peopleDistribution by local authority in the 2011 censusTotal population United Kingdom: 628,296 – 0.9% (2021/22 Census) England: 619,419 – 1.1% (2021)[1] Scotland: 2,214 – 0.04% (2022)[a][2] Wales: 3,700 – 0.1% (2021)[1]Northern Ireland: 2,963 – 0.2% (2021)[b][3]Regions with significant populationsLondonBirminghamManchesterWolverhamptonNottinghamLutonLeedsBristol...

Indian agriculturist caste PatidarPatidar reservation agitationReligionsHinduismLanguagesGujaratiRegionPrincipally in Gujarat, but also some other states of India Patidar (Gujarati: Pāṭīdār[1]), formerly known as Kanbi (Gujarati: Kaṇabī[2]), is an Indian land-owning and peasant caste and community native to Gujarat. The community comprises at multiple subcastes, most prominently the Levas and Kadvas. They form one of the dominant castes in Gujarat. The title of Patidar...

1993 video gameThe TerminatorU.K. cover artDeveloper(s)Virgin GamesPublisher(s)Virgin GamesProducer(s)Erik YeoNeil YoungStephen Clarke-WillsonTom GibsonBarry Pringle Sr.Designer(s)Erik YeoTom TanakaDouglas CopeSilas WarnerProgrammer(s)Silas WarnerArtist(s)Nick BrutyWriter(s)Erik YeoJustin NorrComposer(s)Tommy TallaricoBrad FiedelBijan ShaheerJoey KurasTeknoMan of TeknologicSeriesTerminatorPlatform(s)Sega CDReleaseDecember 1993Genre(s)Platform, shoot 'em upMode(s)Single-player The Terminator i...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) بولينورماند 2014 تفاصيل السباقسلسلة35. بولينورماندمسابقاتطواف أوروبا للدراجات 2014 1.1كأس فرنسا لركوب ال�...

Indonesian model, Puteri Indonesia Lingkungan 2014 and Miss International Indonesia 2014 In this article, the surname is Rappa, her Sumatran patronymic surname; Pertiwi is her Sumatran matronymic surname. Elfin Pertiwi RappaRappa in KIPRAH PU magazine in 2014BornElfin Pertiwi Rappa (1995-09-23) 23 September 1995 (age 28)[1]Palembang, South Sumatera, IndonesiaAlma materSriwijaya University, Palembang, South Sumatera, IndonesiaHeight1.70 m (5 ft 7 in)Spouse Putr...
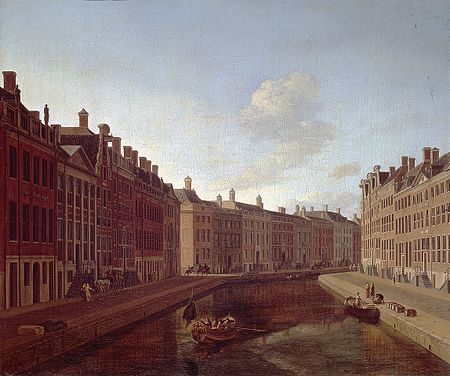
52°21′56″N 4°53′26″E / 52.36556°N 4.89056°E / 52.36556; 4.89056 Main article: Canals of Amsterdam The Gouden Bocht, 2008 The bend of the Herengracht in Amsterdam, 1685, Gerrit Adriaenszoon Berckheyde The Gouden Bocht (English: Golden Bend) is the most prestigious part of the Herengracht in Amsterdam, Netherlands, between Leidsestraat and Vijzelstraat. Until 1663 the Herengracht reached as far as the present Leidsegracht. From that year on, the fortification...

Asmara 2 Dunia Season 2Genre Drama Roman Fantasi Laga Misteri Ditulis olehTim Kreatif MKFSutradara Asep Khemunink Bobby Moeryawan Reza Fahlevi Pemeran Panji Saputra Andi Annisa Firstriana Aldila Arnold Leonard Brian Austin Isabelle Fry Charlotte Bellvania Ade Herlina Penggubah lagu temaAriel NoahLagu pembukaBintang di Surga oleh NoahLagu penutupBintang di Surga oleh NoahNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim2Jmlh. episode7ProduksiProduser eksekutifSubagio S.Produser Sonu ...

Computer games magazine This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Zzap!64 – news · newspapers · books · scholar · JSTOR (June 2021) (Learn how and when to remove this message) This article needs ...

Willem Dafoe Dafoe en el Festival Internacional de Cine de Venecia de 2024.Información personalNombre de nacimiento William James DafoeNacimiento 22 de julio de 1955 (69 años)Appleton (Wisconsin), Estados UnidosResidencia Appleton y Nueva York Nacionalidad Estadounidense e italianaFamiliaCónyuge Giada Colagrande (matr. 2005)Pareja Elizabeth LeCompte (1977-2004)Hijos Jack (1982)EducaciónEducado en Universidad de Wisconsin–Milwaukee (Drama)Appleton East High School Informaci...

American politician (born 1960) For other people named James Kelly, see James Kelly (disambiguation). James M. KellyKelly in August 2020Assistant Commandant for ReserveIn officeJune 14, 2021 – June 18, 2022Preceded byTodd C. Wiemers[1]Succeeded byMiriam L. LaffertyMember of the Maryland House of Delegatesfrom the 9B districtIn officeJanuary 11, 1995 – August 31, 2001Succeeded byMelissa J. Kelly Personal detailsBorn (1960-07-05) July 5, 1960 (age ...





















![{\displaystyle {\begin{cases}V=[H_{0}^{1}(\Omega )]^{3}\\Q=\{{\boldsymbol {\delta }}=(\delta _{ij})_{3\times 3}|\delta _{ij}=\delta _{ji}\in L^{2}(\Omega ),\ {\mbox{tr}}{\boldsymbol {\delta }}=0\}\\M=[L^{2}(\Omega )]^{m}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/417e0ab536b82a58a355e38b9f37e5a08cbd523c)




![{\displaystyle a(\mathbf {w} ,\mathbf {z} )=\int _{\Omega }[\mathbf {C} ({\boldsymbol {\varepsilon \mathbf {u} }}-{\tilde {\boldsymbol {\varepsilon }}}):({\boldsymbol {\varepsilon (\mathbf {v} )}}-\delta )+{\boldsymbol {\varepsilon }}:\mathbf {H} {\boldsymbol {\eta }}]\ d\mathbf {r} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/affc16eb05f4f3f70cc0038c8c6463a96c3bc768)


![{\displaystyle \int _{\Omega }D({\boldsymbol {\delta }},{\boldsymbol {\eta }})\ d\mathbf {r} \geq \int _{\Omega }D({\boldsymbol {\dot {\tilde {\varepsilon }}}},{\boldsymbol {\dot {\xi }}})\ d\mathbf {r} +\int _{\Omega }[\mathbf {C} ({\boldsymbol {\varepsilon (\mathbf {u} )}}-{\tilde {\boldsymbol {\varepsilon }}}):({\boldsymbol {\delta }}-{\dot {\tilde {\boldsymbol {\varepsilon }}}})-\mathbf {H} ({\boldsymbol {\xi }}):({\boldsymbol {\eta }}-{\boldsymbol {\dot {\xi }}})]\ d\mathbf {r} ,\quad \forall ({\boldsymbol {\delta }}-{\boldsymbol {\eta }})\in Z_{p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a6da43d1bffb7e17d2174855c5cf293064f58e7)


