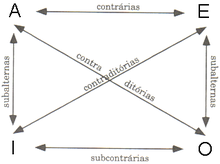
Primeros analíticos
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Prefektur Shimane 島根県PrefekturTranskripsi Jepang • Jepang島根県 • RōmajiShimane-ken BenderaLambangNegaraJepangWilayahChūgoku (San'in)PulauHonshuIbu kotaMatsuePemerintahan • GubernurMizoguchi ZenbeiLuas • Total6,707,95 km2 (2,58.995 sq mi)Peringkat18thPopulasi (September 1, 2016) • Total689.963 • Peringkat46th • Kepadatan10.285/km2 (26,640/sq mi)Kode ISO 3166JP-32Distrik...

Untuk informasi tentang merek ini di negara lainnya, lihat 3 (telekomunikasi). 3 IndonesiaTipeKartu SIM prabayar dan pascabayarTahun peluncuran29 Maret 2007ProdusenHutchison 3 Indonesia (2007-2022)Indosat Ooredoo Hutchison (2022-sekarang)KetersediaanTersediaSloganJaringan GSM-mu (2007-2012)Your Mobile Lifestyle Provider (2016-2020)Dunia Tri. Kekuatanku.(2020-2022)Ini Waktunya Kita. (2022-sekarang)Situs webtri.co.id PT Hutchison 3 IndonesiaNama dagang3 Indonesia3SebelumnyaPT Telindo Inti Nusa ...

Jordan 193KategoriFormula OneKonstruktorJordanPerancangGary Anderson (Technical Director) Mark Smith (Head of Mechanical Design)Andrew Green (Head of Structural Design)Pendahulu192Penerus194Spesifikasi teknis[1]SasisCarbon fibre and honeycomb composite structureSuspensi (depan)Double wishbones, pushrodSuspensi (belakang)Double wishbones, pushrodAxle trackFront: 1.690 mm (67 in)Rear: 1.610 mm (63 in)Wheelbase2.805 mm (110,4 in)MesinHart 1035, 3.499 cc...

Eragrostis curvula TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmonocotsKladcommelinidsOrdoPoalesFamiliPoaceaeSubfamiliChloridoideaeTribusEragrostideaeGenusEragrostisSpesiesEragrostis curvula Nees, 1841 Tata namaBasionimPoa curvula (en) lbs Eragrostis curvula adalah sebuah spesies rumput yang dikenal dengan nama umum weeping lovegrass. Nama-nama umum lainnya meliputi Boer lovegrass, curved lovegrass, Catalina lovegrass, dan African lovegrass. Tumbuhan tersebut berasal...

Untuk orang lain dengan nama yang sama, lihat Bill O'Reilly. Bill O'ReillyO'Reilly at the World Affairs Council of Philadelphia, September 30, 2010LahirWilliam James O'Reilly, Jr.10 September 1949 (umur 74)New York City, New York, A.S.Tempat tinggalManhasset, New YorkAlmamaterMarist College (BA)Universitas Boston (MA)Universitas Harvard (MPA)PekerjaanKolumnis, pengarang, tokoh televisi, tokoh radioTahun aktif1975–sekarangGaji$20.000.000 (2010)[1]Suami/istriMaureen E. McPhi...

Hochstadt a.Main Lambang kebesaranLetak Hochstadt a.Main di Lichtenfels NegaraJermanNegara bagianBayernWilayahOberfrankenKreisLichtenfelsMunicipal assoc.Hochstadt-MarktzeulnSubdivisions7 bydelePemerintahan • MayorThomas Kneipp (CSU)Luas • Total13,79 km2 (532 sq mi)Ketinggian281 m (922 ft)Populasi (2013-12-31)[1] • Total1.694 • Kepadatan1,2/km2 (3,2/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos96272Kode a...
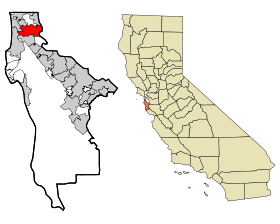
سووث سان فرانسيسكو الإحداثيات 37°39′22″N 122°25′32″W / 37.656111111111°N 122.42555555556°W / 37.656111111111; -122.42555555556 [1] تاريخ التأسيس 19 سبتمبر 1908 تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة سان ماتيو خصائص جغرافية المساحة 78.204956 �...

Artikel ini bukan mengenai Video Musik Terbaik (Grammy Award). Grammy Award untuk Film Musik TerbaikDeskripsiVideo musik bentuk panjang berkualitasNegaraAmerika SerikatDipersembahkan olehNational Academy of Recording Arts and SciencesDiberikan perdana1984Diberikan terakhir2017Situs webgrammy.com Grammy Award untuk Film Musik Terbaik (sampai 2012 dikenal sebagai Video Musik Bentuk Penjang Terbaik)[1][2] adalah sebuah penghargaan yang dipersembahkan di Grammy Award, sebuah acara...

County building in Truro, Cornwall, England Lys KernowLys Kernow in 2023LocationTruro, CornwallCoordinates50°15′36″N 5°04′09″W / 50.2600°N 5.0692°W / 50.2600; -5.0692Built1966ArchitectFrancis Kenneth Hicklin and Alan GrovesArchitectural style(s)Brutalist style Listed Building – Grade IIDesignated24 April 1998Reference no.1323700 Location of Lys Kernow in Cornwall Lys Kernow, known as New County Hall between 1966 and 2009, is a municipal facility at T...

Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari 59th Academy Awards di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan pene...

خالد بن عبد الله بن عبد الرحمن آل سعود معلومات شخصية الميلاد سنة 1937 الطائف تاريخ الوفاة 13 يناير 2021 (83–84 سنة)[1] مواطنة السعودية الزوجة الجوهرة بنت عبد العزيز آل سعود الأب عبد الله بن عبد الرحمن بن فيصل آل سعود عائلة آل سعود الحياة العملية المهنة �...

Cet article est une ébauche concernant les neurosciences et l’anatomie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. La chaîne sympathique droite et ses connexions avec les plexus thoracique, abdominal et pelvien Le plexus hypogastrique inférieur en anatomie humaine est un plexus nerveux situé dans le pelvis. Ses lames nerveuses sont situées latéralement de chaque côté du rectum. Le plexus hypogastr...

Bagian dari seriGereja Katolik menurut negara Afrika Afrika Selatan Afrika Tengah Aljazair Angola Benin Botswana Burkina Faso Burundi Chad Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Guinea Khatulistiwa Jibuti Kamerun Kenya Komoro Lesotho Liberia Libya Madagaskar Malawi Mali Maroko Mauritania Mauritius Mesir Mozambik Namibia Niger Nigeria Pantai Gading Republik Demokratik Kongo Republik Kongo Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland ...

Voce principale: Supercoppa di San Marino. Trofeo Federale 1999Trofeo Federale 1999 Competizione Trofeo Federale Sport Calcio Edizione 13ª Organizzatore FSGC Luogo San Marino Partecipanti 4 Formula torneo eliminazione diretta Risultati Vincitore Cosmos(3º titolo) Secondo Faetano Statistiche Incontri disputati 3 Gol segnati 8 (2,67 per incontro) Cronologia della competizione 1998 2000 Manuale Il Trofeo Federale 1999 è stato la 14ª edizione di tale competizione, e si è concluso...

Model 1216 Jenis Semi-automatic shotgun Negara asal United States Sejarah pemakaian Masa penggunaan 2011–present Sejarah produksi Tahun 2009 Produsen SRM Arms Biaya produksi $1,499–2,500 Diproduksi 2011–present Spesifikasi Berat 7.25 lbs (3.29 kg) Panjang 32.5 in (82.6 cm) Panjang laras 18 in (45.72 cm) Peluru 12 gauge Mekanisme Delayed blowback Amunisi 16 round detachable quad-tube revolver magazine Alat bidik Picatinny Rails for optics SRM Arms Model 1216 ada...

For the academic discipline, see Art history. Venus of Hohle FelsHorse painting from Lascaux cave systemMask of TutankhamunVenus de Milo, Alexandros of AntiochMona Lisa, Leonardo da VinciLes Demoiselles d'Avignon, Pablo Picasso History of art Periods and movements Prehistoric Ancient Medieval Pre-Romanesque Romanesque Gothic Renaissance Mannerism Baroque Rococo Neoclassicism Revivalism Romanticism Realism Pre-Raphaelites Modern Impressionism Symbolism Decorative Post-Impressionism Art Nouvea...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016) سيف الدين بشتاك الناصري معلومات شخصية تعديل مصدري - تعديل سيف الدين باشتاك الناصري هو الأمير سيف الدين �...

American leader in charitable work Louisa Lee SchuylerPortrait by Léon Bonnat (1879)Born(1837-10-26)October 26, 1837DiedOctober 10, 1926(1926-10-10) (aged 88)NationalityAmericanKnown forFounding the first nursing school in the United States Louisa Lee Schuyler (October 26, 1837 – October 10, 1926) was an early American leader in charitable work, particularly noted for founding the first nursing school in the United States. Charitable work During the Civil War, at the relatively y...

12th episode of the 9th season of South Park Trapped in the ClosetSouth Park episodeXenu as depicted in South Park, with a line onscreen mocking ScientologyEpisode no.Season 9Episode 12Directed byTrey Parker (credited as John Smith)Written byTrey Parker (credited as John Smith)Production code912Original air dateNovember 16, 2005 (2005-11-16)Episode chronology ← PreviousGinger Kids Next →Free Willzyx South Park season 9List of episodes Trapped in the Closet i...

Marouane Chamakh Informasi pribadiNama lengkap Marouane ChamakhTanggal lahir 10 Januari 1984 (umur 40)Tempat lahir Tonneins, PrancisTinggi 1,88 m (6 ft 2 in)[1]Posisi bermain PenyerangKarier junior1988–1994 Nérac1994–2000 Marmandais2000–2003 BordeauxKarier senior*Tahun Tim Tampil (Gol)2003–2010 Bordeaux 230 (56)2010–2013 Arsenal 40 (8)2013– → West Ham United (pinjaman) 3 (0)2013–2016 Crystal Palace 60 (7)2016 Cardiff City 2 (0)Tim nasional‡2003 ...