Optimización multiobjetivo
|
Read other articles:

Ziggurat of UrFasad ziggurat yang direkonstruksi.Lokasi di IrakLokasiTell el-Muqayyar, Provinsi Dhi Qar, IrakWilayahMesopotamiaKoordinat30°57′46″N 46°6′11″E / 30.96278°N 46.10306°E / 30.96278; 46.10306Koordinat: 30°57′46″N 46°6′11″E / 30.96278°N 46.10306°E / 30.96278; 46.10306JenisKuilBagian dariUrSejarahPendiriUr-NammuDidirikanKira-kira abad ke-21 SM Ziggurat Ur (kadang-kadang disebut Ziggurat Agung Ur; Sumeria E-te...

Indian Politician K. MohanMohan with his wife during their 50th wedding anniversary celebrationBorn(1926-03-14)14 March 1926Chennai, Tamil Nadu, IndiaDied24 August 2014(2014-08-24) (aged 89)Other namesPasamalar MohanOccupation(s)Art director, film producerYears active1950–2014SpouseShanthakumariChildren8 K. Mohanakrishnan (14 March 1926 – 24 August 2014) also known as Pasamalar Mohan, or simply K. Mohan, was an Indian film producer and art director. He entered the movi...

هذه المقالة عن الشاعر المصري أحمد شوقي. لمعانٍ أخرى، طالع أحمد شوقي (توضيح). أحمد شوقي علي معلومات شخصية اسم الولادة أحمد شوقي علي أحمد شوقي بك الميلاد 28 جمادى الآخرة 1285 هـ / 16 أكتوبر 1868 القاهرة، الخديوية المصرية الوفاة 1351 هـ / 14 أكتوبر 1932 (عن عمر يناهز 64) القاهرة، المملك...

Wakil Perdana MenteriLambang Pemerintah JepangPetahanaLowongsejak 4 Oktober 2021GelarTuan Wakil Perdana MenteriYang MuliaAnggotaKabinetDewan Keamanan NasionalDitunjuk olehPerdana Menteridibuktikan oleh KaisarMasa jabatanTidak ada istilah tetapPejabat perdanaKijuro ShideharaDibentuk3 Mei 1947SuksesiPertamaGaji¥20,916,000 Wakil Perdana Menteri Jepang (副総理code: ja is deprecated , Fuku-sōri) adalah pejabat tertinggi kedua dari cabang eksekutif pemerintah Jepang setelah Perdana Menter...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of European tornadoes and tornado outbreaks – news · newspapers · books · scholar · JSTOR (June 2011)...

Athenian military expedition to Sicily during the Peloponnesian War (415–413 BCE) For other sieges of Syracuse, see Siege of Syracuse (disambiguation). Sicilian Campaign redirects here. For World War II action, see Allied invasion of Sicily. Sicilian ExpeditionPart of the Peloponnesian WarDestruction of the Athenian army at Syracuse, as drawn in 1900Date415–413 BCLocationSicily, ItalyResult Spartan/Syracusan victory Athenian expeditionary force completely destroyedBelligerents Athens Alli...

SEMA6C المعرفات الأسماء المستعارة SEMA6C, SEMAY, m-SemaY, m-SemaY2, semaphorin 6C, Sema-Y معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 609294 MGI: MGI:1338032 HomoloGene: 7931 GeneCards: 10500 علم الوجود الجيني الوظيفة الجزيئية • semaphorin receptor binding• chemorepellent activity• neuropilin binding المكونات الخلوية • مكون تكاملي للغشاء• غشا�...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

† Стеллерова корова Муляж стеллеровой коровы в Лондонском музее естествознания Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстно�...

Chiesa d'IrlandaChiesa anglicana di Holmpatrick nella contea di Dublino (Irlanda)Classificazioneanglicana FondataXVI secolo Separata daChiesa cattolica AssociazioneComunione AnglicanaComunione di Porvoo DiffusioneIrlanda, Irlanda del Nord Forma di governoepiscopale SeparazioniChiesa metodista d'Irlanda Sito ufficialewww.ireland.anglican.org/ Modifica dati su Wikidata · Manuale La Chiesa d'Irlanda ((EN) Church of Ireland, (GA) Eaglais na hÉireann) è la provincia autonoma della Comunion...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

California wildfire redirects here. For the current fires in California, see 2024 California wildfires. Santa Ana winds in California expand fires and spread smoke over hundreds of miles, as in this October 2007 satellite image The Rim Fire consumed more than 250,000 acres (100,000 ha) of forest near Yosemite National Park, in 2013 This is a partial and incomplete list of California wildfires. California has dry, windy, and often hot weather conditions from spring through late autumn th...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يناير 2017) يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. ...

ChiLogoStato Italia Linguaitaliano Periodicitàsettimanale Generefemminili Fondazione3 marzo 1995 Sedevia privata Mondadori, 1 - Segrate (MI) EditoreGruppo Mondadori Diffusione cartacea154 919 (febbraio 2018) Diffusione digitale19 205 (febbraio 2018) DirettoreAlfonso Signorini (direttore editoriale)Massimo Borgnis (direttore responsabile) Sito webScheda editoriale Modifica dati su Wikidata · Manuale Copertina della rivista Chi, 21 febbraio 2018, Arnoldo Mondadori E...

1950 film When Men CheatDirected byCarl BoeseWritten byCarl BoeseCurth FlatowKároly Nóti (play)Kurt Schwabach (play)Produced byFrank CliffordStarringGrethe WeiserKurt SeifertJeanette SchultzeCinematographyHerbert KörnerEdited byUrsula NesteMusic byViktor AltmannProductioncompanyCordial-FilmDistributed byRing-FilmSascha Film (Austria)Release date 26 August 1950 (1950-08-26) Running time85 minutesCountryWest GermanyLanguageGerman When Men Cheat (German: Wenn Männer schwindeln...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Agustus 2020. Nine-Christine JönssonLahir(1926-06-08)8 Juni 1926Stockholm, SwediaMeninggal3 Januari 2011(2011-01-03) (umur 84)PekerjaanAktrisTahun aktif1946–1952 Nine-Christine Jönsson (8 Juni 1926 – 3 Januari 2011)[1] adalah se...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...
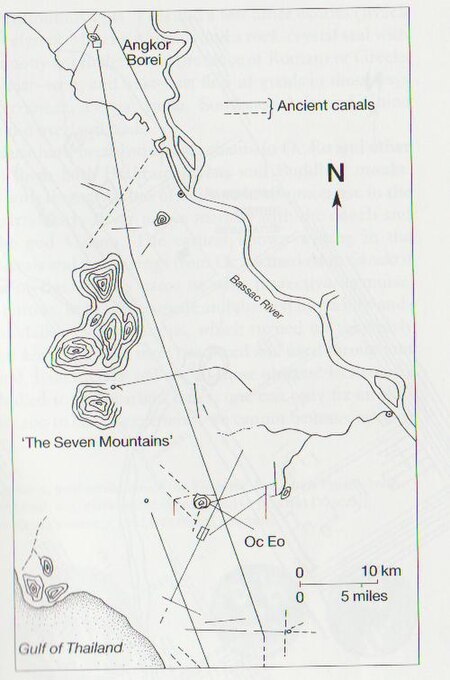
District in Takéo, CambodiaAngkor Borei អង្គរបូរីDistrictAngkor Borei Districtស្រុកអង្គរបូរីAngkor BoreiLocation in CambodiaCoordinates: 10°59′42″N 104°58′29″E / 10.99500°N 104.97472°E / 10.99500; 104.97472Country CambodiaProvinceTakéoTime zoneUTC+7 (ICT)ISO 3166 codeKH-2101 This article contains Khmer text. Without proper rendering support, you may see question marks, boxes, or other symbols instead ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) 1982 في إيطاليامعلومات عامةالسنة 1982 1981 في إيطاليا 1983 في إيطاليا تعديل - تعديل مصدري - تعديل ويكي بيانات سنوا...

Observable event For other uses, see Phenomena (disambiguation) and Phenomenal (disambiguation). The combustion of a match is an observable occurrence, or event, and therefore a phenomenon. A phenomenon (pl.: phenomena), sometimes spelled phaenomenon, is an observable event.[1] The term came into its modern philosophical usage through Immanuel Kant, who contrasted it with the noumenon, which cannot be directly observed. Kant was heavily influenced by Gottfried Wilhelm Leibniz in this ...










![{\displaystyle x^{*}=\left[x_{1}^{*},x_{2}^{*},\cdots ,x_{n}^{*}\right]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef67e4ca53f6aad306cc66d3418b953232d556bb)


![{\displaystyle f(x)=\left[f_{1}(x),f_{2}(x),\cdots ,f_{k}(x)\right]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ff48403d2e2bf117686f7ce68f2f32f5c46fb69)
![{\displaystyle x=\left[x_{1},x_{2},\cdots ,x_{n}\right]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bda93d89290f5b91614c8e8e15b57a84c424d3c)




