Nahariya
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Milan Jovanović Informasi pribadiNama lengkap Milan JovanovićTanggal lahir 18 April 1981 (umur 42)Tempat lahir Bajina Bašta, YugoslaviaTinggi 1,83 m (6 ft 0 in)[1]Posisi bermain PenyerangKarier junior VojvodinaKarier senior*Tahun Tim Tampil (Gol)1999–2003 Vojvodina 43 (10)2003–2004 Shakhtar Donetsk 6 (1)2004–2006 Lokomotiv Moscow 3 (0)2006–2010 Standard Liège 116 (52)2010–2011 Liverpool 10 (0)2011–2013 Anderlecht 68 (17)Total 246 (80)Tim nasional20...
Eggstätt. Eggstätt adalah kota yang terletak di distrik Rosenheim di Bayern, Jerman. Kota Eggstätt memiliki luas sebesar 24.29 km². Eggstätt pada tahun 2006, memiliki penduduk sebanyak 2.905 jiwa. lbsKota dan kotamadya di Rosenheim Albaching Amerang Aschau im Chiemgau Babensham Bad Aibling Bad Endorf Bad Feilnbach Bernau am Chiemsee Brannenburg Breitbrunn am Chiemsee Bruckmühl Chiemsee Edling Eggstätt Eiselfing Feldkirchen-Westerham Flintsbach Frasdorf Griesstätt Großkarolinenfe...

Sporting event delegationTunisia at the2004 Summer OlympicsIOC codeTUNNOCTunisian Olympic CommitteeWebsitewww.cnot.org.tn (in French)in AthensCompetitors54 in 14 sportsFlag bearer Noureddine Hfaiedh[1]Medals Gold 0 Silver 0 Bronze 0 Total 0 Summer Olympics appearances (overview)19601964196819721976198019841988199219962000200420082012201620202024 Tunisia competed at the 2004 Summer Olympics in Athens, Greece, from 13 to 29 August 2004. This was the nation's eleventh appearanc...
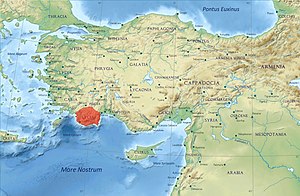
4th-century BC dynast of Lycia Perikles of LyciaPortrait of Perikles of Lycia, from his coinage. Circa 375-362 BCAllegianceLyciaYears of service375 to 362 BCRankKing of Lycia Location of Lycia. Anatolia/Asia Minor in the Greco-Roman period. The classical regions, including Lycia, and their main settlements Perikles (Perikle in Lycian), was the last known independent dynast of Lycia. A dynast of Limyra in eastern Lycia c. 375–362 BCE, he eventually ruled the entire country during ...

Ada usul agar artikel ini digabungkan ke Hutan. (Diskusikan) Ekosistem hutan mangrove Ekosistem hutan adalah salah satu sistem lingkungan paling kompleks di bumi yang memainkan peran penting dalam menjaga keseimbangan alam. Hutan adalah tempat tinggal bagi berbagai spesies flora dan fauna, serta menjadi sumber daya alam yang penting bagi manusia, seperti kayu, obat-obatan, dan air bersih. Namun, aktivitas manusia seperti penebangan hutan secara besar-besaran, pembakaran hutan, dan pertambanga...

Classical music radio station in Toronto CFMZ-FMToronto, OntarioBroadcast areaGreater Toronto AreaFrequency96.3 MHz (FM) (HD Radio)BrandingThe New Classical 96.3 FMProgrammingFormatClassical musicHD2: CFZMOwnershipOwnerZoomerMedia(MZ Media Inc.)Sister stationsCFMO-FM, CFMX-FM, CFZMHistoryFirst air date1988Former call signsCFMX-FM-1 (1988–2008)Call sign meaningCF Moses ZnaimerTechnical informationLicensing authorityCRTCClassC1ERP26,200 watts (average)60,000 watts (peak)HAAT283.6 meters (930&...

Unpaid police force in Jersey Officers of Saint Helier Honorary Police There is an Honorary Police (French: Police Honorifique) force in each of the twelve parishes of Jersey. Members of the Honorary Police are elected by the voters of the parish in which they serve, and are unpaid. Honorary Police officers have, for centuries, been elected by parishioners to assist the connétable of the parish to maintain law and order. Officers are elected as centeniers, vingteniers or constable's officers...

American cardiologist and author (1910–1980) Herman TarnowerBorn(1910-03-18)March 18, 1910New York City, U.S.DiedMarch 10, 1980(1980-03-10) (aged 69)Purchase, New York, U.S.Cause of deathGunshot woundsEducationSyracuse UniversityOccupation(s)Cardiologist, writerNotable workThe Complete Scarsdale Medical Diet Herman Tarnower (March 18, 1910 – March 10, 1980) was an American cardiologist and co-author (with Samm Sinclair Baker) of the bestselling diet book The Complete Scarsda...

銮披汶·頌堪แปลก พิบูลสงคราม第3任泰國總理任期1938年12月16日—1944年8月1日君主國王拉玛八世前任披耶帕凤侯爵继任寬·阿派旺第8任泰國總理任期1948年4月8日—1957年9月16日君主國王拉玛九世前任寬·阿派旺继任乃朴·沙拉信 个人资料出生貝·基達桑卡(1897-07-14)1897年7月14日 暹罗暖武里府逝世1964年6月11日(1964歲—06—11)(66歲) 日本神奈川縣相模原市国籍&#...

恩维尔·霍查Enver Hoxha霍查官方肖像照(摄于1980年代初)阿尔巴尼亚共产党中央委员会总书记任期1943年3月—1948年11月[1]前任無(首任)继任本人(劳动党中央委员会总书记)阿尔巴尼亚劳动党中央委员会总书记任期1948年11月—1954年7月[1]前任本人(共产党中央委员会总书记)继任本人(劳动党中央委员会第一书记)阿尔巴尼亚劳动党中央委员会第一书记任期1954�...
Thermococcus Klasifikasi ilmiah Domain: Archaea Kerajaan: Euryarchaeota Filum: Euryarchaeota Kelas: Thermococci Ordo: Thermococcales Famili: Thermococcaceae Genus: Thermococcus Spesies T. acidaminovorans T. aegaeus T. aggregans T. alcaliphilus T. atlanticus T. barophilus T. barossii T. celer T. chitonophagus T. coalescens T. fumicolans T. gammatolerans T. gorgonarius T. guaymasensis T. hydrothermalis T. kodakarensis T. litoralis T. marinus T. mexicalis T. pacificus T. peptonophilus T. profun...

Pelícanos Rango temporal: Rupeliense-Reciente, 28,1 Ma - 0 Ma PreЄ Є O S D C P T J K Pg N Pelícano común (Pelecanus onocrotalus) volando sobre la bahía de Walvis (Namibia). TaxonomíaReino: AnimaliaFilo: ChordataClase: AvesOrden: PelecaniformesFamilia: PelecanidaeRafinesque, 1815Género: PelecanusLinnaeus, 1758Especie tipo Pelecanus onocrotalusLinnaeus, 1758Especies 8 (ver texto) [editar datos en Wikidata] Los pelícanos (Pelecanus) son un género de aves acu�...

American politician and United States Navy sailor (1930–2021) Bill Brock18th United States Secretary of LaborIn officeApril 29, 1985 – October 31, 1987PresidentRonald ReaganPreceded byRaymond J. DonovanSucceeded byAnn McLaughlin8th United States Trade RepresentativeIn officeJanuary 23, 1981 – April 29, 1985PresidentRonald ReaganPreceded byReubin AskewSucceeded byClayton YeutterChair of the Republican National CommitteeIn officeJanuary 14, 1977 – January 20, ...

Not to be confused with Nomachi Station. Railway station in Takaoka, Toyama Prefecture, Japan Nōmachi Station能町駅Nōmachi Station in September 2018General informationLocation1438 Nōmachi, Takaoka-shi, Toyama-kenJapanCoordinates36°46′7.80″N 137°2′24.62″E / 36.7688333°N 137.0401722°E / 36.7688333; 137.0401722Operated by JR West JR Freight Line(s)■ Himi LineDistance4.1 km from TakaokaPlatforms1 island platformTracks2ConstructionStructure typeAt gradeO...

موقع قطاع غزة في الخريطة الإسرائيلية جزء من سلسلة مقالات حولدولة إسرائيل الجغرافيا أرض إسرائيل مناطق مدن النقل البحر الأبيض المتوسط البحر الأحمر البحر الميت التاريخ تاريخ مملكتي إسرائيل ويهوذا القديمتين تاريخ يهودي خط زمني صهيونية عليا تيودور هرتزل وعد بلفور الانتداب ا�...

Всеволод Мейерхольд (слева) на репетиции «Ревизора». Хлестаков — Эраст Гарин Театра́льный режиссёр — руководитель творческого процесса в театре, осуществляющий постановку драматического или музыкально-драматического (оперы, оперетты, мюзикла) произведения[1]...
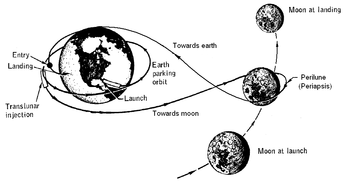
Type of free-return trajectory The trajectory followed by Apollo 13 Sketch of a circumlunar free return trajectory (not to scale). In orbital mechanics, a circumlunar trajectory, trans-lunar trajectory or lunar free return is a type of free return trajectory which takes a spacecraft from Earth, around the far side of the Moon, and back to Earth using only gravity once the initial trajectory is set. History The first spacecraft to fly a circumlunar trajectory was Luna 3. Circumlunar trajectori...

Untuk politikus, lihat Sanjay Kapoor (politikus). Untuk karakter EastEnders fiksi, lihat Sanjay Kapoor (EastEnders). Sanjay KapoorSanjay Kapoor di Peluncuran Proyek Batubara oleh Suzanne RoshanLahirChembur Mumbai, Maharashtra, IndiaKebangsaanIndiaPekerjaanPemeran dan produserTahun aktif1995–sekarangOrang tuaSurinder KapoorNirmal KapoorKerabatLihat Keluarga Kapoor Sanjay Kapoor adalah seorang pemeran dan produser asal India. Ia adalah putra dari produser Surinder Kapoor dan merupakan ad...

Miguel Ángel Castellón Rubio Miguel Ángel Castellón. Congreso de los Diputados 2021 Senador en las Cortes Generalespor Almería Actualmente en el cargo Desde el 23 de julio de 2023 Diputado en las Cortes Generalespor Almería 11 de noviembre de 2019-22 de julio de 2023 Diputado en el Parlamento de Andalucíapor Almería 25 de marzo de 2012-22 de marzo de 2015 Concejal del Ayuntamiento de Almería junio de 2015-mayo de 2019 Vicepresidente 2º de la Diputación Provincial de Almería junio ...

Convex quadrilateral with at least one pair of parallel sides Trapezoid (AmE)Trapezium (BrE)Trapezoid or trapeziumTypequadrilateralEdges and vertices4Area a + b 2 h {\displaystyle {\tfrac {a+b}{2}}h} Propertiesconvex Look up trapezoid in Wiktionary, the free dictionary. In geometry, a trapezoid (/ˈtræpəzɔɪd/) in North American English, or trapezium (/trəˈpiːziəm/) in British English,[1][2] is a quadrilateral that has one pair of parallel sides. The parallel sides are ...


