Mecánica hamiltoniana
|
Read other articles:

Questa voce sull'argomento contee del Wisconsin è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di VernonconteaLocalizzazioneStato Stati Uniti Stato federato Wisconsin AmministrazioneCapoluogoViroqua Data di istituzione1851 TerritorioCoordinatedel capoluogo43°33′25″N 90°53′19″W / 43.556944°N 90.888611°W43.556944; -90.888611 (Contea di Vernon)Coordinate: 43°33′25″N 90°53′19″W / 43...

Roddi commune di Italia Tempat categoria:Articles mancats de coordenades Negara berdaulatItaliaRegion di ItaliaPiedmontProvinsi di ItaliaProvinsi Cuneo NegaraItalia Ibu kotaRoddi PendudukTotal1.541 (2023 )GeografiLuas wilayah9,35 km² [convert: unit tak dikenal]Ketinggian284 m Berbatasan denganAlba La Morra Monticello d'Alba Santa Vittoria d'Alba Verduno SejarahSanto pelindungMaria Diangkat ke Surga Informasi tambahanKode pos12060 Zona waktuUTC+1 UTC+2 Kode telepon0173 ID ISTAT0041...

RED by HBODiluncurkan12 April 2010; 13 tahun lalu (2010-04-12)Ditutup1 Juli 2021; 2 tahun lalu (2021-07-01)PemilikHome Box Office, Inc.(WarnerMedia)SloganAsian Stories You LoveNegaraSingapuraBahasaInggris (utama)TiongkokJepangKoreaIndonesiaKantor pusatLorong Chuan New Tech Park, SingapuraSaluran seindukHBO, HBO Hits, CinemaxSitus webwww.redbyhbo.comTelevisi InternetHBO GoTonton langsungMola TV (Indonesia dan Timor Leste)Tonton langsung RED by HBO (sebelumnya Screen RED) adalah salur...

Anggaran Pendapatan dan Belanja Negara Tahun Anggaran 2015‹ 20142016 ›APBNDiusulkan15 Agustus 2014[4]Diajukan olehPresiden Susilo Bambang Yudhoyono[4]Diajukan kepadaDPR periode 2009-2014[4]Disetujui DPR29 September 2014[5]Disahkan Presiden14 Oktober 2014[6]Undang-UndangUndang-Undang Nomor 27 Tahun 2014[6]Total pendapatanRp1.793,6 triliun[6]Total belanjaRp2.039,5 triliun[6]DefisitRp245,9 triliun[6]APBN Peruba...

For other uses, see Beihai (disambiguation). Prefecture-level city in Guangxi, People's Republic of ChinaBeihai 北海BwzhaijPakhoiPrefecture-level cityBeihai Silver BeachLocation of Beihai in GuangxiCoordinates (Beihai government): 21°28′52″N 109°07′12″E / 21.481°N 109.120°E / 21.481; 109.120CountryPeople's Republic of ChinaRegionGuangxiMunicipal seatHaicheng DistrictArea • Prefecture-level city3,337 km2 (1,288 sq mi)Elevatio...

Confédération générale du travailLogo SegretarioSophie Binet Stato Francia Fondazione1895 SedeMontreuil, Parigi AbbreviazioneCGT IdeologiaAttualmenteSocialismoCorrenti interneComunismoStoricamenteComunismoAnarco-sindacalismo InternazionaleCSI, CES Basi confederali33 Iscritti653.222 (2017) TestataLa Nouvelle Vie ouvrière Sito webwww.cgt.fr/ Modifica dati su Wikidata · Manuale La Confédération générale du travail (CGT) è una confederazione sindacale francese creata il 23 se...

Il'ja Agapov Nazionalità Russia Altezza 174 cm Peso 73 kg Calcio Ruolo Difensore Squadra CSKA Mosca Carriera Giovanili Rubin Squadre di club1 2020-2021→ Neftechimik23 (1)2021-2022 Spartak-2 Mosca16 (1)2022-2023 Pari Nižnij Novgorod13 (0)2023- CSKA Mosca0 (0) Nazionale 2018-2019 Russia U-1814 (0)2019 Russia U-197 (1)2021 Russia U-212 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un ...

Не следует путать с Ираном — другим государством на Ближнем Востоке.Республика Иракараб. جُمْهُورِيَّة العِرَاق курд. کۆماری عێراق Флаг Герб Девиз: «الله أكبر»«Аллах велик» Гимн: «Моя Родина» Даты независимости 3 октября 1932 года (от Великобритании) Официальн...

Questa voce o sezione sull'argomento sovrani svedesi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Cristiano II di DanimarcaCristiano II ritratto da Lucas Cranach il VecchioRe di Danimarca e di NorvegiaStemma In carica22 luglio 1513 –20 gennaio 1523 Incoronazione11 giugno 1514 (Danimarca)20 luglio 1514 (Norvegia) PredecessoreGiovanni SuccessoreF...

1995 video gameDouble DragonDeveloper(s)Technōs Japan[a]Publisher(s)SNKTechnōs Japan(Neo Geo CD/PlayStation)PlayStation NetworkJP: HAMSTER CorporationNA: MonkeyPaw GamesProducer(s)Kazuyuki KurataDesigner(s)Minoru YamaguchiMuneki EbinumaProgrammer(s)Naoki KashiwabaraShinji HiraoTadamichi ObinataArtist(s)Akiko MaruyamaChihiro KushibeFujimi ŌnishiComposer(s)Chiaki IizukaFumio SuzukiKiyomi KataokaSeriesDouble DragonPlatform(s)Arcade, Neo Geo AES, Neo Geo CD, PlayStation, PlayStation N...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Sumur yang digali Zhao Tuo ketika menjabat sebagai bupati Longchuan, sumur ini dinamai Sumur Raja Yue (越王井) Zhao Tuo (Hanzi: 赵佗, Zhào Tuó, 230 SM – 137 SM) atau Triệu Đà dalam ejaan Vietnam adalah seorang jenderal Dinasti Qin yang kelak mendirikan kerajaan Nan Yue (Hanzi: 南越, bahasa Viet: Nam Việt) yang merupakan sebuah kerajaan kuno, terletak di perbatasan antara Tiongkok selatan dan Vietnam utara. Di tempat itu juga dia mendirikan Dinasti Zhao/ Trieu. Zhao dilahirkan...

Eurovision Song Contest 2022Country AzerbaijanNational selectionSelection processInternal selectionSelection date(s)Artist: 16 February 2022Song: 21 March 2022Selected entrantNadir RustamliSelected songFade to BlackSelected songwriter(s)Andreas Stone JohanssonAnderz WrethovSebastian SchubThomas StengaardFinals performanceSemi-final resultQualified (10th, 96 points)Final result16th, 106 pointsAzerbaijan in the Eurovision Song Contest ◄2021 • 2022 �...

Турки в Казахстане появились в 40-е годы XX века и за несколько десятилетий превратились в одну из самых многочисленных и быстрорастущих этнических общин республики. По переписи населения Казахстана 2021 года турков в стране было 85 478 человек[1]. Казахстанские турки в осн...
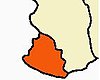
View of the hill from kanyakumari highway The Marundhuvazh Malai, a part of Sanjeevi hills is also known as the Marundhu Vazhum Malai/Maruthwamalai (the abode of medicinal herbs),[1][2] forms the part and the southernmost tip of the Western Ghats in Agasteeswaram taluk of Kanyakumari district of Tamil Nadu, India. People living in southern Kerala call it Maruthuva Mala. The hill stretches for more than a kilometer and reaches a height of 800 feet at the highest point, from wh...

Transportation system in Riyadh, Saudi Arabia Riyadh BusOverviewOwnerRoyal Commission for Riyadh CityLocaleRiyadhTransit typeBus rapid transitNumber of stations2,900+Websitewww.riyadhbus.saOperationBegan operation19 March 2023[1]Number of vehicles800+TechnicalSystem length1,900 km (1,180.61 mi) Riyadh Bus (Arabic: حافلات الرياض) is a 1184-mile comprehensive public bus service network system in Riyadh, Saudi Arabia.[2][3] Background The King Abdula...

جغرافيا جزر مارشال الحكومة البلد جزر مارشال تعديل مصدري - تعديل جزر المارشال، تتكون من سلسلتين أرخبيليتين تتكون من 30 جزيرة مرجانية و1152 جزيره، والتي تشكل مجموعتين متوازيتين - سلسلة «راتاك» شروق الشمس وسلسلة «راليك» غروب الشمس. وتقع جزر مارشال في شمال المحيط الهادئ و...
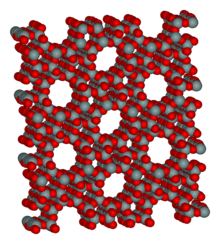
Kristalografi sinar-X bisa menentukan setiap atom pada zeolit, sebuah aluminosilikat. Kristalografi sinar-X adalah metode atau alat yang digunakan untuk menentukan struktur atom dan molekul sebuah kristal dengan cara mendifraksikan seberkas sinar-X ke segala arah. Dengan mengukur sudut dan intensitas difraksi sinar ini, kristalografer dapat menghasilkan gambar tiga dimensi mengenai kepadatan elektron di dalam kristal. Dari gambar kepadatan elektron ini, posisi rata-rata atom di dalam kristal ...
Reflexive and transitive binary relation This article is about binary relations. For the graph vertex ordering, see depth-first search. For purchase orders for unreleased products, see pre-order. For other uses, see Preorder (disambiguation). Quasiorder redirects here. For irreflexive transitive relations, see strict order. Transitive binary relations vte Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Total, Semiconnex Anti-reflexive E...

Contoh chicane dalam sirkuit olahraga otomotif. Chicane adalah kurva serpentin di jalan, ditambah dengan desain dari didikte oleh geografi. Chicane menambahkan putaran ekstra dan digunakan baik di olahraga otomotif seperti balap mobil / motor maupun di jalan raya konvensional untuk memperlambat lalu lintas demi keamanan. Misalnya, salah satu bentuk chicane adalah belokan pendek berbentuk dangkal yang mengharuskan pengemudi berbelok sedikit ke kiri dan sedikit demi sedikit melanjutkan perjalan...






![{\displaystyle {\begin{matrix}dH&=&\sum _{i}\left[\left({\partial H \over \partial q_{i}}\right)dq_{i}+\left({\partial H \over \partial p_{i}}\right)dp_{i}+\left({\partial H \over \partial t}\right)dt\right]\qquad \qquad \quad \quad \\\\&=&\sum _{i}\left[{\dot {q_{i}}}dp_{i}+p_{i}d{\dot {q_{i}}}-\left({\partial L \over \partial q_{i}}\right)dq_{i}-\left({\partial L \over \partial {\dot {q_{i}}}}\right)d{\dot {q_{i}}}-\left({\partial L \over \partial t}\right)dt\right].\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d442aa1497194c349c46913b1fa6a20e551be2b)



![{\displaystyle [F,G]=\sum _{i}\left[{\frac {\partial F}{\partial q_{i}}}{\frac {\partial G}{\partial p_{i}}}-{\frac {\partial F}{\partial p_{i}}}{\frac {\partial G}{\partial q_{i}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b1592e8a5de80fd4fda7a4b5230d788eb949ef0)
![{\displaystyle [,]:{\mathcal {F}}(\Gamma )\times {\mathcal {F}}(\Gamma )\to {\mathcal {F}}(\Gamma )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39214933ceafbfcc83cda908225604698129dc3)
![{\displaystyle [X,X]=0\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90781a6b2981745d5c6975158a5e66d0778c26f5)
![{\displaystyle [X,Y]=-[Y,X]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5a5717495d32f5d5438710cca822cc359cb2b75)
![{\displaystyle [X,C]=0\quad {\mbox{con}}\quad C={\mbox{cte.}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/693f81653ea41a4b59755562c28c4e5f41e2fc9e)
![{\displaystyle [\alpha X+\beta Y,Z]=\alpha [X,Z]+\beta [Y,Z]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4bcbc3b189d6f2b3fc47aa3eb9d0bf53db0948a)
![{\displaystyle [[X,Y],Z]+[[Z,X],Y]+[[Y,Z],X]=0\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e04950592f49b8bfd787dc9fb17158d1f337b81)
![{\displaystyle dX/dt=[X,H]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88e24740f75e35e5c5f0c16d13da3e7bb70a96e6)




















![{\displaystyle [F,G]=(i_{{\tilde {\omega }}(\mathrm {d} F)}\omega )(\mathrm {d} G)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9ebd51847643a1c277ab257953e2be2351ac4eb)
