Magnitud física
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Kathryn CarverCarver ca. 1924LahirAugust 24, 1899New York City, A.S.MeninggalJuly 17, 1947Elmhurst, New York, A.S.PekerjaanAktris Kathryn Carver (24 Agustus 1899 – 17 Juli 1947) adalah seorang aktris pada era film bisu yang berasal dari New York City. Biografi Carver bermain dalam film selama karir singkatnya dari 1925 hingga 1929. Dia bermain bersama Adolphe Menjou di Service For Ladies (1927) dan His Kehidupan Pribadi (1928). Dia menikah pertama kali dengan fotografer Ira L...

Caladi ulam Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Piciformes Famili: Picidae Genus: Dendrocopos Spesies: D. macei Nama binomial Dendrocopos macei(Vieillot, 1818) Caladi ulam (Latin: Dendrocopos maceicode: la is deprecated ) adalah spesies burung dari keluarga Picidae, dari genus Dendrocopos. Burung ini merupakan jenis burung pemakan serangga, larva, kalajengking, semut yang memiliki habitat di h...

Sur les autres projets Wikimedia : prospective, sur le Wiktionnaire La prospective, considérée comme une science de « l'homme à venir » par son créateur Gaston Berger[1], vise, par une approche rationnelle et holistique, à préparer le futur de l'être humain. Elle ne consiste pas à prévoir l'avenir (ce qui relevait de la divination et relève aujourd'hui de la futurologie[2]) mais à élaborer des scénarios possibles et impossibles dans leurs perceptions du moment s...

العلاقات الألمانية العمانية ألمانيا سلطنة عمان ألمانيا سلطنة عمان تعديل مصدري - تعديل العلاقات الألمانية العمانية هي العلاقات الثنائية التي تجمع بين ألمانيا وسلطنة عمان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: ...

مارك فيرو (بالفرنسية: Marc Ferro) مارك فيرو سنة 2012 معلومات شخصية اسم الولادة (بالفرنسية: Marc Roger Ferro) الميلاد 24 ديسمبر 1924 الدائرة الثامنة في باريس الوفاة 21 أبريل 2021 (96 سنة) [1][2] سن جرمن آن له[3][4]، وميزون-لافيت سبب الوفاة مرض فيروس �...

American politician For the United States Representative from Indiana, see James F. McDowell. For the Wisconsin State Assemblyman, see James F. McDowell (Wisconsin politician). For New Zealand politician, see James McDowall. James McDowellDaguerreotype portrait of Governor McDowellMember of the U.S. House of Representativesfrom Virginia's 11th districtIn officeMarch 6, 1846 – March 3, 1851Preceded byWilliam TaylorSucceeded byJohn Letcher29th Governor of VirginiaIn officeJanuary...

American politician John Paul Verree John Paul Verree (March 9, 1817 – June 27, 1889) was a Republican member of the U.S. House of Representatives from Pennsylvania. John Paul Verree was born at Verree Mills, on Pennypack Creek, near what is now Fox Chase Station, Philadelphia. He engaged in the manufacture of iron and subsequently was a dealer in edged tools and also in iron and steel. He was a member of the select council of Philadelphia from 1851 to 1857, serving as president from 1853 t...

OctopussyOctopussy film posterSutradaraJohn GlenProduserAlbert R. BroccoliDitulis olehIan Fleming (stories)SkenarioGeorge MacDonald FraserMichael G. WilsonRichard MaibaumPemeranMaud AdamsLouis JourdanSteven BerkoffDesmond LlewelynKristina WaybornRobert BrownRoger MoorePenata musikJohn BarrySinematograferAlan HumeDistributorMGM/UA Entertainment Co.Tanggal rilis6 Juni 1983 (Britania Raya)10 Juni 1983 (AS)Durasi131 min.NegaraBritania RayaBahasaInggrisHindiJermanRusiaAnggaran$35,000,000Pend...

Con il termine idrato, usato nella chimica inorganica e nella chimica organica, si indica una sostanza contenente acqua. Lo stato chimico dell'acqua varia ampiamente tra gli idrati, alcuni dei quali vennero così etichettati ancor prima che la loro struttura chimica venisse compresa. Con il termine idrato, in passato, si indicavano spesso gli idrossidi, particolarmente degli elementi alcalini e alcalino terrosi, ad esempio l'idrato di potassio, ottenibili chimicamente per aggiunta di acqua al...

Yossi SaridLahir(1940-10-24)24 Oktober 1940Tempat lahirRehovot, Mandat PalestinaMeninggal dunia4 Desember 2015(2015-12-04) (umur 75)Knesset8, 9, 10, 11, 12, 13, 14, 15, 16Faksi yang diwakili di Knesset1974–1984Alignment1984–1992Ratz1992–2006MeretzJabatan menteri1992–1996Menteri Lingkungan Hidup1999–2000Menteri Pendidikan Yossi Sarid (Ibrani: יֹוסֶף יֹוסִי שָׂרִיד; 24 Oktober 1940 – 4 Desember 2015) adalah seorang komentator berita dan mantan poli...

Pre-Roman tribe in Iberia Location of the tribe of the Autrigones. The Autrigones were a pre-Roman tribe that settled in the north of the Iberian Peninsula, in what today is the western Basque Country (western regions of Biscay and Álava) and northern Burgos and the East of Cantabria, Spain. Their territory limited with the Cantabri territory at west, the Caristii at east, the Berones at the southeast and the Turmodigi at the south. It is discussed whether the Autrigones were Celts, theory s...

Venezuelan baseball player and coach In this Spanish name, the first or paternal surname is Vizquel and the second or maternal family name is González. Baseball player Omar VizquelVizquel with the Chicago White Sox in 2011ShortstopBorn: (1967-04-24) April 24, 1967 (age 57)Caracas, VenezuelaBatted: SwitchThrew: RightMLB debutApril 3, 1989, for the Seattle MarinersLast MLB appearanceOctober 3, 2012, for the Toronto Blue JaysMLB statisticsBatting avera...

Ken SugimoriNama dalam bahasa asli(ja) 杉森建 BiografiKelahiran27 Januari 1966 (58 tahun)Fukuoka KegiatanSpesialisasiDesain permainan Pekerjaanilustrator, sutradara film, character designer, Perancang grafis, mangaka, penulis skenario Karya kreatifKarya terkenal Pokémon Ken Sugimori (杉森建code: ja is deprecated , Sugimori Ken) (lahir 27 Januari 1966) adalah seorang ilustrator dan seniman asal Jepang yang banyak dikenal masyarakat dunia sebagai sutradara seni dari l...

15°50′S 72°08′W / 15.83°S 72.13°W / -15.83; -72.13[1] Huambo volcanic field is a volcanic field in Peru. Andahua-Orcopampa lies north-northeast and Sabancaya east of Huambo,[1] east of the Rio Colca.[2] The town of Huambo lies between the two fields.[3] The northern part of the field was active 700 BCE ± 50 years, forming a large lava flow field and a cinder cone Cerro Keyocc. The southern part of the field contains other cinder...
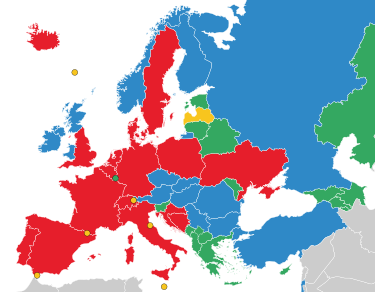
Лига наций УЕФА 2020/2021англ. 2020–21 UEFA Nations League Время проведения 3 сентября – 17 ноября 2020 (групповой этап) 6 — 10 октября 2021 (плей-офф) Место проведения Италия (плей-офф) Число участников 55 Призовые места Победитель Франция (1-й раз) Второе место Испания Третье мес...

Women's ice hockey club championship tournament This article is about the European women's ice hockey club championship. For the nations championship, see IIHF European Women Championships. This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (July 2018) (Learn how and when to remove this message) European Women Champions CupTourn...

أسماء بنت أبي بكر معلومات شخصية الميلاد 27 ق.هـ / 595ممكة الوفاة 73 هـ/ 692مكة اللقب ذات النطاقين الديانة الإسلام الزوج الزبير بن العوام الأولاد عبد الله بن الزبيرعروة بن الزبيرالمنذر بن الزبير الأب أبو بكر الصديق الأم قتيلة بنت عبد العزى إخوة وأخوات عائشة بنت أبي بكر،...

Abiu Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Asterid Ordo: Ericales Famili: Sapotaceae Subfamili: Chrysophylloideae Genus: Pouteria Spesies: P. caimito Nama binomial Pouteria caimitoRadlk. Sinonim[1] Guapeba glazioveana Pierre Krugella hartii Pierre Labatia pedunculata Willd. Labatia tovarensis Engl. Lucuma glazioviana Pierre ex Glaz. Lucuma hartii Hemsl. Lucuma huallagae Standl. ex ...

Disambiguazione – Fallaci rimanda qui. Se stai cercando il giornalista, vedi Bruno Fallaci. Oriana Fallaci Oriana Fallaci (Firenze, 29 giugno 1929 – Firenze, 15 settembre 2006) è stata una giornalista, scrittrice e partigiana italiana. Partecipò giovanissima alla Resistenza italiana e fu la prima donna italiana ad andare al fronte in qualità di inviata speciale. Fu una grande sostenitrice della rinascita culturale ellenica e conobbe le più importanti personalità di questa, t...

بلدة باترفيلد الإحداثيات 44°17′53″N 84°55′14″W / 44.2981°N 84.9206°W / 44.2981; -84.9206 [1] تقسيم إداري البلد الولايات المتحدة التقسيم الأعلى مقاطعة ميساوكي خصائص جغرافية المساحة 36.0 ميل مربع ارتفاع 345 متر عدد السكان عدد السكان 473 (1 أبريل 2020)[2] ...























