Estrategia evolutivamente estable
|
Read other articles:

La statua del Chollima a Pyongyang simboleggia la velocità con cui la società coreana dovrebbe progredire.Il movimento Chollima (천리마운동?, 千里馬運動?, ch'ŏllima undongMR) era un movimento stacanovista sponsorizzato dallo stato nordcoreano che promuoveva un rapido sviluppo economico. Esso iniziò nel 1956 o nel 1958[1] e fu caratterizzato principalmente dal culto della personalità nei confronti del presidente Kim Il-sung. Indice 1 Storia 1.1 Il movimento 1.2 Conseguen...

Conférence sur la sécurité et la coopération en Europe Acte final d'Helsinki1er août 1975 Données clés Date 1973 à 1994 Lieu Europe (+ États-Unis et Canada) Cause Renforcement de la sécurité, du respect des droits de l'homme et des échanges Chronologie 3 juillet 1973 Ouverture de la CSCE à Helsinki 1er août 1975 Signature Acte final d'Helsinki juin 1985 Échec de la réunion sur les droits de l'homme septembre 1986 Adoption de mesures de confiance et de sécurité (MDCS) janvie...

Questa voce o sezione sugli argomenti festività religiose e Ebraismo non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Yom KippurEbrei aschenaziti in preghiera nella Sinagoga durante lo Yom Kippur, di Maurycy Gottlieb (1878)Nome originaleיום הכיפורים Tiporeligiosa Data10 di Tishri ReligioneEbrai...

Ne doit pas être confondu avec Homininae, Hominini ou Hominina. Hominidae Les huit espèces actuelles d'hominidés, classées en lignes par genres : Humains, Chimpanzés, Bonobos , Gorilles (de l'Ouest, de l'Est) et Orang-outans (de Bornéo, de Sumatra, de Tapanuli).Classification ITIS Règne Animalia Embranchement Chordata Classe Mammalia Ordre Primates Sous-ordre Haplorrhini Infra-ordre Simiiformes Micro-ordre Catarrhini Super-famille Hominoidea FamilleHominidaeGray, 1825 Sous-famill...

US Army general (born 1961) Not to be confused with Darrell K. Williams. Darryl A. WilliamsOfficial portrait, 2022Born (1961-06-22) 22 June 1961 (age 62)Alexandria, Virginia, United StatesAllegianceUnited StatesService/branchUnited States ArmyYears of service1983–presentRankGeneralCommands held United States Army Europe and Africa Allied Land Command United States Military Academy United States Army Warrior Transition Command United States Army Africa Battles/warsGulf WarIraq WarA...

Bourbach-le-Hautcomune Bourbach-le-Haut – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Alto Reno ArrondissementThann CantoneCernay AmministrazioneSindacoJoël Mansuy TerritorioCoordinate47°48′N 7°02′E / 47.8°N 7.033333°E47.8; 7.033333 (Bourbach-le-Haut)Coordinate: 47°48′N 7°02′E / 47.8°N 7.033333°E47.8; 7.033333 (Bourbach-le-Haut) Superficie6,95 km² Abitanti415[1] (2020) Densità59,71 ab./km² Co...

Coppa d'Albania 2023-2024Kupa e Shqipërisë 2023-2024 Competizione Kupa e Shqipërisë Sport Calcio Edizione 72ª Organizzatore FSHF Date dal 27 settembre 2023al maggio 2024 Luogo Albania Partecipanti 44 Cronologia della competizione 2022-2023 2024-2025 Manuale La Kupa e Shqipërisë 2023-2024 è la 72ª edizione della coppa nazionale albanese, iniziata il 27 settembre 2022 e con termine nel maggio 2024. L'Egnatia è la squadra campione in carica, avendo conquistato il trofeo ...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: SMA Negeri 1 Jetis Bantul – berita · surat kabar · buku · cendekiawan · JSTORSMA NEGERI 1 JETISInformasiDidirikan20 November 1984JenisNegeriAkreditasiAMaskotEuphoria longanaKepala SekolahDra. Yati Utami ...

Untuk bangsawan abad ke-12 silakan lihat Egas Moniz António Egas MonizLahirAntónio Caetano de Abreu Freire Egas Moniz(1874-11-29)29 November 1874Avanca, Estarreja, PortugalMeninggal13 Desember 1955(1955-12-13) (umur 81)LisbonKebangsaanPortugalAlmamaterUniversity of CoimbraDikenal atasPrefrontal leucotomy; Cerebral angiographyPenghargaanPenghargaan Nobel dalam Fisiologi atau Kedokteran, 1949Karier ilmiahBidangNeurologisInstitusiUniversity of Coimbra (1902); University of Lisbon (1921-19...

Second season of the Blue Exorcist anime television series Season of television series Blue Exorcist: Kyoto SagaSeason 2The first DVD volume of Blue Exorcist: Kyoto SagaNo. of episodes12ReleaseOriginal networkMBS TVOriginal releaseJanuary 7 (2017-01-07) –March 24, 2017 (2017-03-24)Season chronology← PreviousSeason 1 Next →Shimane Illuminati Saga List of episodes Blue Exorcist: Kyoto Saga (Japanese: 青の祓魔師(エクソシスト) 京都不浄王篇, Hepb...
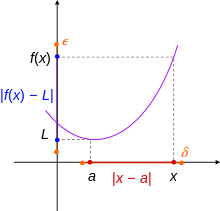
Mathematical function Functionx ↦ f (x) History of the function concept Examples of domains and codomains X {\displaystyle X} → B {\displaystyle \mathbb {B} } , B {\displaystyle \mathbb {B} } → X {\displaystyle X} , B n {\displaystyle \mathbb {B} ^{n}} → X {\displaystyle X} X {\displaystyle X} → Z {\displaystyle \mathbb {Z} } , Z {\displaystyle \mathbb {Z} } → X {\displaystyle X} X {\displaystyle X} → R {\displaystyle \mathbb {R} } , R {\displaystyle \mathbb {R} } → X {\...

Species of New World monkey Brown spider monkey[1] Brown spider monkey at Barquisimeto Zoo, Venezuela Conservation status Critically Endangered (IUCN 3.1)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Primates Suborder: Haplorhini Infraorder: Simiiformes Family: Atelidae Genus: Ateles Species: A. hybridus Binomial name Ateles hybridusI. Geoffroy, 1829 Brown spider monkey range in green The brown spider monke...

Field-equations in general relativity Einstein equation redirects here. For the equation E = m c 2 {\displaystyle E=mc^{2}} , see Mass–energy equivalence. General relativity G μ ν + Λ g μ ν = κ T μ ν {\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\kappa }T_{\mu \nu }} Introduction HistoryTimelineTests Mathematical formulation Fundamental concepts Equivalence principle Special relativity World line Pseudo-Riemannian manifold Phenomen...

No debe confundirse con Suprema Corte de Justicia de la Nación, tribunal de México. Corte Suprema de Justicia de la Nación Palacio de Justicia de la Nación, sede de la Corte Suprema de Justicia de la Nación Argentina.LocalizaciónPaís República ArgentinaLocalidad Buenos AiresCoordenadas 34°36′08″S 58°23′10″O / -34.6022, -58.3861Información generalSigla CSJNJurisdicción Todo el país (competencia originaria y derivada)Tipo corte supremaSede Talcahuano 550 CAB...

Study of the hospitality industry This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (July 2011) (Learn how and when to remove this message) This article needs additional citations for verifi...

Voce principale: Associazione Sportiva Dilettantistica Fidelis Andria 1928. Associazione Sportiva Fidelis AndriaStagione 1995-1996Sport calcio Squadra Fidelis Andria Allenatore Giuliano Sonzogni (1ª-36ª) Stefano Boggia (37ª-38ª) Presidente Giuseppe Fuzio Serie B17º posto. Retrocessa in Serie C1 Coppa ItaliaPrimo turno Maggiori presenzeCampionato: M. Giampaolo e Masolini (36) Miglior marcatoreCampionato: Masolini (7) StadioStadio degli Ulivi 1994-1995 1996-1997 Si invita a seguire i...

Species of bird Rufous-crowned bee-eater Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Coraciiformes Family: Meropidae Genus: Merops Species: M. americanus Binomial name Merops americanusMüller, 1776 Synonyms Merops viridis americanus The rufous-crowned bee-eater (Merops americanus) is a species of bird in the family Meropidae. It is endemic to the Philippines, where it is w...

British reality television series This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Britain's Next Top Model – news · newspapers · books · scholar · JSTOR (May 2016) (Learn how and when to remove this message) Britain's Next Top ModelAlso known asBritain & Ireland's Next Top Model(2011–13)GenreReality te...

Barra do Rocha Município do Brasil Símbolos Bandeira Brasão de armas Hino Gentílico barra-rochense Localização Localização de Barra do Rocha na BahiaLocalização de Barra do Rocha na Bahia Barra do RochaLocalização de Barra do Rocha no Brasil Mapa de Barra do Rocha Coordenadas 14° 12′ 39″ S, 39° 36′ 07″ O País Brasil Unidade federativa Bahia Municípios limítrofes Ipiaú, Ubatã, Gongogi, Ibirataia e Nova Ibiá Distância até a capital 432 ...

Byzantine emperor from 1118 to 1143 For other people named John Komnenos, see John Komnenos (disambiguation). John II KomnenosEmperor and Autocrat of the RomansMosaic of John II at the Hagia SophiaByzantine emperorReign15 August 1118 – 8 April 1143Coronation1092 as co-emperorPredecessorAlexios I KomnenosSuccessorManuel I KomnenosCo-emperorAlexios the YoungerBorn13 September 1087Constantinople, Byzantine Empire(now Istanbul, Turkey)Died8 April 1143(1143-04-08) (aged 55)Ci...