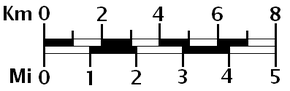
Escala (cartografía)
|
Read other articles:

AftershineInformasi latar belakangNama lainTengah Malam(sebelum menjadi Aftershine)AsalKabupaten Sleman, Daerah Istimewa YogyakartaGenrePop JawadangdutkoploTahun aktif2019–sekarangAnggota Hasan Aftershine Andika Permana Putra Hedo Anka Pindo Zulian Achmad Yuniarto Agus Nugroho Yuriko Andrianta Aftershine (sebelumnya bernama Tengah Malam) adalah sebuah grup musik bergenre pop Jawa dan koplo asal Indonesia. Grup musik ini berasal dari Kabupaten Sleman, Daerah Istimewa Yogyakarta. Anggota Nama...

Becky ChambersKebangsaanAmerika SerikatGenreFiksi ilmiahKarya terkenalThe Long Way to a Small, Angry PlanetA Closed and Common OrbitWebsitewww.otherscribbles.com Becky Chambers adalah seorang pengarang fiksi ilmiah asal Amerika. Novel debut tahun 2014nya adalah The Long Way to a Small, Angry Planet, dan disusul oleh sebuah sekuel, A Closed and Common Orbit, pada 2016. Novel-novelnya mengambil latar alam fiksi yang disebut Galactic Commons. Karya ketiganya, yang berjudul, Record of a Spac...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2016. Ini adalah daftar maskapai penerbangan yang saat ini beroperasi di Chad. Maskapai penerbangan IATA ICAO Tanda panggil Air Afrique Horizon - TPK TCHAD-HORIZON Mid Express Tchad - - - Toumaï Air Tchad 9D THE TOUMAI AIR Lihat pula Daftar maskapai penerbang...

Прямая кишкалат. rectum Прямая кишка толстого кишечника обозначена красным Схема поперечного сечения прямой кишки и ануса, наружного и внутреннего сфинктеров, кавернозных тел Кровоснабжение superior rectal artery[d] Венозный отток superior rectal vein[d] Лимфа Inferior mesenteric lymph nodes[d] Каталоги MeS...

Quad Studios Nashville was a four-studio recording facility established as Quadrafonic Sound Studio in 1971 on Music Row in Nashville, Tennessee, US. The studio was the location of numerous notable recording sessions, including Neil Young's Harvest, Jimmy Buffett's Margaritaville, Joan Baez' The Night They Drove Old Dixie Down, and Dobie Gray's Drift Away. The studio's location has been the home of Sienna Recording Studios since 2014. History Quadrafonic Sound Studio Established by session m...

National forest in California, US Klamath National ForestLittle Elk Lake in Klamath National ForestMap of the United StatesLocationSiskiyou County, California / Jackson County, OregonNearest cityYreka, CaliforniaCoordinates41°30′01″N 123°20′00″W / 41.50028°N 123.33333°W / 41.50028; -123.33333Area1,737,774 acres (7,032.52 km2)Governing bodyU.S. Forest ServiceWebsiteKlamath National Forest Klamath National Forest is a 1,737,774-acre (2,715 ...

BrO2 redirects here. For the oxyanion with the formula BrO−2, see Bromite. Bromine dioxide Names IUPAC name Bromine dioxide Identifiers CAS Number 21255-83-4 Y 3D model (JSmol) Interactive image ChemSpider 4574124 N PubChem CID 5460629 InChI InChI=1S/BrO2/c2-1-3 NKey: SISAYUDTHCIGLM-UHFFFAOYSA-N NInChI=1/BrO2/c2-1-3Key: SISAYUDTHCIGLM-UHFFFAOYAZ SMILES O=Br=O Properties Chemical formula BrO2 Molar mass 111.903 g/mol[1] Appearance unst...

For other uses, see Mecklenburg (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mecklenburg – news · newspapers · books · scholar · JSTOR (July 2019) (Learn how and when to remove this message) Historical region of Germany Historical region of GermanyMecklenburgHistorical region of Germany ...

Keuskupan ShimogaDioecesis Shimogaensisಶಿವಮೊಗ್ಗ ಧರ್ಮಕ್ಷೇತ್ರKatedral Hati KudusLokasiNegaraIndiaProvinsi gerejawiBangaloreMetropolitBangaloreStatistikLuas21.405 km2 (8.265 sq mi)Populasi- Total- Katolik(per 2010)7.822.00021,006 (0.3%)InformasiRitusRitus LatinKatedralKatedral Hati Kudus di ShimogaPelindungHati Kudus YesusKepemimpinan kiniPausFransiskusUskupFrancis Serrao SJUskup agungPeter MachadoSitus webSitus Web Keuskup...

Viral video The correct title of this article is Evo Moment #37. The omission of the # is due to technical restrictions. Evo Moment #37 (Daigo Parry) at the Evolution Championship Series 2004 (Evo 2004)Screenshot of Evo Moment #37, showing Umehara (Ken) parrying the first hit of Wong (Chun-Li)'s Super Art.VenueCalifornia State Polytechnic UniversityLocationPomona, CaliforniaDateAugust 1, 2004CompetitorsDaigo Umehara, Justin Wong Evo Moment #37, or the Daigo Parry, is a portion of a Stree...

Protein-coding gene in humans PHOX2AIdentifiersAliasesPHOX2A, ARIX, CFEOM2, FEOM2, NCAM2, PMX2A, paired like homeobox 2aExternal IDsOMIM: 602753 MGI: 106633 HomoloGene: 31296 GeneCards: PHOX2A Gene location (Human)Chr.Chromosome 11 (human)[1]Band11q13.4Start72,239,077 bp[1]End72,245,664 bp[1]Gene location (Mouse)Chr.Chromosome 7 (mouse)[2]Band7 E2|7 54.66 cMStart101,467,520 bp[2]End101,471,933 bp[2]RNA expression patternBgeeHumanMouse (orth...

Company This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (June 2020) (Learn how and when to remove this message) DWF Group Ltd.HeadquartersLondon, England, UKNo. of offices31No. of attorneys1,100No. of employees4,886Major practice areasGeneral Practice (see below)Key peopleJonathan Bl...

Not to be confused with 2023 Rolex Shanghai Masters Tennis Tournament. 2023 invitational snooker tournament 2023 Shanghai MastersTournament informationDates11–17 September 2023 (2023-09-11 – 2023-09-17)VenueShanghai Grand StageCityShanghaiCountryChinaOrganisationWorld Snooker TourFormatNon-ranking eventTotal prize fund£825,000Winner's share£210,000Highest break Ronnie O'Sullivan (ENG) (143)FinalChampion Ronnie O'Sullivan (ENG)Runner-up Luca B...

ملعب الحمدانيةمعلومات عامةالمنطقة الإدارية حلب البلد سوريا[1] التشييد والافتتاحالافتتاح الرسمي 1986 الاستعمالالمستضيف نادي الحرية السوريالمالك الحكومة السوريةمعلومات أخرىالطاقة الاستيعابية 18٬000 الأرضية عشبيةالموقع الجغرافيالإحداثيات 36°11′08″N 37°07′13″E / ...

Campagna della Malesiaparte del teatro del Pacifico della seconda guerra mondialeTruppe giapponesi avanzano a Kuala LumpurData8 dicembre 1941 - 31 gennaio 1942 LuogoMalesia britannica EsitoVittoria strategica dei giapponesi, che spianarono la strada per la conquista di Singapore Modifiche territorialiConquista giapponese della Malesia Schieramenti Impero britannico Regno Unito Australia Kuomintang della Malesia[1] Giappone Thailandia Comandanti Arthur Percival Henry Gor...

William ScottGladys Brockwell dan Scott dalam White Lies (1920)Lahir1 Agustus 1893Minneapolis, Minnesota, Amerika SerikatMeninggal22 Agustus 1967 (usia 74)Los Angeles, California, Amerika SerikatPekerjaanPemeranTahun aktif1913–1934 William Scott (1 Agustus 1893 – 22 Agustus 1967) adalah seorang pemeran Amerika Serikat pada era film bisu. Ia tampil dalam 90 film antara 1913 dan 1934. Ia lahir di Minneapolis, Minnesota dan meninggal di Los Angeles, California.[1]...

Cycling at the Olympics Men's cycling team time trialat the Games of the XVII OlympiadVenuePacific Ocean Lane, Rome100.00 km (62.1 mi)Date26 August 1960Competitors126 from 32 nationsWinning time2:14:33.53Medalists Antonio Bailetti, Ottavio Cogliati, Giacomo Fornoni, Livio Trapè Italy Gustav-Adolf Schur, Egon Adler, Erich Hagen, Günter Lörke Germany Viktor Kapitonov, Yevgeny Klevtsov, Yury Melikhov, Aleksei Petrov Soviet Union← 19561964 ...

Anti-semitic laws passed by the German government in the late 1930s The Nuremberg Laws of 1935 as published in the Reichsgesetzblatt. Anti-Jewish legislation in pre-war Nazi Germany comprised several laws that segregated the Jews from German society and restricted Jewish people's political, legal and civil rights. Major legislative initiatives included a series of restrictive laws passed in 1933, the Nuremberg Laws of 1935, and a final wave of legislation preceding Germany's entry into World ...

Food Macaroni soupMacaroni soup in Hong KongTypeSoupPlace of originItalyMain ingredientsMacaroniVariationsPasta e fagioli Macaroni soup is soup that includes macaroni. The food is a traditional dish in Italy, and is sometimes served with beans, which is known as pasta e fagioli,[1] and was also included in Mrs. Beeton's Book of Household Management, where the connection with Italy is mentioned and the dish includes Parmesan cheese.[2] In the early 19th century, macaroni soup w...

1666 painting by Johannes Vermeer For the 1910 Thanhouser film, see Mistress and Maid (film). Mistress and Maid (c. 1667) by Johannes Vermeer Mistress and Maid (Dutch: Dame en dienstbode) is an oil-on-canvas painting produced by Johannes Vermeer c. 1667. It portrays two women, a mistress and her maid, as they look over the mistress' letter. The painting displays Vermeer's preference for yellow and blue, female models, and domestic scenes. It is now in the Frick Collection in New York City. Ar...