Error cuadrático medio
|
Read other articles:

InvestopediaURLInvestopedia.comTipeKeuangan & investasiRegistration (en)Tidak adaLangueInggrisPemilikIACService entry (en)Juni 1999Peringkat Alexa▼ 931 (February 2016[update])[1] Investopedia adalah situs pendidikan investasi yang berpusat di New York City. Situs web ini dirintis oleh Cory Janssen dan Cory Wagner pada bulan Juni 1999.[2] Tahun 2007, situs ini dibeli oleh perusahaan penerbit Amerika Serikat, Forbes,[3] yang menjualnya ke ValueClick tahun 2...

لمعانٍ أخرى، طالع جيمس غوردون (توضيح). جيمس غوردن James Gordon الظهور الأول باتمان الظهور الأول في القصص المصورة باتمان المبتكر نيل هاميلتون، وبنيامين ماكنزي، ولايل تالبوت، وبات هنغل، وغاري أولدمان، وجي كي سيمونز، وجيفري رايت الصوت بواسطة بالعربية...

Untuk Paus Markus dalam Gereja Koptik, lihat Paus Markus (disambiguasi). Paus Markus (lahir di Roma, Italia) adalah seorang Paus, pemimpin Gereja Katolik Roma, uskup Roma dari 18 Januari 336 hingga 7 Oktober 336. Didahului oleh:Silvester I PausJanuari - Oktober 336 Diteruskan oleh:Julius I lbs Paus Gereja Katolik Daftar paus grafik masa jabatan orang kudus Nama Paus Abdikasi Paus Paus emeritus Antipaus Paus terpilih Abad ke-1s.d. ke-4 Petrus Linus Anakletus Klemens I Evaristus Aleksander...

العلاقات الأرمينية الموزمبيقية أرمينيا موزمبيق أرمينيا موزمبيق تعديل مصدري - تعديل العلاقات الأرمينية الموزمبيقية هي العلاقات الثنائية التي تجمع بين أرمينيا وموزمبيق.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: و�...
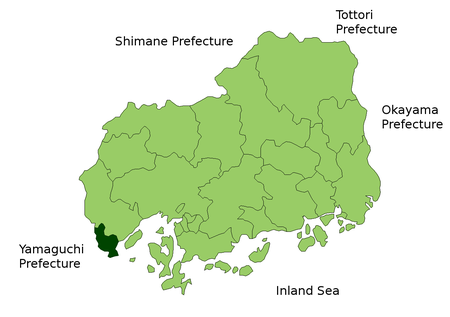
Ōtake 大竹市KotaNegaraJepangWilayahChugokuPrefekturHiroshimaPemerintahan • Wali KotaYoshirō IriyamaLuas • Total78,55 km2 (30,33 sq mi)Populasi • Total29,691 • Kepadatan378/km2 (980/sq mi)Lambang • PohonKuroganemochi • BungaSatsuki AzaleaZona waktuUTC+9 (JST)Situs webkota Ōtake Ōtake (大竹市code: ja is deprecated , ōtake-shi) adalah sebuah kota yang berada di ujung barat dari Prefektur Hirosh...

Emilio Aguinaldo, who led the Philippine Revolution against Spain, and Manuel L. Quezon, President of the autonomous Commonwealth of the Philippines under the United States Early polities in what is now the Philippines were small entities known as barangays, although some larger states were established following the arrival of Hinduism and Islam through regional trade networks. The arrival of Spanish settlers began a period of Spanish expansion which led to the creation of the Captaincy Gene...

This article is about the Major League Baseball player. For other people with the same name, see Sam Thompson (disambiguation). American baseball player (1860–1922) Baseball player Sam ThompsonRight fielderBorn: (1860-03-05)March 5, 1860Danville, Indiana, U.S.Died: November 7, 1922(1922-11-07) (aged 62)Detroit, Michigan, U.S.Batted: LeftThrew: LeftMLB debutJuly 2, 1885, for the Detroit WolverinesLast MLB appearanceSeptember 10, 1906, for the Detroit Tigers...

Borough in Morris County, New Jersey, US Borough in New JerseyFlorham Park, New JerseyBorough200-year-old oak tree at Brooklake Country Club SealLocation of Florham Park in Morris County highlighted in red (right). Inset map: Location of Morris County in New Jersey highlighted in orange (left).Census Bureau map of Florham Park, New JerseyFlorham ParkLocation in Morris CountyShow map of Morris County, New JerseyFlorham ParkLocation in New JerseyShow map of New JerseyFlorham ParkLocation in the...

American Basketball Association 1970-1971Dettagli della competizioneSport Pallacanestro OrganizzatoreABA Periodo14 ottobre 1970 —18 maggio 1971 Squadre11 (in 2 gironi) VerdettiTitolo East Kentucky Colonels Titolo West Utah Stars Campione Utah Stars(1º titolo) MVPMel Daniels Miglior allenatoreAl Bianchi Miglior marcatoreDan Issel MVP delle finaliZelmo Beaty Cronologia della competizioneed. successiva → ← ed. precedente Modifica dati s...

提示:此条目页的主题不是中華人民共和國最高領導人。 中华人民共和国 中华人民共和国政府与政治系列条目 执政党 中国共产党 党章、党旗党徽 主要负责人、领导核心 领导集体、民主集中制 意识形态、组织 以习近平同志为核心的党中央 两个维护、两个确立 全国代表大会 (二十大) 中央委员会 (二十届) 总书记:习近平 中央政治局 常务委员会 中央书记处 �...

Sprinters Stakes Arrivée de l'édition 2022 Groupe 1Données clés Localisation Hippodrome de Nakayama Inaugurée 1967 Site web japanracing.jp - Centaur Stakes & Sprinters Stakes Informations sur la course Longueur 1 200 mètres Piste Gazon, corde à droite Qualification Chevaux de 3 ans et plus Poids 3 ans 55 kg / 4 ans et plus 57 kgdécharge : 2 kg pour les femelles2 kg les 3 ans nés dans l'hémisphère sud Gains 214 800 000 ¥ Record 1'0670 (Lord Kanalo...

American ballerina (1926–2021) Marjorie TallchiefTallchief in 1956BornMarjorie Louise Tall Chief(1926-10-19)October 19, 1926Denver, Colorado, U.S.DiedNovember 30, 2021(2021-11-30) (aged 95)Boca Raton, Florida, U.S.OccupationBallerinaSpouse George Skibine (m. 1947; died 1981)Children2CareerFormer groupsParis Opera Ballet Marjorie Tallchief (born Marjorie Louise Tall Chief; October 19, 1926 – November 30, 2021) was a...

Pseudoreligious belief Not to be confused with Israelis in the United Kingdom, British Jews, or Christian Zionism in the United Kingdom. Israel in Britain, an 1890 book advocating British Israelism. According to the doctrine, the Ten Lost tribes of Israel found their way to Western Europe and Britain, becoming the ancestors of the British, the English and related peoples. British Israelism (also called Anglo-Israelism) is the British nationalist, pseudoarchaeological, pseudohistorical[1&#...

Czech tennis player (born 1996) Karolína MuchováMuchová at the 2023 US OpenCountry (sports) Czech RepublicBorn (1996-08-21) 21 August 1996 (age 27)Olomouc, Czech RepublicHeight1.80 m (5 ft 11 in)Turned pro2013PlaysRight (two-handed backhand)CoachEmil Miške (2017–2019, Apr 2023–)[1]Kirsten Flipkens (2023)[2]Prize moneyUS$ 6,509,545SinglesCareer record279–137 (67.1%)Career titles1Highest rankingNo. 8 (11 September 2023)...

Fictional character Dave MalucciErik Palladino as Dave MalucciFirst appearanceOctober 7, 1999(6x02, Last Rites)Last appearanceOctober 25, 2001(8x04, Never Say Never)Portrayed byErik PalladinoDuration1999–2001In-universe informationNicknameDr. DaveGenderMaleTitleResident (1999-2001)OccupationPhysicianChildrenUnnamed Child[1]Born1972[2] Dr. Dave Malucci is a fictional character on the NBC prime time drama ER. He was portrayed by Erik Palladino. Season 6 Dave Malucci first appe...

This article is about the village of Keadue in County Roscommon. For the townland in County Donegal, see Keadue, County Donegal. Village in Connacht, IrelandKeadue / Keadew Irish: CéideadhVillageKeadue's main streetKeadue / KeadewLocation in IrelandCoordinates: 54°04′05″N 8°11′58″W / 54.0681°N 8.1994°W / 54.0681; -8.1994CountryIrelandProvinceConnachtCountyCounty RoscommonElevation82 m (269 ft)Population (2016)[1]154Time zoneUTC+0 (WE...

Casa di Arthur Shores danneggiata da un attentato dinamitardo il 4 settembre 1963 (foto scattata il giorno successivo). Bombingham fu il soprannome che venne dato alla città di Birmingham, in Alabama, negli anni '50 e '60 a causa dei numerosi attentati accadutivi per mano del Ku Klux Klan.[1] Indice 1 Descrizione 1.1 Antefatti 1.2 Storia 1.2.1 Il culmine del 1963 1.3 Risultati 2 Note 3 Voci correlate Descrizione Antefatti Giunti agli anni '40, la comunità nera stava cercando di tras...

Pour les articles homonymes, voir Marie Mancini (homonymie). Maria ManciniBiographieNaissance 1355PiseDécès 22 janvier 1431PiseActivité Religieuse chrétienneAutres informationsOrdre religieux Ordre des PrêcheursÉtape de canonisation BienheureuseFête 30 janviermodifier - modifier le code - modifier Wikidata La Bienheureuse Marie Catherine Mancini, née en 1355 à Pise et morte dans la même ville le 22 janvier 1431, est une religieuse dominicaine italienne. Le Pape Pie IX confirme son ...

Teaching that Mary was conceived free from original sin This article is about the doctrine that Mary was conceived free from original sin. For the conception of Jesus, see Virgin birth of Jesus. For other uses, see Immaculate Conception (disambiguation). Several terms redirect here. For other uses, see Immacolata (disambiguation), Immaculata (disambiguation), Immaculate (disambiguation), and Mary Immaculate (disambiguation). Our Lady of the Immaculate ConceptionThe Immacul...

この項目では、本間洋平作の小説と、それを原作とした映画について説明しています。その他の用法については「家族ゲーム (曖昧さ回避)」をご覧ください。 『家族ゲーム』(かぞくゲーム)は、本間洋平作の日本の小説。1981年の第5回すばる文学賞を受賞した。またそれを原作とした映画、およびテレビドラマ。 1982年、テレビ朝日でこの小説を原作とする2時間ドラ�...





![{\displaystyle \operatorname {ECM} ({\hat {\theta }})=\operatorname {E} {\big [}({\hat {\theta }}-\theta )^{2}{\big ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ddc9b0b92f04927813433c3a685a5addb8a24bd)

![{\displaystyle {\begin{aligned}\operatorname {ECM} ({\hat {\theta }})\equiv \mathbb {E} (({\hat {\theta }}-\theta )^{2})&=\mathbb {E} \left[\left({\hat {\theta }}-\mathbb {E} ({\hat {\theta }})+\mathbb {E} ({\hat {\theta }})-\theta \right)^{2}\right]\\&=\mathbb {E} \left[\left({\hat {\theta }}-\mathbb {E} ({\hat {\theta }})\right)^{2}+2\left(({\hat {\theta }}-\mathbb {E} ({\hat {\theta }}))(\mathbb {E} ({\hat {\theta }})-\theta )\right)+\left(\mathbb {E} ({\hat {\theta }})-\theta \right)^{2}\right]\\&=\mathbb {E} \left[\left({\hat {\theta }}-\mathbb {E} ({\hat {\theta }})\right)^{2}\right]+2\mathbb {E} \left[({\hat {\theta }}-\mathbb {E} ({\hat {\theta }}))(\mathbb {E} ({\hat {\theta }})-\theta )\right]+\mathbb {E} \left[\left(\mathbb {E} ({\hat {\theta }})-\theta \right)^{2}\right]\\&=\mathbb {E} \left[\left({\hat {\theta }}-\mathbb {E} ({\hat {\theta }})\right)^{2}\right]+2(\mathbb {E} ({\hat {\theta }})-\theta )\overbrace {\mathbb {E} ({\hat {\theta }}-\mathbb {E} ({\hat {\theta }}))} ^{=\mathbb {E} ({\hat {\theta }})-\mathbb {E} ({\hat {\theta }})=0}+\mathbb {E} \left[\left(\mathbb {E} ({\hat {\theta }})-\theta \right)^{2}\right]\\&=\mathbb {E} \left[\left({\hat {\theta }}-\mathbb {E} ({\hat {\theta }})\right)^{2}\right]+\mathbb {E} \left[\left(\mathbb {E} ({\hat {\theta }})-\theta \right)^{2}\right]\\&=\operatorname {Var} ({\hat {\theta }})+\operatorname {sesgo} ({\hat {\theta }},\theta )^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b139fc31d3d86a8d1ea6195d405e87682699dda7)










![{\displaystyle {\begin{aligned}\operatorname {ECM} (S_{a}^{2})&=\operatorname {E} \left(\left({\frac {n-1}{a}}S_{n-1}^{2}-\sigma ^{2}\right)^{2}\right)\\&={\frac {n-1}{na^{2}}}[(n-1)\gamma _{2}+n^{2}+n]\sigma ^{4}-{\frac {2(n-1)}{a}}\sigma ^{4}+\sigma ^{4}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ce6e828b16c7a44e02db5c934a8a1d0ed9a37c1)

















