Ensayo sobre el principio de la población
| |||||||||||||||||||||||||
Read other articles:

Scott W. Hahn (lahir 28 Oktober 1957) adalah seorang apologet Kristen, profesor, penulis kontemporer, dan teolog awam[1] Katolik dari Amerika Serikat. Hahn pernah melayani sebagai seorang pendeta Presbiterian dan kemudian berpindah keyakinan ke iman Katolik. Karya-karya tulis Hahn yang populer misalnya Rome Sweet Home dan The Lamb's Supper: The Mass as Heaven on Earth. Pengajaran-pengajarannya dimuat dalam sejumlah distribusi audio melalui Lighthouse Catholic Media. Hahn dikenal kare...

Firefly IATA ICAO Kode panggil FY FFM FIREFLY Didirikan2007PenghubungBandar Udara Sultan Abdul Aziz ShahPenghubung sekunderBandar Udara Internasional PenangAliansiMalaysia AirlinesArmada12Tujuan23SloganYour Community Airline(Maskapai Komunitas Anda)Kantor pusatGeorge Town, Penang, MalaysiaTokoh utamaDatuk Eddy LeongSitus webhttp://www.fireflyz.com.my/ FlyFirefly Sdn Bhd, beroperasi sebagai Firefly, adalah anak perusahaan maskapai penerbangan Malaysia Airlines yang didirikan pada tanggal 3 Apr...

Asosiasi Sepak Bola ParaguayCONMEBOLDidirikan1906Kantor pusatLuqueBergabung dengan FIFA1925Bergabung dengan CONMEBOL1921PresidenJuan Angel NapoutWebsitewww.apf.org.py Asosiasi Sepak Bola Paraguay (Spanyol: Asociación Paraguaya de Futbol (APF)code: es is deprecated adalah badan pengendali sepak bola di Paraguay. Kompetisi Badan ini menyelenggarakan beberapa kompetisi di Paraguay, yakni: Divisi Utama Paraguay Divisi Dua Liga Paraguay Divisi Tiga Liga Paraguay Tim nasional Badan ini juga merupa...

العلاقات البحرينية السلوفينية البحرين سلوفينيا البحرين سلوفينيا تعديل مصدري - تعديل العلاقات البحرينية السلوفينية هي العلاقات الثنائية التي تجمع بين البحرين وسلوفينيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: �...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Indian association football club based in Goa Football clubSalgaocarFull nameSalgaocar Football ClubShort nameSFCFounded1956; 68 years ago (1956) (as Vimson Club)1961; 63 years ago (1961) (as Salgaocar Sports Club)GroundDuler StadiumCapacity10,000OwnerShivanand Salgaocar (V. M. Salgaocar Group of Companies)WebsiteClub website Home colours Away colours Salgaocar Football Club (formerly Salgaocar Sporting Club) is an Indian professional football club based in...

French administrator and politician Joseph Pelet de la LozèrePelet de la Lozère, Auditor (1806) by his fellow-auditor Frédéric-Christophe d'HoudetotBornPrivat Joseph Claramont, comte Pelet de la Lozère(1785-07-12)12 July 1785Saint-Jean-du-Gard, Gard, FranceDied9 February 1871(1871-02-09) (aged 85)Villers-Cotterêts, Aisne, FranceNationalityFrenchOccupation(s)Lawyer, politician Privat Joseph Claramont, comte Pelet de la Lozère (12 July 1785 – 9 February 1871) was a French administ...

ヨハネス12世 第130代 ローマ教皇 教皇就任 955年12月16日教皇離任 964年5月14日先代 アガペトゥス2世次代 レオ8世個人情報出生 937年スポレート公国(中部イタリア)スポレート死去 964年5月14日 教皇領、ローマ原国籍 スポレート公国親 父アルベリーコ2世(スポレート公)、母アルダその他のヨハネステンプレートを表示 ヨハネス12世(Ioannes XII、937年 - 964年5月14日)は、ロ...

ملوك شبه جزيرةإيبيريا الأندلس (بني أمية · الطوائف) أراغون أستورياس قشتالة كاتالونيا جليقية غرناطة ليون مايوركا نافارا البرتغال إسبانيا (العصور الوسطى · الحديث) سويبي بلنسية بقيرة القوط الغربيين فُتحت الأندلس عام (92 هـ/710م) في عهد الخليفة الأموي الوليد بن عب�...

Anti-Semitism in the 21st century redirects here. For the documentary film, see Anti-Semitism in the 21st Century: The Resurgence. Part of a series onAntisemitism Part of Jewish history and discrimination History Timeline Reference Definitions IHRA definition Jerusalem Declaration Nexus Document Three Ds Geography Argentina Australia Austria Belarus Belgium Canada Chinese Chilean Costa Rican Europe France Dreyfus affair 21st century 21st-century Germany Greece Hungary 21st-century Italy Japa...

American judge (born 1960) Rowan WilsonWilson in 2023Chief Judge of the New York Court of AppealsIncumbentAssumed office April 18, 2023Appointed byKathy HochulPreceded byAnthony Cannataro (acting)Associate Judge of the New York Court of AppealsIn officeFebruary 6, 2017 – April 18, 2023Appointed byAndrew CuomoPreceded byEugene F. Pigott Jr.Succeeded byCaitlin Halligan Personal detailsBorn (1960-09-03) September 3, 1960 (age 63)Pomona, California, U.S.Political partyDemocrat...

Katedral ErfurtGereja Katedral Santa Maria di Erfurt Erfurter Dom Hohe Domkirche St. Marien zu Erfurt Propsteikirche Beatae Mariae Virginis Katedral Erfurt50°58′33″N 11°01′24″E / 50.9759°N 11.0233°E / 50.9759; 11.0233Koordinat: 50°58′33″N 11°01′24″E / 50.9759°N 11.0233°E / 50.9759; 11.0233LokasiErfurt, ThuringiaNegaraJermanDenominasiGereja Katolik RomaSitus webwww.dom-erfurt.deSejarahDedikasiSanta Perawan MariaArsite...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2016) مومباي، عاصمة الهند بلد التناقضات والحضارات القديمة ومبتغى سفن واكتشافات القرون الوسطى، قرون من التاريخ الطويل، تتوفر على العديد من المواقع ذات أهمية تاري�...

Bacary Sagna Sagna pada tahun 2012Informasi pribadiNama lengkap Bacary SagnaTanggal lahir 14 Februari 1983 (umur 41)Tempat lahir Sens, PrancisTinggi 1,76 m (5 ft 9+1⁄2 in)[1]Posisi bermain Bek kananKarier junior1992–1997 Sens1997–2002 AuxerreKarier senior*Tahun Tim Tampil (Gol)2002–2004 Auxerre B 37 (3)2004–2007 Auxerre 87 (0)2007–2014 Arsenal 213 (4)2014–2018 Manchester City 54 (0)2018 Benevento 13 (1)2018–2019 Montreal Impact 35 (2)Total 439 ...

Charlie Chan Warner Oland dans le rôle de Charlie Chandans Charlie Chan's Secret Origine Américain d'origine chinoise Activité Détective Créé par Earl Derr Biggers Interprété par Warner OlandSidney TolerRoland WintersPeter Ustinov Première apparition La Maison sans clef (1925) Dernière apparition Le Gardien des clés (1932) modifier Charlie Chan, est un personnage de fiction créé en 1925 par Earl Derr Biggers, c'est un détective américain d'origine chinoise . Il est le h�...

Pour les articles homonymes, voir Carrel. Alexis CarrelFonctionRégentFondation française pour l'étude des problèmes humains1941-1944BiographieNaissance 28 juin 1873Sainte-Foy-lès-LyonDécès 5 novembre 1944 (à 71 ans)ParisNom de naissance Marie-Joseph-Auguste Carrel-BillardNationalité françaiseFormation Université de Lyon (docteur en médecine) (1900)Lycée Saint-MarcActivités Biologiste, physiologiste, chirurgien, sociologuePère Alexis Carrel-Billiard (d)Conjoint Anne Gourle...
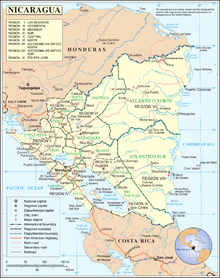
Overview of and topical guide to Nicaragua See also: Index of Nicaragua-related articles The Flag of NicaraguaThe Coat of arms of Nicaragua The location of Nicaragua An enlargeable map of the Republic of Nicaragua The following outline is provided as an overview of and topical guide to Nicaragua: Nicaragua – sovereign, representative democratic republic and the most extensive nation in Central America.[1] It is also the least densely populated with a demographic similar in size ...
بوكس إلدر الإحداثيات 44°06′55″N 103°04′55″W / 44.115277777778°N 103.08194444444°W / 44.115277777778; -103.08194444444 [1] تاريخ التأسيس 1907 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة بنينغتون خصائص جغرافية المساحة 36.353898 كيلومتر مربع36.040743 كيلومت...

Pour les articles homonymes, voir Les Patriotes et LP. Les Patriotes Logotype officiel. Présentation Président Florian Philippot Fondation 16 mai 2017 (association)29 septembre 2017(parti) Scission de Front national Scission dans La Gauche patriote (2019) Siège 122, rue des Rosiers93400 Saint-Ouen-sur-Seine Slogan « Le meilleur pour la France » Positionnement Extrême droite[1],[2],[3] Idéologie Souverainisme[1]Gaullisme[1]Europhobie[4],[5]Républicanisme[1]Populisme[6]Conspi...

Polytech Lyon (ex-ISTIL)HistoireFondation Septembre 1992StatutType École d'ingénieursNom officiel École Polytechnique Universitaire de l'université Lyon 1Fondateur Gérard Fontaine et Paul BéthouxDirecteur Emmanuel PerrinMembre de Réseau Polytech, Conférence des grandes écoles, université Claude-Bernard-Lyon-ISite web polytech.univ-lyon1.frChiffres-clésÉtudiants 700 en cycle ingénieur (2019)LocalisationPays FranceCampus La Doua / Technopole DiderotVille Villeurbanne RoanneLocalisa...




