Engranaje planetario
|
Read other articles:

Untuk kegunaan lain, lihat Bremen. Bremen, AlabamakotaNegaraAmerika SerikatNegara bagianAlabamacountyCullmanZona waktuUTC-6 (Central (CST)) • Musim panas (DST)UTC-5 (CDT)Kode pos35033Kode area telepon256 Bremen merupakan sebuah kota di county Cullman, Alabama, Amerika Serikat. Kota tak berhubungan ini memiliki penduduk 8.198 pada tahun 2000 (termasuk sebagian penduduk Colony, Dodge City, dan Good Hope). Luasnya sekitar 88.9 km². Kode pos daerah ini adalah 35033. Jalan raya u...

Vivian SilverLahir(1949-02-02)2 Februari 1949Winnipeg, Manitoba, KanadaMeninggal7 Oktober 2023 (usia 74)Be'eri, IsraelSebab meninggalPembantaian Be'eriTempat kerjaInstitut Strategi Perdamaian dan Pembangunan Negev (1998–2014)OrganisasiWomen Wage PeaceDikenal atasAktivisme perdamaianAnak2 Vivian Silver (Ibrani: ויויאן סילברcode: he is deprecated ) (2 Februari 1949 – 7 Oktober 2023) adalah seorang pegiat perdamaian dan hak-hak perempuan Kanada-Israel.[1 ...

Evan SpiegelLahirEvan Thomas Spiegel[1]04 Juni 1990 (umur 33)[2]Los Angeles, California, Amerika SerikatPendidikanUniversitas StanfordPekerjaanCEO (industri teknologi)Dikenal atasPendiri SnapchatKekayaan bersih US$1,5 miliar (September 2014)[3] Evan Thomas Spiegel (lahir 4 Juni 1990) adalah pengusaha Amerika Serikat yang menjadi pendiri dan CEO aplikasi perangkat bergerak Snapchat. Kehidupan awal dan pendidikan Evan lahir di Los Angeles, California, dari pas...

كأس ألبانيا 1998–99 تفاصيل الموسم كأس ألبانيا النسخة 47 البلد ألبانيا التاريخ بداية:أغسطس 1998 نهاية:22 مايو 1999 المنظم اتحاد ألبانيا لكرة القدم البطل نادي تيرانا كأس ألبانيا 1997–98 كأس ألبانيا 1999–2000 تعديل مصدري - تعديل كأس ألبانيا 1998–99 (بالألبان�...

French archer Léonce Quentin Olympic medal record Men's Archery 1920 Antwerp moving bird 28 m 1920 Antwerp Team Competition 33 m 1920 Antwerp Team Competition 50 m 1920 Antwerp Team Competition 28 m Léonce Gaston Quentin (16 February 1880 – 1 December 1957) was a French archer who competed in the 1920 Summer Olympics. In 1920 he won four Olympic medals, one silver in the individual moving bird 28 metres event and two silver and one bronze in team competitions.[1] References ^ ...

PPI beralih ke halaman ini. Untuk kegunaan lain, lihat PPI (disambiguasi). Partai Pemuda Indonesia Ketua umumHoras SihombingSekretaris JenderalSyarir TamberoKantor pusatKasablanka, Jakarta SelatanIdeologiPancasila dan UUD 45 dan Partai TerbukaSitus webhttp://www.partaipemudaindonesia.com/Politik IndonesiaPartai politikPemilihan umum Partai Pemuda Indonesia (PPI) adalah sebuah partai politik di Indonesia yang didirikan pada tanggal 5 Maret 2007, oleh sekelompok aktivis dari Komite Nasional Pem...

1976 video game 1976 video gameF-1Japanese promotional sales flyerDeveloper(s)Nakamura Manufacturing Company (Namco)Publisher(s)JP: Nakamura Manufacturing CompanyNA: Atari, Inc.Designer(s)Sho OsugiPlatform(s)ArcadeReleaseJP: October 1976NA: November 1976Genre(s)RacingMode(s)Single-player F-1 is a 1976 electro-mechanical arcade racing game developed and published by Nakamura Manufacturing Company (Namco), and distributed in North America by Atari, Inc. The player uses a steering wheel to contr...

В Википедии есть статьи о других людях с именем Соломон. У этого термина существуют и другие значения, см. Соломон (значения). Соломон IIгруз. სოლომონ II Соломон II, царь Имеретии Царь Имеретии 1789 — 20 февраля 1810 Предшественник Давид II Преемник титул упразднёнАлександр I...

Fusillade du 11 novembre 1984 à Châteaubriant Cible Travailleurs immigrés Coordonnées 47° 43′ 11″ nord, 1° 22′ 39″ ouest Date 11 novembre 1984 Type Fusillade de masse Armes Fusil à pompe Remington Morts 2 Blessés 5 Auteurs Frédéric Boulay Mouvance Xénophobie Géolocalisation sur la carte : France Géolocalisation sur la carte : Pays de la Loire Géolocalisation sur la carte : Loire-Atlantique modifier La fusillade du 11 no...

This article is about the Chinese version. For the North American version produced from 1986 to 2019, see Ford Taurus. Motor vehicle Ford Taurus (China)Ford Taurus VII faceliftOverviewManufacturerChangan FordProduction2015–2022Model years2016–2022AssemblyHangzhou, Zhejiang, China (Changan Ford Hangzhou Plant)DesignerBogusław Paruch, Berk Keskin, Andrea di Buduo, Dillon Blanski, Ernesto Rupar[1]Body and chassisClassFull-size carBody style4 door sedanLayoutFront-engine, f...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau denga...

Brendan IribeIribe memegang sebuah Oculus Rift pada 2015Lahir12 Agustus 1979 (umur 44)Maryland, Amerika SerikatAlmamaterUniversity of Maryland, College Park (keluar)PekerjaanVP pada divisi Oculus dari Facebook (dulu)Dikenal atasSalah satu pendiri dan CEO Oculus VR, Inc.Situs webbrendaniribe.com Brendan Trexler Iribe (/ˈiːriːb/; lahir 12 Agustus 1979) adalah seorang programmer permainan, wirausahawan dan CEO awal dan salah satu pendiri Oculus VR, Inc. dan Scaleform. Ia menjadi mitra m...
本文或本章節是關於未來的公共运输建設或計划。未有可靠来源的臆測內容可能會被移除,現時內容可能與竣工情況有所出入。 此条目讲述中国大陆處於施工或详细规划阶段的工程。设计阶段的資訊,或許与竣工后情況有所出入。无可靠来源供查证的猜测会被移除。 设想中的三条路线方案[1]。 臺灣海峽隧道或臺湾海峡橋隧(英語:Taiwan Strait Tunnel Project)是一项工程�...

Skyline of Dallas (use cursor to identify buildings) Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) Dallas, the third-largest city in the U.S. state of Texas, is the site of 42 completed high-rise buildings over 350 feet (107 m), 20 of which stand taller than 492 feet (150 m).[1][2][3] The tallest building in the city is the Bank of America Plaza, which rises 92...

Pour les articles homonymes, voir ADR. ADR Données clés Présentation Titre (fr) Accord relatif au transport international des marchandises dangereuses par route(en) Agreement concerning the International Carriage of Dangerous Goods by Road Abréviation ADR Organisation internationale Commission économique pour l’Europe des Nations unies Pays Nations unies Territoire d'application 54 pays Langue(s) officielle(s) Anglais, français Type Traité Branche Droit du transport Adoption et entr...
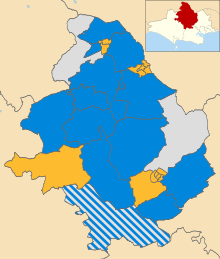
Local election in Dorset Map of North Dorset showing the results of the 2007 local election. Elections to North Dorset District Council were held on 3 May 2007, alongside other local elections across the United Kingdom. All 33 seats were up for election. The Conservative Party gained the council from no overall control. Results Results[1] Party Seats before Seats after Change Conservative Party 15 17 2 Liberal Democrats 13 13 Other 5 3 2 References ^ BBC NEWS | Election 2007 | Local C...

Resolusi 882Dewan Keamanan PBBBendera MozambikTanggal5 November 1993Sidang no.3.305KodeS/RES/882 (Dokumen)TopikSituasi di MozambikRingkasan hasil15 mendukungTidak ada menentangTidak ada abstainHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Rusia Britania Raya Amerika SerikatAnggota tidak tetap Brasil Tanjung Verde Djibouti Spanyol Hungaria Jepang Maroko Selandia Baru Pakistan Venezuela Re...

Questa voce sull'argomento calciatori olandesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Brandley KuwasNazionalità Paesi Bassi Curaçao Altezza178 cm Peso70 kg Calcio RuoloAttaccante Squadra svincolato CarrieraGiovanili Hellas Sport AZ Alkmaar Kooger Squadre di club1 2012-2015 Volendam103 (15)[1]2015-2016 Excelsior34 (4)2016-2019 Heracles Almelo92...

For other uses, see Aeson (disambiguation). King of Iolcus AesonKing of IolcusMedea rejuvenates Aeson by Nicolas-André MonsiauReigncirca 15th century BCSuccessorPeliasBornunknownSpousePolymele or PolymedeIssueJason and PromachusFatherCretheusMotherTyro In Greek mythology, Aeson (/ˈiːsɒn/;[1] Ancient Greek: Αἴσων Aísōn) was a king of Iolcus in Thessaly. He was the father of the hero Jason. According to one version of the story, he was imprisoned by his half-brother Pelias, ...





