Ecuación de Arrhenius
|
Read other articles:

Helen MorganHelen Morgan, 1935LahirHelen Riggins(1900-08-02)2 Agustus 1900Danville, Illinois, Amerika SerikatMeninggal9 Oktober 1941(1941-10-09) (umur 41)Chicago, Illinois, Amerika SerikatPekerjaanPenyanyi, pemeranSuami/istriMaurice Maschke, Jr. (m. 1933; bercerai 1935) Lloyd Johnston (m. 1941; kematian Morgan 1941) Helen Morgan (2 Agustus 1900 – 9 Oktober 1941)[1&...

Ayam hutan merah Status konservasi Risiko Rendah Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Galliformes Famili: Phasianidae Genus: Gallus Spesies: G. gallus Nama binomial Gallus gallus(Linnaeus, 1758) Telur ayam hutan merah Ayam hutan merah atau dalam nama ilmiahnya Gallus gallus adalah sejenis burung berukuran sedang, dengan panjang sekitar 78 cm, dari suku Phasianidae. Ayam betina berukuran lebih kecil, dengan panjang sekitar 46 cm. Ayam hutan ja...

Robert T. HenryLahir(1923-11-27)27 November 1923Greenville, MississippiMeninggal3 Desember 1944(1944-12-03) (umur 21)Luchem, JermanTempat pemakamanGreenville Cemetery Greenville, MississippiPengabdianAmerika SerikatDinas/cabangAngkatan Darat Amerika SerikatLama dinas1943–1944PangkatPrivatKesatuanResimen Infanteri ke-16, Divisi Infanteri ke-1Perang/pertempuranPerang Dunia IIPenghargaanMedal of Honor Robert T. Henry (27 November 1923 – 3 Desember 1944) adalah seorang...

Italian footballer Sebastiano Luperto Luperto with Napoli in 2019Personal informationDate of birth (1996-09-06) 6 September 1996 (age 27)Place of birth Lecce, ItalyHeight 1.91 m (6 ft 3 in)[1]Position(s) Centre-backTeam informationCurrent team EmpoliNumber 33Youth career Lecce0000–2015 NapoliSenior career*Years Team Apps (Gls)2015–2023 Napoli 22 (0)2016–2017 → Pro Vercelli (loan) 32 (0)2017–2018 → Empoli (loan) 28 (2)2020–2021 → Crotone (loan) 23 (0...

Village in Massachusetts, United StatesMagnoliaVillageAerial view of Magnolia village in 2016MagnoliaCoordinates: 42°34′30″N 70°42′45″W / 42.57500°N 70.71250°W / 42.57500; -70.71250CountryUnited StatesStateMassachusettsCountyGloucester, MassachusettsTime zoneUTC-5 (Eastern)Zip Code01930 Magnolia is a small village in Gloucester, Massachusetts, located on the Manchester-by-the-Sea, Massachusetts town line in the southwestern part of the city. Straddling the...

Video game for the Nintendo 3DS This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Gaist Crusher – news · newspapers · books · scholar · JSTOR (March 2021) (Learn how and when to remove this template message) Gaist CrusherCover artwork of the video gameガイストクラッシャー(Gaisutokurasshā)GenreAction...

Voce principale: Brescia Calcio. Brescia CalcioStagione 2008-2009Sport calcio Squadra Brescia Allenatore Serse Cosmi (1ª-5ª), poi Nedo Sonetti (6ª-40ª), poi Alberto Cavasin (41ª-42ª e play-off) Presidente Luigi Corioni Serie B4º posto PlayoffFinale Coppa ItaliaTerzo turno Maggiori presenzeCampionato: Viviano e Zambrella (37) Miglior marcatoreCampionato: Caracciolo (15) StadioStadio Mario Rigamonti Maggior numero di spettatori5 500 vs Ascoli (20 settembre 2008) Minor numero d...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Cycling race 2012 Tour of the Basque Country2012 UCI World Tour, race 9 of 28Race detailsDates2–7 AprilStages6Distance824.6 km (512.4 mi)Winning time20h 58' 15Results Winner Samuel Sánchez (Spain) (Euskaltel–Euskadi) Second Joaquim Rodríguez (Spain) (Team Katusha) Third Bauke Mollema (Netherlands) (Rabobank) Points Samuel Sánchez (Spain) (Euskaltel–Euskadi) Mountains Mads Christensen (Denmark) (Team Saxo Ban...

Chronologies Données clés 1904 1905 1906 1907 1908 1909 1910Décennies :1870 1880 1890 1900 1910 1920 1930Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocratique du Congo, Côte d'Ivoire, Djibouti, Égyp...
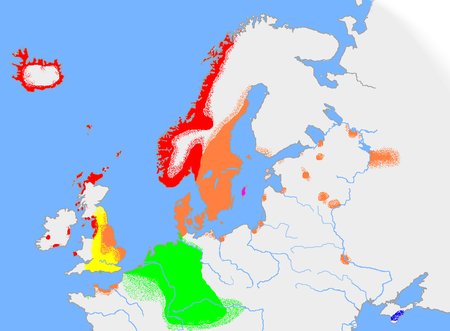
NorskaNorskTalas i NorgeRegionNordenAntal talare4,3 miljoner[1]StatusstabiltSpråkfamiljIndoeuropeiska språkGermanska språkNordgermanska språkVäst/Östnordiska språkNorskaSkriftsystemLatinska alfabetetOfficiell statusOfficiellt språk i Norge Nordiska rådetSpråkmyndighetNorsk språkrådSpråkkoderISO 639‐1no, nb, nnISO 639‐2nor, nob, nnoISO 639‐3nor – inkluderande kodIndividuella koder:nob – Bokmålnno – Nynorska Norska (norska: norsk) är...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Slovenská informačná služba – news · newspapers · books · scholar · JSTOR (January 2013) (Learn how and when to remove this message) Slovak Information ServiceSlovenská informačná služba(SIS)Seal of the Slovak Information ServiceAgency overviewFormed15 ...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (juillet 2015). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? ...

Fritz SchaperNaissance 31 juillet 1841AlslebenDécès 29 novembre 1919 (à 78 ans)BerlinSépulture Cimetière de Jérusalem et de la nouvelle église (division IV)Période d'activité 1860-1900Nom de naissance Hugo Wilhelm Friedrich SchaperNationalité allemandeActivités Sculpteur, professeur d'universitéFormation Académie prussienne des Arts (en)Enfants Wolfgang Schaper (en)Eva Schaper (d)Distinction Ordre Pour le Mérite pour les sciences et arts (d)Vue de la sépulture.modifier - m...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1976 United States presidential election in Maine – news · newspapers · books · scholar · JSTOR (January 2017) (Learn how and when to remove this message) Main article: 1976 United States presidential election 1976 United States presidential election in Maine ...

Canadian federal agency in charge of elections and referendums For information on elections in Canada, see Elections in Canada. Elections CanadaÉlections CanadaAgency overviewFormedJuly 1, 1920 (1920-07-01)[1]JurisdictionCanadaHeadquarters30 Victoria Street Gatineau, Quebec K1A 0M6Employees500 (Permanent) up to 235,000 (election period)[2]Annual budget$628,864,260 (2021–22)[3]Agency executiveStéphane Perrault, Chief Electoral Officer of CanadaWebsite...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

يعني السمو (من sublīmis باللغة اللاتينية) في علم الجماليات صفة العظمة، سواء كانت جسدية أو أخلاقية أو فكرية أو ميتافيزيقية أو جمالية أو روحانية أو فنية.[1][2][3] ويشير هذا المصطلح بالأخص إلى العظمة التي تتجاوز كل الاحتمالات التي يمكن عدها أو قياسها أو محاكاتها. الفلسف�...

凡例北条泰時 和田合戰義秀惣門押破(歌川国芳)時代 平安時代末期 - 鎌倉時代前期生誕 寿永2年(1183年)死没 仁治3年6月15日(1242年7月14日)改名 金剛(幼名)→江間大(太)郎頼時(初名)→泰時、観阿(法名)墓所 神奈川県鎌倉市大船 常楽寺官位 駿河守、武蔵守、讃岐守、左京権大夫、正四位下幕府 鎌倉幕府侍所別当、六波羅探題北方、3代執権(1224年 - 1242年�...

Jewish religious schooling program Talmud Torah in Mea She'arim Talmud Torah in Samarkand A teacher and a student in a Talmud Torah, Bnei Brak, 1965 Talmud Torah (Hebrew: תלמוד תורה, lit. 'Study of the Torah') schools were created in the Jewish world, both Ashkenazic and Sephardic, as a form of religious school for boys of modest backgrounds, where they were given an elementary education in Hebrew, the scriptures (especially the Torah), and the Talmud (and halakha). This was meant to...


























