Distribución gamma
| ||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Coalition government in Great Britain 1783 Fox–North coalitionApril–December 1783 Fox (left) and North (right)Date formed2 April 1783 (1783-04-02)Date dissolved18 December 1783 (1783-12-18)People and organisationsMonarchGeorge IIIPrime MinisterDuke of PortlandSecretaries of StateCharles James FoxLord NorthTotal no. of members15 appointmentsMember partiesFoxitesNorthitesStatus in legislatureMajority (coalition)Opposition partyPittitesOpposition leadersWilliam ...

Kunio NakagawaNama asli中川 州男Lahir(1898-01-23)23 Januari 1898Meninggal24 November 1944(1944-11-24) (umur 46)Pulau Peleliu, PalauPengabdian JepangDinas/cabang Angkatan Darat Kekaisaran JepangLama dinas1918–1944PangkatLetnan jenderal (anumerta)Perang/pertempuranPerang Tiongkok-Jepang Kedua Insiden Jembatan Marco Polo Perang Dunia II Pertempuran Peleliu Kunio Nakagawa (中川 州男code: ja is deprecated , Nakagawa Kunio, 23 Januari 1898 – 24 November...

Masjid Perempuan Xiaotaoyuan di Shanghai, Tiongkok. Sebuah masjid khusus perempuan di Byblos, Lebanon. Masjid perempuan (Hanzi: [清真]女寺; Pinyin: [Qīngzhēn] nǚ sì) telah ada di Tiongkok selama beberapa ratus tahun.[1] Masjid ini dapat ditemukan di provinsi-provinsi Tiongkok seperti Henan, Shanxi dan Hebei.[2] Beberapa negara di luar Tiongkok juga memiliki masjid khusus perempuan, tetapi jarang. Di Indonesia, masjid perempuan salah satunya terdapat di Padang P...

2005 album by Purple Ribbon All-Stars Big Boi Presents... Got Purp? Vol. IIStudio album by Purple Ribbon All-StarsReleasedNovember 22, 2005 (2005-11-22)Recorded2005GenreSouthern hip hopLength1:12:03LabelPurple RibbonVirginProducerB-DonCarl MoCharles K.C. SandersC.K.P.Janelle MonáeMr. DJNate Rocket WonderOrganized NoizeSwiffmanThe Beat BulliesThe Booom BoizePurple Ribbon All-Stars chronology Got That Purp(2005) Big Boi Presents... Got Purp? Vol. II(2005) Singles from Big Bo...
جزء من سلسلة مقالات حولتاريخ إندونيسيا ما قبل التاريخإنسان جاوة1,000,000 ق.ح إنسان فلوريس94,000 - 12,000 ق.ح نظرية كارثة توبا 75000 ق.ح ثقافة بوني 400 ق.م الممالك الهندوسية البوذيةكوتاي القرن الرابع تاروماناجارا358–669 كالنجاالقرن ال6– القرن ال7 مالايوالقرن ال6 سريفيجاياالقرن ال7– القرن ا...

Paranthropus robustusRentang fosil: Pliocene-Pleistocene Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mammalia Ordo: Primates Famili: Hominidae Subfamili: Homininae Genus: Paranthropus/ Australopithecus Spesies: P. robustus Nama binomial †Paranthropus robustusBroom, 1938 Paranthropus robustus Paranthropus robustus (atau Australopithecus Robustus) adalah spesies hominin. Fosilnya pertama kali ditemukan di Afrika bagian Selatan tahun 1938 oleh Robert Broom. Spesies ini m...

American baseball player and manager Not to be confused with Billy Joe Adcock. Baseball player Joe AdcockAdcock in 1954 with the Milwaukee BravesFirst baseman / Outfielder / ManagerBorn: (1927-10-30)October 30, 1927Coushatta, Louisiana, U.S.Died: May 3, 1999(1999-05-03) (aged 71)Coushatta, Louisiana, U.S.Batted: RightThrew: RightMLB debutApril 23, 1950, for the Cincinnati RedsLast MLB appearanceOctober 1, 1966, for the California AngelsMLB statisticsBatting ...

Universitas BhayangkaraRektorDrs. Suharto, SH, M.Hum Universitas Bhayangkara Surabaya adalah sebuah perguruan tinggi di Surabaya yang dikelola oleh Yayasan Brata Bhakti Daerah Jawa Timur. Fakultas Fakultas Ilmu Sosial dan Ilmu Politik Administrasi Negara, menjadi Prodi Administrasi Publik Ilmu Komunikasi Fakultas Hukum Ilmu Hukum S1 Magister Hukum S2 Fakultas Ekonomi Manajemen S1 Magister Manajemen S2 Akuntansi Ekonomi Pembangunan Fakultas Teknik Teknik Elektro Teknik Sipil Teknik Informatika...

Bruder Bernardus Hoecken, Bruder Pertama Kongregasi Bruder FIC.Lahir pada tahun 1809 dan meninggal pada tahun1880 Congregatio Fratrum Immaculatae Conceptionis Beatae Mariae Virginis (bahasa Indonesia: Kongregasi Para Bruder Santa Perawan Maria Yang Dikandung Tak Bernoda (Bruder FIC)) adalah sebuah Ordo di Gereja Katolik Roma yang didirikan oleh Mgr. Ludovicus Rutten.[1] Sementara itu, Ko-Pendiri, sekaligus bruder pertamanya adalah Bernardus Hoecken.[1] Kongregasi ini didirikan...

1st Canadian Parachute BattalionCap BadgeActive1942–1945CountryCanadaBranchCanadian ArmyTypeAirborne forcesRoleParachute infantrySizeBattalionPart of3rd Parachute Brigade (United Kingdom)Nickname(s)1 Can ParaColorsMaroon beretEngagements Operation Tonga Battle of the Bulge Operation Varsity Operation Overlord Battle honours Normandy Landing Dives Crossing The Rhine North-West Europe, 1944–1945 [1]CommandersNotablecommandersH.D. Proctor, July 1st, 1942–Sept. 7, 1942 G....

Soluzione salina preparata a partire da acqua e cloruro di sodio (sale da cucina). Una soluzione, in chimica, definisce una miscela omogenea in cui una o più sostanze sono contenute in una fase liquida, solida o gassosa; contiene particelle diverse mescolate e distribuite in modo uniforme nello spazio disponibile in modo che ogni volume di soluzione abbia la medesima composizione degli altri.[1] Quando, in una soluzione, un soluto è presente con atomi, ioni o molecole di dimensioni ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Setiles – news · newspapers · books · scholar · JSTOR (June 2016) (Learn how and when to remove this message) Place in Castile-La Mancha, SpainSetilesSetilesShow map of Province of GuadalajaraSetilesShow map of Castilla-La ManchaSetilesShow map of SpainCoordina...

مروان بن معاوية معلومات شخصية تاريخ الوفاة 193 هـ المذهب الفقهي أهل السنة والجماعة الحياة العملية العصر القرن الثاني للهجرة نظام المدرسة مدرسة الحديث المهنة عالم مسلم اللغة الأم العربية اللغات العربية مجال العمل علم الحديث تعديل مصدري - تعديل أبو عبد الله مروان �...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

British TV competition Season of television series The X FactorSeries 10Sam Bailey performing in Gibraltar in 2015.Hosted byDermot O'Leary (ITV)Judges Nicole Scherzinger Gary Barlow Sharon Osbourne Louis Walsh WinnerSam BaileyWinning mentorSharon OsbourneRunner-upNicholas McDonaldFinals venueWembley Arena ReleaseOriginal networkITVITV2 (The Xtra Factor)Original release31 August (2013-08-31) –15 December 2013 (2013-12-15)Series chronology← PreviousSeries 9Next →S...

豪栄道 豪太郎 場所入りする豪栄道基礎情報四股名 澤井 豪太郎→豪栄道 豪太郎本名 澤井 豪太郎愛称 ゴウタロウ、豪ちゃん、GAD[1][2]生年月日 (1986-04-06) 1986年4月6日(38歳)出身 大阪府寝屋川市身長 183cm体重 160kgBMI 47.26所属部屋 境川部屋得意技 右四つ・出し投げ・切り返し・外掛け・首投げ・右下手投げ成績現在の番付 引退最高位 東大関生涯戦歴 696勝493敗...

Великий восток ПортугалииВВПGrande Oriente Lusitano Дата основания 1882 год Тип Великий восток Число участников 2800 Город Лисабон, Португалия Медиафайлы на Викискладе Масонство Направления Регулярное масонство Либеральное масонство Масонство Принса Холла Терминология Сл...

Human settlement in WalesBeddauWelsh: Y BeddauBeddau SquareBeddauLocation within Rhondda Cynon TafPopulation4,156 (2011 Ward)[1]CommunityLlantrisantPrincipal areaRhondda Cynon TafPreserved countyMid GlamorganCountryWalesSovereign stateUnited KingdomPost townPONTYPRIDDPostcode districtCF38Dialling code01443PoliceSouth WalesFireSouth WalesAmbulanceWelsh UK ParliamentPontypriddSenedd Cymru – Welsh ParliamentPontypridd List of places UK Wales Rhondda ...

Ongoing COVID-19 viral pandemic in Toronto, Canada For effects of the pandemic in the province, see COVID-19 pandemic in Ontario. This article needs to be updated. Please help update this article to reflect recent events or newly available information. (October 2021) COVID-19 pandemic in TorontoDiseaseCOVID-19Virus strainSARS-CoV-2LocationToronto, Ontario, CanadaFirst outbreakWuhan, Hubei, ChinaIndex caseSunnybrook Hospital, TorontoArrival dateJanuary 22, 2020(4 years, 4 months and ...












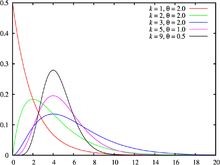


















![{\displaystyle {\text{E}}[X]=\alpha /\lambda }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e9d09169f4d133d994eaa85c554dac08a191b4b)
![{\displaystyle {\text{Var}}[X]={\frac {\alpha }{\lambda ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e324c06c297528e5d3a63f9176abcf9f13a6d3a8)

![{\displaystyle \operatorname {E} [X^{n}]={\frac {\alpha (\alpha +1)\cdots (\alpha +n-1)}{\lambda ^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d94f00117e39d9131ca916aaf8a81b019db436be)








![{\displaystyle \operatorname {E} [\ln(X)]=\psi (\alpha )-\ln(\lambda )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/851a0a36812edea4802f79b097400b31e049ad46)












