Círculo de Apolonio
|
Read other articles:

AIKATSU☆STARS! dan STAR☆ANIS AIKATSU☆STARS! adalah sebuah grup idola yang menampilkan lagu-lagu yang berkaitan dengan permainan Data Carddass Aikatsu! mula-mula dari seri tahun 2015, permainan Data Carddass Aikatsu Stars!, serta anime. Para anggota AIKATSU☆STARS! menyediakan suara vokal dari setidaknya satu karakter utama dalam alam Aikatsu Stars!, dan hanya disebut dengan nama panggilan mereka yang ditulis dalam bentuk hiragana. Mereka terkadang berkolaborasi dpada lagu-lagu dengan p...
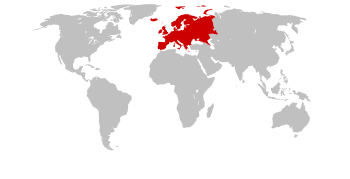
Europe beralih ke halaman ini. Untuk kegunaan lain dari Eropa atau Europe, lihat Eropa (disambiguasi). Untuk tokoh mitologi, lihat Europa. Untuk satelit alami Jupiter, lihat Europa (satelit). EropaLuas10.180.000 km2 (3.930.000 sq mi)Populasi741,907,867 (2024)Kepadatan penduduk34 per Km² (87 orang per mi²)DemonimEuropeans (Orang Eropa)Negara50 (dan 13 disengketakan)Dependensi Daftar ÅlandAkrotiri dan DhekeliaFaroeGibraltarGuernseyPulau ManJersey Negara non-PBB Daftar Ab...

His EminenceJoão Braz de AvizCardinal Prefect of the Congregation for Institutes of Consecrated Life and Societies of Apostolic LifeAppointed4 January 2011PredecessorFranc RodeOther post(s)Cardinal priest of Sant’Elena fuori Porta PrenestinaOrdersOrdination26 November 1972by Romeu AlbertiConsecration31 May 1994by Domingos Gabriel WisniewskiCreated cardinal18 February 2012by Pope Benedict XVIRankCardinal deacon (2012–22)Cardinal priest (2022–present)Personal detailsBornJoão ...

Pour les articles homonymes, voir Einstein et Marić. Mileva MarićMileva Marić en 1896.BiographieNaissance 19 décembre 1875Titel (royaume de Hongrie, Autriche-Hongrie)Décès 4 août 1948 (à 72 ans)Zurich (Suisse)Sépulture Cimetière de Nordheim (d)Nom dans la langue maternelle Милева МарићNationalité Royaume de HongrieDomiciles Smíchov (à partir de 1911), Novi SadFormation Université de ZurichÉcole polytechnique fédérale de ZurichUniversité de HeidelbergActivit�...

Portland Thorns FCBerdiri2012; 12 tahun lalu (2012)StadionProvidence ParkPortland, Oregon(Kapasitas: 25.218)Pemilik dan CEOMerritt PaulsonPelatih kepalaRhian WilkinsonLigaNational Women's Soccer League2021Challenge Cup: 1Musim regular: 1Playoff: Semi-finalSitus webSitus web resmi klub Kostum kandang Kostum tandang Musim ini Portland Thorns FC adalah klub sepak bola wanita profesional yang berbasis di Portland, Oregon. Dibentuk pada tahun 2012 dan turut serta dengan delapan tim lainn...

Tanda baca ‘’ “” Tanda baca elipsis … ... . . . ⋯ ᠁ ฯ garis miring, solidus / ⧸ ⁄ guilemet ‹ › « » hubung ‐ hubung tebal - koma , ، 、 kurung [ ] ( ) { } ⟨ ⟩ penyingkat ’ ' petik ‘ ’ “ ” ' ' pisah ‒ &#x...

The fountain at Argentomagus in 2009 The Roman city of Argentomagus was located in the Mersans plateau of central France, at the strategic point on the north bank of the river Creuse, where a Roman bridge once traversed. It was located at the crossing of two roads—Cenabum (Orléans) to Augustoritum (Limoges), and Limonum (Poitiers) to Avaricum (Bourges).[1] The Latin name of the city meant Silver Market. The modern town of Argenton takes its name from the ancient site of Argento...

安倍晋太郎安倍晋太郎(攝於1987年4月21日) 日本第112、113任外務大臣任期1982年11月27日—1986年7月22日总理中曾根康弘前任櫻内義雄继任倉成正 日本第42任通商產業大臣任期1981年11月30日—1982年11月27日总理鈴木善幸前任田中六助(日语:田中六助)继任山中貞則 日本第41任内閣官房長官任期1977年11月28日—1978年12月7日总理福田赳夫前任園田直继任田中六助(日语�...

В Википедии есть статьи о других людях с такой фамилией, см. Захарьин. Григорий Антонович Захарьин Дата рождения 8 (20) февраля 1829 Место рождения Пенза, Российская империя Дата смерти 23 декабря 1897 (4 января 1898) (68 лет) Место смерти Москва, Российская империя[1] Страна &...

Rubiana komune di Italia Tempat Negara berdaulatItaliaDaerah di ItaliaPiemonteKota metropolitan di ItaliaKota Metropolitan Turin NegaraItalia Ibu kotaRubiana PendudukTotal2.417 (2023 )GeografiLuas wilayah26,94 km² [convert: unit tak dikenal]Ketinggian640 m Berbatasan denganAlmese Condove Val della Torre Villar Dora Viù Caprie Informasi tambahanKode pos10040 Zona waktuUTC+1 UTC+2 Kode telepon011 ID ISTAT001229 Kode kadaster ItaliaH627 Lain-lainSitus webLaman resmi Rubiana adalah k...

1948 novel by Ruth Park The Harp in the South First UK edition (publ. Michael Joseph)AuthorRuth ParkLanguageEnglishGenreFictionPublisherAngus & Robertson, AustraliaPublication date1948Publication placeAustraliaMedia typePrintPages229 ppISBN0-14-010456-9Preceded by– Followed byPoor Man's Orange The Harp in the South is the debut novel by New Zealand-born Australian author Ruth Park. Published in 1948, it portrays the life of a Catholic Irish Australian family li...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) أستراليا كأس العالم 2006 الاتحاد المشرف اتحاد أستراليا لكرة القدم البلد المضيف ألمانيا المدرب غوس هيدي...

2016年夏季奥林匹克运动会巴布亚新几内亚代表團巴布亚新几内亚国旗IOC編碼PNGNOC巴布亚新几内亚奥林匹克委员会網站www.pngolympic.org(英文)2016年夏季奥林匹克运动会(里約熱內盧)2016年8月5日至8月21日運動員8參賽項目6个大项旗手开幕式:Ryan Pini(游泳)[1]闭幕式:Samantha Kassman(跆拳道)[2]历届奥林匹克运动会参赛记录(总结)夏季奥林匹克运动会1976198019841988...

Grand Prix Belgia 2004 Lomba ke-14 dari 18 dalam Formula Satu musim 2004← Lomba sebelumnyaLomba berikutnya → Detail perlombaanTanggal 29 Agustus 2004Nama resmi Formula 1 Belgian Grand Prix 2004[1]Lokasi Circuit de Spa-FrancorchampsSirkuit Fasilitas balap permanenPanjang sirkuit 6.976 km (4.335 mi)Jarak tempuh 44 putaran, 306.927 km (190.716 mi)Cuaca Kering dengan temperatur mencapai 15 °C (59 °F)[2]Posisi polePembalap Jarno Trulli RenaultWak...

أمريكان آيدولAmerican Idol (بالإنجليزية) الشعارمعلومات عامةالنوع singing talent show (en) تأليف سيمون فولر إخراج بروس غاورز[1] — Ken Warwick (en) — شاين دريك — نايجل ليثجو تقديم رايان سيكرست — Brian Dunkleman (en) — بوبي بونز بلد الأصل الولايات المتحدة[2] لغة العمل الإنجليزية عدد المواسم/الأجز...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. La traduction de cet article ou de cette section doit être revue (septembre 2017). Le contenu est difficilement compréhensible vu les erreurs de traduction, qui sont peut-être dues à l'utilisation d'un logiciel de traduction automatique. Discutez des points à améliorer en page de discussion ou modifiez l'article. Le mot probabilité a été utilisé dans une variété de domaines depuis qu'il a été appliq...

Formal assembly (typically ecclesiastical or academic) Convocations redirects here. For the Sufjan Stevens album, see Convocations (album). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Convocation – news · newspapers · books · scholar · JSTOR (October 2011) (Learn how and when to remove this message) Stud...

高速自動車国道(有料/無料) E42 紀勢自動車道 地図 路線延長 94.6 km三重県区間 55.3 km和歌山県区間 39.3 km 開通年 2006年(平成18年) - 起点 三重県多気郡多気町(勢和多気JCT)和歌山県田辺市(南紀田辺IC) 終点 三重県尾鷲市(尾鷲北IC)和歌山県西牟婁郡すさみ町(すさみ南IC) 接続する主な道路(記法) 記事参照 ■テンプレート(■ノート ■使い方) ■PJ道路 紀勢�...

Russian Imperial Minister of War from 1898 to 1904 This article is missing information about 1900 Amur anti-Chinese pogroms. Please expand the article to include this information. Further details may exist on the talk page. (April 2024) Kuropatkin redirects here. For the village in Azerbaijan, see Kuropatkino. In this name that follows Eastern Slavic naming customs, the patronymic is Nikolayevich and the family name is Kuropatkin. Aleksey KuropatkinАлексей КуропаткинGener...

Son of Persian king Darius I (died 480 BC). This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Hyperanthes – news · newspapers · books · scholar · JSTOR (January 2020) Hyperanthes (Ancient Greek: Ὑπεράνθης) was a son of Darius the Great of Persia by Phratagune, and brother to Xerxes I. He wa...

















