Aplicación logística
|
Read other articles:
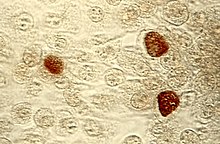
Untuk penyakit pada manusia, lihat Infeksi chlamydia. Chlamydia Badan inklusi C. trachomatis (coklat) pada kultur sel McCoy. Klasifikasi ilmiah Domain: Bakteri Filum: Chlamydiae Kelas: Chlamydiae Ordo: Chlamydiales Famili: Chlamydiaceae Genus: Chlamydia Spesies Chlamydia avium Sachse dkk. 2015[1] Chlamydia felis Sachse dkk. 2015[1] Chlamydia gallinacea Sachse dkk. 2015[1] Chlamydia muridarum Everett dkk. 1999Chlamydophila pecorum Fukushi & Hirai 1992, gen. nov. Eve...

Untuk kegunaan lain, lihat Get Married (disambiguasi). Get Married 3poster filmSutradaraMonty TiwaProduserChand Parwez ServiaDitulis olehCassandra MassardiPemeranNirina ZubirFedi NurilAminkRinggo AgusDesta MahendraMeriam BellinaJaja MihardjaIra WibowoRatna RiantiarnoDistributorStarvision PlusTanggal rilis25 Agustus 2011Negara IndonesiaPrekuelGet Married 2 Get Married 3 merupakan film drama/komedi Indonesia yang dirilis pada 25 Agustus 2011 yang disutradarai oleh Monty Tiwa serta dibintangi ol...

Qazaqstan Prem'er Ligasy 2017 Competizione Qazaqstan Prem'er Ligasy Sport Calcio Edizione 26ª Organizzatore KFF Date dall'8 marzo 2017al 9 novembre 2017 Luogo Kazakistan Partecipanti 12 Risultati Vincitore Astana(4º titolo) Retrocessioni Taraz Oqjetpes Statistiche Miglior giocatore Gerard Gohou Miglior marcatore Gerard Gohou (24) Incontri disputati 198 Gol segnati 488 (2,46 per incontro) Cronologia della competizione 2016 2018 Manuale La Qazaqstan ...

South African fashion designer Gert-Johan Coetzee Gert-Johan Coetzee (born 18 November 1987), is a South African fashion artist. His fashion atelier is based in Linden, Johannesburg in Gauteng province. He specialises in couture red carpet gowns, he also designs ready-to-wear range . Coetzee is known for dressing South African and international celebrities at red-carpet events.[1] Early life and education Coetzee was born in Koster, North West Province. His love for fashion started at...

ChellahSala ColoniaشالةBagian dari Chellah/Sala ColoniaLokasi di MarokoLokasiRabat, Rabat-Salé-Zemmour-Zaer, MarokoKoordinat34°00′24″N 06°49′13″W / 34.00667°N 6.82028°W / 34.00667; -6.82028Koordinat: 34°00′24″N 06°49′13″W / 34.00667°N 6.82028°W / 34.00667; -6.82028JenisPermukiman dan nekropolisSejarahDitinggalkan1154 Chellah (Arab: شالةcode: ar is deprecated ) atau Sala Colonia adalah nekropolis dan situs Romawi ...

Hideki Yukawa 湯川 秀樹Lahir(1907-01-23)23 Januari 1907Tokyo, JapanMeninggal8 September 1981(1981-09-08) (umur 74)Kyoto, JapanKebangsaanJapanAlmamaterUniversitas Imperial KyotoPenghargaanPenghargaan Nobel dalam Fisika (1949)Karier ilmiahBidangFisika TeoretisInstitusiUniversitas Imperial Osaka Universitas Imperial Kyoto Osaka Imperial University Kyoto Imperial University Imperial University of Tokyo Institute for Advanced Study Universitas imperial Tokyo Institut untuk Pelajaran Lanj...

The PhantomTitle page of prompt bookWritten byDion BoucicaultDate premieredJune 14, 1852 (1852-06-14)Place premieredPrincess's Theatre, LondonOriginal languageEnglish The Phantom is a two act melodrama written by Dion Boucicault. It was originally titled The Vampire when it was first performed at the Princess's Theatre in London in 1852. Boucicault renamed it The Phantom when he went to the United States, where it opened in Philadelphia in 1856.[1] The play tells the st...

American baseball player (born 1987) For other people named Justin Wilson, see Justin Wilson (disambiguation). Baseball player Justin WilsonWilson with the Mets in 2019Cincinnati Reds – No. 32PitcherBorn: (1987-08-18) August 18, 1987 (age 36)Anaheim, California, U.S.Bats: LeftThrows: LeftMLB debutAugust 20, 2012, for the Pittsburgh PiratesMLB statistics (through April 24, 2024)Win–loss record34–24Earned run average3.43Strikeouts514 Teams Pittsburgh Pirates (2012–20...

نينجا ثيورينينجا ثيوريالشعارمعلومات عامةالبلد المملكة المتحدة التأسيس 2004النوع مطور لعبة فيديوالشكل القانوني شركة عمومية محدودة المقر الرئيسي كامبريدج ، إنجلترا،المملكة المتحدةموقع الويب ninjatheory.com (الإنجليزية) المنظومة الاقتصاديةالشركة الأم إكس بوكس غيم ستوديوز ال�...

Road in England This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: A584 road – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and when to remove this message) A584Queen's Promenade, BisphamRoute informationLength19 mi (31 km)LocationCountryUnited KingdomConstituent countryEngland Road netw...

Questa voce o sezione sull'argomento musica classica è ritenuta da controllare. Motivo: creata da utente infinitato (Wp:Utenti problematici/Colombaros), da ripulire dalla minutaglia non enciclopedica Partecipa alla discussione e/o correggi la voce. Segui i suggerimenti del progetto di riferimento. On the TownLingua originaleInglese StatoStati Uniti d'America Anno1944 Prima rappr.28 dicembre 1944 al Teatro Adelphi (New York) CompagniaBroadway theatre GenereMusical RegiaGeorge Abbott Sog...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

In telecommunication, a ternary signal is a signal that can assume, at any given instant, one of three states or significant conditions, such as power level, phase position, pulse duration, or frequency. Examples of ternary signals are (a) a pulse that can have a positive, zero, or negative voltage value at any given instant (PAM-3), (b) a sine wave that can assume phases of 0°, 120°, or 240° relative to a clock pulse (3-PSK), and (c) a carrier signal that can assume any one of three diffe...

Medical conditionPiebaldismOther namesPBT[1]This condition affects melanocyte developmentSpecialtyDermatology Piebaldism refers to the absence of mature melanin-forming cells (melanocytes) in certain areas of the skin and hair. It is a rare autosomal dominant disorder of melanocyte development.[2]: 867 Common characteristics include a congenital white forelock, scattered normal pigmented and hypopigmented macules and a triangular shaped depigmented patch on th...

العلاقات السودانية النمساوية السودان النمسا السودان النمسا تعديل مصدري - تعديل العلاقات السودانية النمساوية هي العلاقات الثنائية التي تجمع بين السودان والنمسا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقا...

Bruno BruinsBruins pada tahun 2018 Menteri KesehatanMasa jabatan26 Oktober 2017 – 19 Maret 2020Perdana MenteriMark RuttePenggantiMartin van RijnSekretaris Negara untuk Pendidikan, Budaya dan SainsMasa jabatan29 Juni 2006 – 22 Februari 2007Menjabat bersama Medy van der Laan (2006)Perdana MenteriJan Peter BalkenendePendahuluMark RuttePenggantiMarja van Bijsterveldt Sharon DijksmaWalikota Leidschendam-VoorburgMasa jabatan22 Februari 2007 – 1 November 2007...

Bagian dari rangkaian tentang Topik Anti perang Menentang... Perang Irak Perang melawan Terorisme Perang Afganistan Perang Vietnam Perang 1812 Perang Saudara Amerika Perang Boer Kedua Agen-agen oposisi Organisasi anti perang Penentang karena nurani Penghindar wajib militer Gerakan perdamaian Gereja-gereja damai Ideologi terkait Anti militerisme Anti imperialisme Appeasement Pasifisme Media Buku Film Lagu protes Politics PortalKotak ini: lihatbicarasunting Arah Pasifisme adalah perlawanan ter...

تفتقر سيرة هذه الشخصية الحيّة إلى الاستشهاد بمصدر موثوق به يمكن التحقق منه. فضلاً، ساهم في تطويرها من خلال إضافة مصادر موثوق بها. في سير الأحياء، يُزال المحتوى فوراً إذا كان من غير مصدر يدعمه أو إذا كان المصدر المُستشهد به مشكوكاً بأمره. (فبراير 2016) أوليفر ستون Oliver Stone معلوما...

1960 Libyan general election ← 1956 17 January 1960 1964 → All 55 seats in the House of Representatives Party % Seats +/– Independents 100 55 0 This lists parties that won seats. See the complete results below. Prime Minister before Prime Minister after Abdul Majid Kabar Abdul Majid Kabar Politics of Libya Member State of the Arab League Constitution 2017 draft constitution 2011 Constitutional Declaration (Basic Law) 1977 People's Authority 1969 Constitution 1951 Const...

2002 EP by Amalgamated Sons of RestAmalgamated Sons of RestEP by Amalgamated Sons of RestReleasedSeptember 1, 2002GenreFolkLabelGalaxia Professional ratingsReview scoresSourceRatingAllMusic [1]Pitchfork Media(5.9/10) [2] Amalgamated Sons of Rest is the name of a one-off project by American songwriters Will Oldham and Jason Molina, along with Scottish colleague Alasdair Roberts. The collaboration yielded one eponymous EP, released in 2002 on Galaxia Records, and a song,...






















