Plurĉelo
|
Read other articles:

Menara Smaiholm, menunjukkan dinding barkim pada bagian depan Barmkin, juga dieja barmekin atau barnekin, adalah kata Skotlandia yang mengacu pada bentuk kandang abad pertengahan dan kemudian untuk pertahanan, biasanya ditemukan di sekitar kastel yang lebih kecil,rumah menara, menara pele, dan rumah bastle di Skotlandia, dan utara Inggris. Telah dikemukakan bahwa secara etimologis kata tersebut mungkin merupakan pengurangan dari kata barbican atau berm.[1] Barmkin akan memiliki bangun...

James Edward Allchin (kelahiran Grand Rapids, Michigan, Amerika Serikat pada tahun 1951) adalah co-President Platform Products and Services Group (semacam Divisi Customer Relationship) dari Perusahaan Microsoft, yang bertanggung jawab atas pelayanan sistem operasi, produk streaming media, dan jasa internet. Allchin direkrut oleh Bill Gates setelah pendekatan selama setahun sebelum akhirnya setuju untuk bergabung dengan Microsoft pada tahun 1990. Allchin menjabat sebagai co-President Platform ...
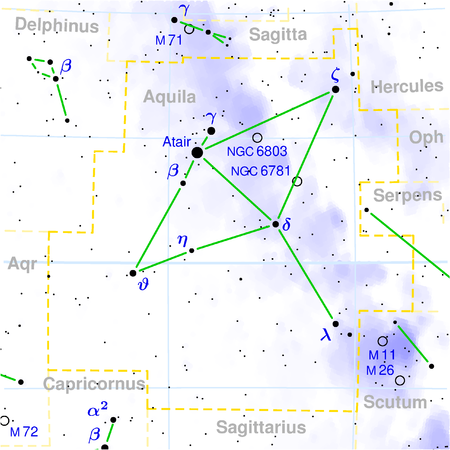
δ Aquilae Data pengamatan Epos J2000 Ekuinoks J2000 Rasi bintang Aquila Asensio rekta 19h 25m 29.9005s Deklinasi +03° 06′ 53.191″ Magnitudo tampak (V) 3.4 Ciri-ciri Kelas spektrum F0IV Indeks warna U−B 0.04 Indeks warna B−V 0.32 Indeks warna R−I 0.16 Jenis variabel Bintang variabel AstrometriKecepatan radial (Rv)-30.1 km/sGerak diri (μ) RA: 253.07 mdb/thn Dek.: 80.67 mdb/thn Paralaks (π)65,05±0,81&...

Meitantei Konan Meikyū no KurosurōdoSutradaraKenji KodamaProduserMichihiko SuwaDitulis olehKazunari KochiPenata musikKatsuo OnoDistributorTohoTanggal rilis19 April 2003[1]Durasi108 menitNegara JepangBahasaBahasa JepangPrekuelThe Phantom of Baker StreetSekuelMagician of the Silver Sky Meitantei Konan Meikyū no Kurosurōdo (名探偵コナン 迷宮の十字路code: ja is deprecated ) adalah film tuturan ke-7 dari seri Detektif Conan. Film ini dirlis pada 19 April 2003. ...

Three-Ring MarriageSutradaraMarshall NeilanProduserHenry HobartDitulis olehThomas J. Geraghty Harvey F. Thew Dixie WillsonPemeranMary Astor Lloyd Hughes Lawford DavidsonSinematograferDavid KessonPenyuntingStuart HeislerPerusahaanproduksiFirst National PicturesDistributorFirst National PicturesTanggal rilis 10 Juni 1928 (1928-06-10) Durasi60 menitNegaraAmerika SerikatBahasaBisu (intertitel Inggris) Three-Ring Marriage juga dikenal sebagai 3-Ring Marriage adalah sebuah film drama bisu Ame...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: History of vehicle registration plates of the Philippines – news · newspapers · books · scholar · JSTOR (October 2020) Philippine vehicle registration plates have a long history. The earliest license plates were introduced around 1912 with the introd...

Pertempuran KyivBagian dari Serangan Kyiv dan Invasi Rusia ke Ukraina 2022Rusia menyerang Menara TV KievTanggal25 Februari 2022 – 31 Maret 2022LokasiKyiv, UkrainaHasil Kemenangan UkrainaPihak terlibat UkrainaDidukung oleh: Oposisi Belarus RusiaTokoh dan pemimpin Oleksandr Syrskyi Vitali Klitschko Tidak diketahuiPasukan Angkatan Bersenjata Ukraina Angkatan Darat Ukraina Brigade Mekanik ke-72 Brigade Perlindungan Staf Umum ke-101[1] Brigade Terpisah Presidensial Batalyon D...

Spanish law enforcement association Posada de la Santa Hermandad, in Toledo, Spain, dating from the 15th century, now a historic site Santa Hermandad (Spanish: [ˈsanta eɾmanˈdað], lit. holy brotherhood) was a type of military peacekeeping association of armed individuals, which became characteristic of municipal life in medieval Spain, especially in Castile. Modern hermandades in Spain, some of which evolved from medieval origins, are now for the most part religious confraternitie...

Pasukan Inggris mendarat dari sebuah helikopter Westland Wessex pada sebuah operasi di Borneo pada Agustus 1964. Konfrontasi Indonesia–Malaysia dimulai pada awal 1963 setelah penentangan Indonesia terhadap pembentukan Malaysia. Serangan-serangan Indonesia awal ke Malaysia Timur sangat ditunjang para sukarelawan lokal yang dilatih oleh Angkatan Darat Indonesia. Seiring berjalannya waktu, pasukan infiltrasi menjadi makin terorganisir dengan pengerahan jumlah pasukan Indonesia yang lebih besar...

Questa voce o sezione deve essere rivista e aggiornata appena possibile. Sembra infatti che questa voce contenga informazioni superate e/o obsolete. Se puoi, contribuisci ad aggiornarla. Tragedia di piazza San CarloPiazza San Carlo TipoDisastro dovuto alla fuga di persone Data3 giugno 201722:15 circa LuogoTorino Stato Italia Coordinate45°04′03.83″N 7°40′57.32″E / 45.06773°N 7.68259°E45.06773; 7.68259Coordinate: 45°04′03.83″N 7°40′57.32″E / &...

Questa voce o sezione sull'argomento calciatori italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: Una non basta Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Giancarlo Oddi Oddi con la maglia della Lazio Nazionalità Italia Altezza 176 cm Peso 72 kg Calcio Ruolo Allenatore (ex difensore) Termine carriera 1984 - giocatore Carrie...

Pierre-Marie Théas Biographie Nom de naissance Pierre Théas-Laban Naissance 14 septembre 1894 à Barzun (France)Barzun Ordination sacerdotale 26 septembre 1920 Décès 3 avril 1977 (à 82 ans)Pau Évêque de l'Église catholique Ordination épiscopale 3 octobre 1940 par Edmond Vansteenberghe Évêque de Tarbes et Lourdes 17 février 1947 – 12 février 1970 Georges Choquet Henri Donze Évêque de Montauban 26 juillet 1940 – 17 février 1947 Eli Durand Louis de Courrèges d'Ustou «...

Canadian politician MayorÉdouard-Raymond Fabre6th Mayor of MontrealIn office1849–1851Preceded byJoseph BourretSucceeded byCharles WilsonConstituencyEast Personal detailsBorn(1799-09-15)15 September 1799Montreal, Lower CanadaDied16 July 1854(1854-07-16) (aged 54)Montreal, Canada EastResting placeNotre Dame des Neiges CemeteryChildrenHector Fabre, Édouard-Charles FabreProfessionbookseller Édouard-Raymond Fabre (15 September 1799 – 16 July 1854) was a Canadian politician and book...

1500s and 1600s outbreak This article is about the alleged poisoning. For the Tito & Tarantula album, see Tarantism (album). Lycosa tarantula carrying her offspring Tarantism is a form of hysteric behaviour originating in Southern Italy, popularly believed to result from the bite of the wolf spider Lycosa tarantula (distinct from the broad class of spiders also called tarantulas). A better[clarification needed] candidate cause is Latrodectus tredecimguttatus, commonly known as the...

United States Civil War military unit 15th Connecticut Infantry RegimentActiveAugust 25, 1862 – July 12, 1865CountryUnited StatesAllegianceUnionBranchInfantryEngagementsBattle of FredericksburgBattle of Wyse ForkMilitary unit Connecticut U.S. Volunteer Infantry Regiments 1861-1865 Previous Next 14th Connecticut Infantry Regiment 16th Connecticut Infantry Regiment Col. Dexter R. Wright in his later years Capt. Theodore Rich Davis (1839–1890), Company B, 15th Connecticut The 15th Connecticu...

Deaf sign language of Afghanistan Afghan Sign LanguageJalalabad Sign LanguageNative toAfghanistanNative speakers190,000 (2021)[1]Language familyLanguage isolateLanguage codesISO 639-3afgGlottologafgh1239 Afghan Sign Language (Dari: زبان اشاره افغانستانی) is the deaf sign language of Jalalabad in eastern Afghanistan, possibly with some presence in Kabul. It has been encouraged in the country's only school for the deaf, and derives from the Deaf-community si...

VenoncomuneVenon – Veduta LocalizzazioneStato Francia Regione Normandia Dipartimento Eure ArrondissementÉvreux CantoneLe Neubourg TerritorioCoordinate49°10′N 1°03′E49°10′N, 1°03′E (Venon) Superficie5,1 km² Abitanti304[1] (2009) Densità59,61 ab./km² Altre informazioniCod. postale27110 Fuso orarioUTC+1 Codice INSEE27677 CartografiaVenon Sito istituzionaleModifica dati su Wikidata · Manuale Venon è un comune francese di 304 abitanti situato ne...
Israeli television series HaDugmaniotGenreReality televisionCreated byTyra BanksPresented byGalit GutmannJudgesGalit Gutmann (1-3)Miki Buganim (1-3)Sefi Shaked (2-3)Stella Amar (3)Elimor Zilberman (1-3)Yael Reich (2)Betty Rockaway (1-2)Eshel Ezer (1)Shiraz Tal (1)Country of originIsraelNo. of episodes42ProductionRunning time80 minutesOriginal releaseNetworkChannel 10Release21 February 2005 (2005-02-21) –22 April 2008 (2008-04-22) HaDugmaniot (Hebrew: הדוגמניות; Engli...

Untuk bekas partai politik pimpinan Alex Goldfarb, lihat Atid (partai politik). Yesh Atid יש עתידKetua umumYair LapidDibentukJanuary 2012 (January 2012)Kantor pusatTel AvivIdeologiLiberalisme[1]Sekulerisme[2]Liberalisme ekonomi[3][4]Zionisme Liberal[5] Solusi dua negara[6][7]Posisi politikTengah[3]Afiliasi nasionalBiru & Putih (2019–)Afiliasi internasionalLiberal InternationalKnesset24 / 120Anggota Knesset t...

Earthenware vessel of Provence, France For other uses, see Tian (disambiguation). Tian D'aubergine served inside a tian A tian is an earthenware vessel of Provence used both for cooking and serving. It is also the name of the dish prepared in it and baked in an oven.[1] Tian comes from the ancient Provençal word designating a terracotta cooking dish, and is also used to refer to food prepared in it. The word comes from the ancient Greek teganon (frying pan).[2] The classic ve...