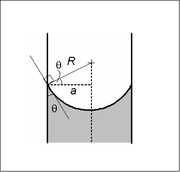
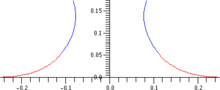
Young–Laplace equation
|
Read other articles:

Wakil Presiden AS Mike Pence dengan para anggota tim SWAT Broward County, Florida pada 30 November 2018; pria di kiri gambar mengenakan simbol Q berwarna merah-hitam, simbol dari QAnon. QAnon (/kjuːəˈnɒn/) adalah sebuah teori konspirasi sayap kanan jauh[6] yang menyatakan bahwa terdapat rencana rahasia yang dilakukan oleh negara rahasia terhadap Presiden AS Donald Trump dan para pendukungnya.[7] Teori tersebut dimulai dengan sebuah pos Oktober 2017 pada papan gambar 4chan ...

Atsuko Maeda前田敦子Atsuko Maeda pada tahun 2016.LahirMaeda Atsuko (前田敦子code: ja is deprecated )10 Juli 1991 (umur 32)Ichikawa, Prefektur ChibaKebangsaanJepangNama lainAcchanPekerjaanArtisidolapenyanyiAnggota AKB48 (2005-2012)Dikenal atasPeringkat 1 (Center) — Pemilihan Member Single ke-13 AKB48 (2009)Peringkat 2 (Senbatsu) — Pemilihan Member Single ke-17 AKB48 (2010)Peringkat 1 (Center) — Pemilihan Member Single ke-22 AKB48 (2011)Kota asalIchikawa, Prefektur...

Island in the Bailiwick of Guernsey in the Channel Islands This article is about the Channel Island called Herm. For other uses, see Herm (disambiguation). Place in United KingdomHermHaerme (Guernésiais)Part of Guernsey, Bailiwick of Guernsey FlagCoat of armsAnthem: Sarnia Cherie (Guernsey)Sovereign stateUnited Kingdom[a]Crown DependencyGuernseyParishSaint Peter PortOfficial languagesEnglishGuernésiaisFrenchGovernmentParliamentary constitutional monarchy• Duke Char...

Mariusz Lewandowski Informasi pribadiNama lengkap Mariusz LewandowskiTanggal lahir 18 Mei 1979 (umur 44)Tempat lahir Legnica, PolandiaTinggi 1,84 m (6 ft 1⁄2 in)Posisi bermain GelandangInformasi klubKlub saat ini PFC SevastopolNomor 18Karier junior Zagłębie LubinKarier senior*Tahun Tim Tampil (Gol)1996–1999 Zagłębie Lubin 36 (0)2000–2001 Dyskobolia Grodzisk 40 (2)2001–2010 Shakhtar Donetsk 174 (21)2010– Sevastopol 25 (6)Tim nasional‡2002– Polandia 65...

Italian footballer Raffaele Pucino Personal informationDate of birth (1991-05-03) 3 May 1991 (age 32)Place of birth Caserta, ItalyHeight 1.83 m (6 ft 0 in)Position(s) Right back, centre backTeam informationCurrent team BariNumber 25Youth career Boys Caserta Napoli Empoli Casertana Atletico NolaSenior career*Years Team Apps (Gls)2009–2011 Alessandria 44 (0)2011–2013 Varese 69 (3)2013–2014 Sassuolo 3 (0)2014–2017 Chievo 0 (0)2014–2015 → Pescara (loan) 36 (0)2015�...

Edition of the NBA Finals 2023 NBA Finals TeamCoachWins Denver Nuggets Michael Malone 4 Miami Heat Erik Spoelstra 1 DatesJune 1–12MVPNikola Jokić (Denver Nuggets)Eastern FinalsHeat defeated Celtics, 4–3Western FinalsNuggets defeated Lakers, 4–0 ← 2022 NBA Finals 2024 → The 2023 NBA Finals was the championship series of the National Basketball Association (NBA)'s 2022–23 season and conclusion to the season's playoffs. The best-of-seven playoffs was played between...

River in Wales which flows into Cardiff Bay Not to be confused with River Taf. River TaffThe Taff flowing through LlandaffNative nameAfon Taf (Welsh)LocationCountryWalesHistoric countyGlamorganUnitary AuthorityMerthyr Tydfil, Rhondda Cynon Taf, CardiffSettlementsMerthyr Tydfil, Treharris, Pontypridd, CardiffPhysical characteristicsSource • locationCefn-coed-y-cymmer, Merthyr Tydfil, Wales Length67 km (42 mi)[1]Discharge • ...

坐标:43°11′38″N 71°34′21″W / 43.1938516°N 71.5723953°W / 43.1938516; -71.5723953 此條目需要补充更多来源。 (2017年5月21日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:新罕布什尔州 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源...

Version of the Type 205 submarine For the older submarine called Kobben (1909–1926), see HNoMS Kobben (1909). Kobben-class profile HNoMs Utstein, now a museum ship Class overview BuildersNordseewerke GmbH Operators Royal Norwegian Navy Royal Danish Navy Polish Navy Succeeded byUla class SubclassesTumleren class Built1963–1966 In commission1964–2021 Completed15 Active0 Laid up3 Preserved5 (2 in Poland, 2 in Denmark, 1 in Norway) General characteristics TypeCoastal ...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2015) هجمات 19 مارس 2013 في العراق كانت سلسلة من التفجيرات المنسقة وعمليات إطلاق النار في العاصمة بغداد وعدد من المدن الكبرى في الشمال والمناطق الوسطى من البلاد. قتل...

نسبة التحضر عالميًا في 2015. يشير التَمَدُّنُ أو التحضر إلى التحول السكاني من المناطق الريفية إلى الحضرية، والزيادة التدريجية في نسبة السكان القاطنين في المناطق الحضرية، والوسائل التي يتكيف بها كل مجتمع مع هذا التغيير.[1] وهي العملية التي يغلب عليها طابع تشكيل المدن وال�...

Mobile food stand selling hot dogs A hot dog cart in New York City Part of a series onAmerican cuisine Regional cuisines Northeastern New England New Jersey New York City Philadelphia Midwestern Chicago Michigan North Dakota Ohio Omaha St. Louis Wisconsin Mid-Atlantic Baltimore Pittsburgh Southern (list) Atlanta Cajun Floribbean Kentucky Louisiana Creole Lowcountry Houston New Orleans Texas Tex-Mex Western California California fusion Los Angeles Pacific Northwest Rocky Mountain Southwestern ...

Unit of power with different values For other uses, see Horsepower (disambiguation). HorsepowerOne imperial horsepower lifts 550 pounds (250 kg) by 1 foot (30 cm) in 1 second.General informationUnit ofpowerSymbolhp Horsepower (hp) is a unit of measurement of power, or the rate at which work is done, usually in reference to the output of engines or motors. There are many different standards and types of horsepower. Two common definitions used today are the imperial horsepow...

USNS Waccamaw (T-AO-109) Ships of the United States NavyShips in current service Current ships Ships grouped alphabetically A–B C D–F G–H I–K L M N–O P Q–R S T–V W–Z Ships grouped by type Aircraft carriers Airships Amphibious warfare ships Auxiliaries Battlecruisers Battleships Cruisers Destroyers Destroyer escorts Destroyer leaders Escort carriers Frigates Hospital ships Littoral combat ships Mine warfare vessels Monitors Oilers Patrol vessels Registered civilian vessels Sai...

Historic church in South Dakota, United States United States historic placeChurch of the Immaculate ConceptionU.S. National Register of Historic Places The church in 2017Show map of South DakotaShow map of the United StatesLocation918 5th St.Rapid City, South DakotaCoordinates44°4′33″N 103°13′31″W / 44.07583°N 103.22528°W / 44.07583; -103.22528Area1 acre (0.40 ha)Built1902 (1902)Architectural styleRomanesqueNRHP reference No.7500172...

دراسات المجتمعصنف فرعي من علوم اجتماعية جزء من urban sociology and community studies (en) تعديل - تعديل مصدري - تعديل ويكي بيانات دراسات المجتمع هي مجال أكاديمي يستند إلى علم الاجتماع وعلم الإنسان ومناهج البحث الاجتماعي لوصف الأعراق البشرية وملاحظة المشارك في دراسة المجتمع. في البيئات الأكا�...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مارس 2023) فرانك كوفاكس معلومات شخصية الميلاد 4 ديسمبر 1919(1919-12-04)أوكلاند الوفاة فبراير 1990 (70&...

Gianfranco Ganau Presidente del Consiglio regionale della SardegnaDurata mandato20 marzo 2014 –9 aprile 2019 PredecessoreClaudia Lombardo SuccessoreMichele Pais Sindaco di SassariDurata mandato9 maggio 2005 –28 marzo 2014 PredecessoreNanni Campus SuccessoreGuido Sechi(commissario straordinario) Dati generaliPartito politicoPartito Democratico (dal 2007)In precedenza:PDS (1991-1998)DS (1998-2007) Titolo di studioLaurea in medicina e chirurgia Univ...

城市故事City Japes类型處境喜劇主演溫兆倫、曾近榮、丁 茵、何美婷、梁思浩、郭晉安、羅嘉良、劉淑華、唐麗球、何偉龍、彭健新、吳茜薇集数455主题曲Plucky Fella [1]作曲David Snell制作拍摄/制作年份1986年-1988年制作统筹黃 令、郭靜霞监制梁材遠编审岑國榮、韋家輝、余詠珊、鄧特希拍攝地點 英屬香港制作公司香港電視廣播有限公司無綫電視翡翠台首播 播出日�...

Koko Prasetyo DarkuncoroInformasi pribadiLahirOctober 2, 1981 (1981-10-02) (usia 42)Jakarta, Indonesia Rekor medali Voli pantai putra Mewakili Indonesia Pesta Olahraga Asia 2002 Busan Pantai putra Pesta Olahraga Pantai Asia 2008 Bali Pantai putra 2012 Haiyang Pantai putra 2014 Phuket Pantai putra Kejuaraan Asia 2005 Songkhla Pantai putra 2006 Pulau Kish Pantai putra 2007 Songkhla Pantai putra 2008 Hyderabad Pantai putra 2010 Haikou Pantai putra 2012 Haikou Pantai putra Pesta Olahra...