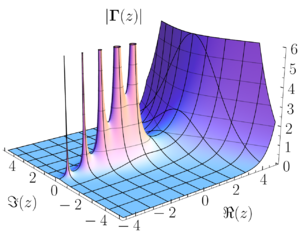
Schwarz lemma
|
Read other articles:

Untuk putranya, kimiawan dan geolog Amerika Serikat, lihat Benjamin Silliman Jr. Untuk pengacara dan politikus dari New York, lihat Benjamin D. Silliman. Benjamin SillimanSilliman pada sekitar tahun 1850Lahir8 Agustus 1779Trumbull, Connecticut, Amerika SerikatMeninggal24 November 1864(1864-11-24) (umur 85)New Haven, Connecticut, Amerika SerikatKebangsaanAmerika SerikatAlmamaterUniversitas YaleDikenal atasDistilasi minyak bumiPenghargaanNational Academy of SciencesKarier ilmiahBidangKimia...

Chloris Chloris barbata Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Plantae Upakerajaan: Trachaeophyta Divisi: Magnoliophyta Kelas: Liliopsida Subkelas: Commelinidae Ordo: Poales Famili: Poaceae Subfamili: Chloridoideae Tribus: Cynodonteae Subtribus: Eleusininae Genus: ChlorisSw. Spesies tipe Chloris cruciata(L.) Sw.[1] Spesies Lihat teks Sinonim[2] Agrostomia Cerv. Chlorostis Raf. Pterochloris (A.Camus) A.Camus Chloris adalah genus rumput monofiletik yang tersebar luas &a...

Aroutz 1 הערוץ הראשוןCaractéristiquesCréation 2 mai 1968Disparition 10 mai 2017Propriétaire Israel Broadcasting AuthorityLangue HébreuPays IsraëlStatut Généraliste nationale publiqueSiège social Israel Broadcasting Authority 161 Jaffa Road JérusalemAncien nom HaTelevizia HaIsraelit (1968-1994)Site web iba.org.ilmodifier - modifier le code - modifier Wikidata Aroutz 1 (en hébreu הערוץ הראשון, HaArouts HaRishon, litt. « La première chaîne » ; e...

Dimitri Foulquier Informasi pribadiNama lengkap Dimitri FoulquierTanggal lahir 23 Maret 1993 (umur 31)Tempat lahir Sarcelles, PrancisTinggi 1,84 m (6 ft 0 in)Posisi bermain Bek kananInformasi klubKlub saat ini Granada (pinjaman dari Rennes)Nomor 22Karier junior2000–2001 Capesterre Belle-Eau2001–2007 Marquisat Capesterre2007–2011 RennesKarier senior*Tahun Tim Tampil (Gol)2011– Rennes 17 (0)2013– → Granada (pinjaman) 8 (0)Tim nasional‡2010–2011 Prancis U-18 7 (0)...

Cet article est une ébauche concernant l’histoire. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Couronne du Roi du Danemark Christian IV Le titre de grand-prince est un titre de noblesse, honorifiquement inférieur à celui d'empereur, mais supérieur à celui de prince souverain ou de prince royal. Ce titre est commun dans plusieurs pays d'Europe centrale, du Nord et de l'Est. [réf. souhaitée] En a...

Outer region of the volume of a star Photo taken in France during the 1999 solar eclipse The stellar atmosphere is the outer region of the volume of a star, lying above the stellar core, radiation zone and convection zone. Overview The stellar atmosphere is divided into several regions of distinct character: The photosphere, which is the atmosphere's lowest and coolest layer, is normally its only visible part.[1] Light escaping from the surface of the star stems from this region and p...

American politician Steven A. BaddourBaddour in 2008Member of the Massachusetts Senatefrom the 1st Essex districtIn office2002–2012Preceded byJames JajugaSucceeded byKathleen O'Connor Ives Personal detailsBorn1969 (age 54–55)Political partyDemocraticAlma materUniversity of Massachusetts Dartmouth, Massachusetts School of LawWebsitestevenbaddour.com 2003 official portrait Steven A. Baddour (born 1969) is an American attorney and politician from the Commonwealth of Massachusetts. H...

Japanese actor Kenichi Takitō滝藤 賢一Born (1976-11-02) November 2, 1976 (age 47)Nagoya, Aichi, JapanOccupationActorYears active1998–presentAgentAgent Office TactChildren4 Kenichi Takitō (滝藤 賢一, Takitō Ken'ichi, born November 2, 1976 in Nagoya) is a Japanese actor. Career Takitō belonged to Tatsuya Nakadai's acting academy and theater troupe Mumeijuku from 1998 to 2007.[1] Filmography Films Godzilla: Tokyo S.O.S. (2003) Climber's High (2009) – Shusaku Kan...

Branch of psychology For the academic journal, see Evolutionary Psychology (journal). Not to be confused with Evolutionary psychiatry. Part of a series onPsychology Outline History Subfields Basic psychology Abnormal Affective neuroscience Affective science Behavioral genetics Behavioral neuroscience Behaviorism Cognitive/Cognitivism Cognitive neuroscience Social Comparative Cross-cultural Cultural Developmental Differential Ecological Evolutionary Experimental Gestalt Intelligence Mathematic...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Migrasi Teuton dan Cimbri. Teuton (dari Proto-Jermanik *Þeudanōz) disebut sebagai suku Jermanik oleh pengarang Yunani dan Romawi. Menurut peta Ptolomeus, mereka tinggal di Jutland, atas persetujuan dengan Pomponius Mela.[1] Referensi ^ Northvegr - Saga Book Vol. 7 & 8. Diarsipkan dari versi asli tanggal 2...

KissI Kiss in concerto alla O2 Arena nel 2019 Paese d'origine Stati Uniti GenereHard rock[1][2][3][4]Pop metal[5][6] Periodo di attività musicale1973 – 2023 EtichettaCasablanca (1973–1982)Mercury (1982–2003)Sanctuary (2003–2008)Roadrunner-Universal (2009–2023) Album pubblicati44 Studio20 Live7 Raccolte17 Logo ufficiale Sito ufficiale Modifica dati su Wikidata · Manuale I Kiss (spesso reso graficament...

American conservationist Carole BaskinBaskin in 2019BornCarole Ann Stairs (1961-06-06) June 6, 1961 (age 62)Bexar County, Texas, U.S.Other namesCarole StairsCarole MurdockCarole LewisOccupationsAnimal sanctuary executiveanimal rights activistKnown forInvolvement in Tiger King and Dancing with the StarsTelevision Tiger King (2020–present) Dancing with the Stars (2020) Shooting Joe Exotic (2021) Spouses Michael Murdock (m. 1979; div. 199...

Academy in Worle, North Somerset, EnglandWorle Community School AcademyAddressRedwing DriveWorle, North Somerset, BS22 8XXEnglandCoordinates51°21′18″N 2°55′44″W / 51.3551°N 2.9289°W / 51.3551; -2.9289InformationTypeAcademyMottoPROUDEstablished1948Local authorityNorth SomersetTrustThe Priory Learning TrustDepartment for Education URN143137 TablesOfstedReportsPrincipalMark Tidman[1]Executive headteacherWill Roberts[1]GenderMixedAge11 to 1...

「アプリケーション」はこの項目へ転送されています。英語の意味については「wikt:応用」、「wikt:application」をご覧ください。 この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2018年4月) 古い情報を更新する必要があります。(2021年3月)出...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Main article: Timeline of the Syrian civil war vteSyrian civil war Timeline January–April 2011 May–August 2011 September–December 2011 January–April 2012 May–August 2012 September–December 2012 January–April 2013 May–December 2013 January–July 2014 August–December 2014 January–July 2015 August–December 2015 January–April 2016 May–August 2016 September–December 2016 January–April 2017 May–August 2017 September–December 2017 January–April 2018 May–August...

Logistics Management redirects here. For the magazine, see Logistics Management (magazine). For other uses, see Logistics (disambiguation). Management of the flow of resources This section may contain citations that do not verify the text. The reason given is: section – The definition of logistics lacks references so it may be inaccurate Please check for citation inaccuracies. (November 2022) (Learn how and when to remove this message) A warehouse in South Jersey, a U.S. East Coast epicente...

Islam menurut negara Afrika Aljazair Angola Benin Botswana Burkina Faso Burundi Kamerun Tanjung Verde Republik Afrika Tengah Chad Komoro Republik Demokratik Kongo Republik Kongo Djibouti Mesir Guinea Khatulistiwa Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Pantai Gading Kenya Lesotho Liberia Libya Madagaskar Malawi Mali Mauritania Mauritius Maroko Mozambik Namibia Niger Nigeria Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland Afrika Selatan ...

Sacramento KingsPallacanestro Segni distintiviUniformi di gara Casa Trasferta Terza divisa Colori socialiViola, grigio ardesia, nero[1][2] Dati societariCittàSacramento (CA) Nazione Stati Uniti CampionatoNBA ConferenceWestern Conference DivisionPacific Division Fondazione1948 DenominazioneRochester Royals (NBL)1945-1948Rochester Royals (BAA)1948-1949Rochester Royals (NBA)1949-1957Cincinnati Royals ...

Bagian dari seri tentangFasisme Inti Nasionalisme Totalitarianisme Pikiran anti-demokrasi Negara satu partai Kultus kepribadian Kediktatoran Militerisme Tindakan langsung Ekonomi campuran Kolaborasi kelas Posisi Ketiga Manusia Baru Imperialisme Tatanan sosial Topik Definisi Ekonomi Fasisme dan ideologi Fasisme dunia Simbolisme Gagasan Autarki Kolaborasi kelas Korporatisme Totalitarianisme Tokoh Benito Mussolini Adolf Hitler Francisco Franco José Antonio Primo de Rivera Corneliu Zelea Codrean...