Continued fraction closely related to the Rogers–Ramanujan identities
The Rogers–Ramanujan continued fraction is a continued fraction discovered by Rogers (1894) and independently by Srinivasa Ramanujan , and closely related to the Rogers–Ramanujan identities . It can be evaluated explicitly for a broad class of values of its argument.
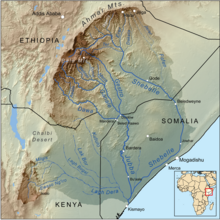
Domain coloring representation of the convergent
A
400
(
q
)
/
B
400
(
q
)
{\displaystyle A_{400}(q)/B_{400}(q)}
q
−
1
/
5
R
(
q
)
{\displaystyle q^{-1/5}R(q)}
R
(
q
)
{\displaystyle R(q)}
Definition
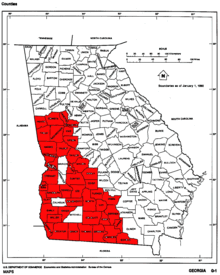
Representation of the approximation
q
1
/
5
A
400
(
q
)
/
B
400
(
q
)
{\displaystyle q^{1/5}A_{400}(q)/B_{400}(q)}
Given the functions
G
(
q
)
{\displaystyle G(q)}
H
(
q
)
{\displaystyle H(q)}
q
=
e
2
π
i
τ
{\displaystyle q=e^{2\pi i\tau }}
G
(
q
)
=
∑
n
=
0
∞
q
n
2
(
1
−
q
)
(
1
−
q
2
)
⋯
(
1
−
q
n
)
=
∑
n
=
0
∞
q
n
2
(
q
;
q
)
n
=
1
(
q
;
q
5
)
∞
(
q
4
;
q
5
)
∞
=
∏
n
=
1
∞
1
(
1
−
q
5
n
−
1
)
(
1
−
q
5
n
−
4
)
=
q
j
60
2
F
1
(
−
1
60
,
19
60
;
4
5
;
1728
j
)
=
q
(
j
−
1728
)
60
2
F
1
(
−
1
60
,
29
60
;
4
5
;
−
1728
j
−
1728
)
=
1
+
q
+
q
2
+
q
3
+
2
q
4
+
2
q
5
+
3
q
6
+
⋯
{\displaystyle {\begin{aligned}G(q)&=\sum _{n=0}^{\infty }{\frac {q^{n^{2}}}{(1-q)(1-q^{2})\cdots (1-q^{n})}}=\sum _{n=0}^{\infty }{\frac {q^{n^{2}}}{(q;q)_{n}}}={\frac {1}{(q;q^{5})_{\infty }(q^{4};q^{5})_{\infty }}}\\[6pt]&=\prod _{n=1}^{\infty }{\frac {1}{(1-q^{5n-1})(1-q^{5n-4})}}\\[6pt]&={\sqrt[{60}]{q\,j}}\,\,_{2}F_{1}\left(-{\tfrac {1}{60}},{\tfrac {19}{60}};{\tfrac {4}{5}};{\tfrac {1728}{j}}\right)\\[6pt]&={\sqrt[{60}]{q\left(j-1728\right)}}\,_{2}F_{1}\left(-{\tfrac {1}{60}},{\tfrac {29}{60}};{\tfrac {4}{5}};-{\tfrac {1728}{j-1728}}\right)\\[6pt]&=1+q+q^{2}+q^{3}+2q^{4}+2q^{5}+3q^{6}+\cdots \end{aligned}}}
and,
H
(
q
)
=
∑
n
=
0
∞
q
n
2
+
n
(
1
−
q
)
(
1
−
q
2
)
⋯
(
1
−
q
n
)
=
∑
n
=
0
∞
q
n
2
+
n
(
q
;
q
)
n
=
1
(
q
2
;
q
5
)
∞
(
q
3
;
q
5
)
∞
=
∏
n
=
1
∞
1
(
1
−
q
5
n
−
2
)
(
1
−
q
5
n
−
3
)
=
1
q
11
j
11
60
2
F
1
(
11
60
,
31
60
;
6
5
;
1728
j
)
=
1
q
11
(
j
−
1728
)
11
60
2
F
1
(
11
60
,
41
60
;
6
5
;
−
1728
j
−
1728
)
=
1
+
q
2
+
q
3
+
q
4
+
q
5
+
2
q
6
+
2
q
7
+
⋯
{\displaystyle {\begin{aligned}H(q)&=\sum _{n=0}^{\infty }{\frac {q^{n^{2}+n}}{(1-q)(1-q^{2})\cdots (1-q^{n})}}=\sum _{n=0}^{\infty }{\frac {q^{n^{2}+n}}{(q;q)_{n}}}={\frac {1}{(q^{2};q^{5})_{\infty }(q^{3};q^{5})_{\infty }}}\\[6pt]&=\prod _{n=1}^{\infty }{\frac {1}{(1-q^{5n-2})(1-q^{5n-3})}}\\[6pt]&={\frac {1}{\sqrt[{60}]{q^{11}j^{11}}}}\,_{2}F_{1}\left({\tfrac {11}{60}},{\tfrac {31}{60}};{\tfrac {6}{5}};{\tfrac {1728}{j}}\right)\\[6pt]&={\frac {1}{\sqrt[{60}]{q^{11}\left(j-1728\right)^{11}}}}\,_{2}F_{1}\left({\tfrac {11}{60}},{\tfrac {41}{60}};{\tfrac {6}{5}};-{\tfrac {1728}{j-1728}}\right)\\[6pt]&=1+q^{2}+q^{3}+q^{4}+q^{5}+2q^{6}+2q^{7}+\cdots \end{aligned}}}
with the coefficients of the q -expansion being OEIS : A003114 OEIS : A003106
(
a
;
q
)
∞
{\displaystyle (a;q)_{\infty }}
q-Pochhammer symbol , j is the j-function , and 2 F1 is the hypergeometric function . The Rogers–Ramanujan continued fraction is then
R
(
q
)
=
q
11
60
H
(
q
)
q
−
1
60
G
(
q
)
=
q
1
5
∏
n
=
1
∞
(
1
−
q
5
n
−
1
)
(
1
−
q
5
n
−
4
)
(
1
−
q
5
n
−
2
)
(
1
−
q
5
n
−
3
)
=
q
1
/
5
∏
n
=
1
∞
(
1
−
q
n
)
(
n
|
5
)
=
q
1
/
5
1
+
q
1
+
q
2
1
+
q
3
1
+
⋱
{\displaystyle {\begin{aligned}R(q)&={\frac {q^{\frac {11}{60}}H(q)}{q^{-{\frac {1}{60}}}G(q)}}=q^{\frac {1}{5}}\prod _{n=1}^{\infty }{\frac {(1-q^{5n-1})(1-q^{5n-4})}{(1-q^{5n-2})(1-q^{5n-3})}}=q^{1/5}\prod _{n=1}^{\infty }(1-q^{n})^{(n|5)}\\[8pt]&={\cfrac {q^{1/5}}{1+{\cfrac {q}{1+{\cfrac {q^{2}}{1+{\cfrac {q^{3}}{1+\ddots }}}}}}}}\end{aligned}}}
(
n
∣
m
)
{\displaystyle (n\mid m)}
One should be careful with notation since the formulas employing the j-function
j
{\displaystyle j}
q
=
e
2
π
i
τ
{\displaystyle q=e^{2\pi i\tau }}
nome ) is used throughout this section since the q -expansion of the j-function (as well as the well-known Dedekind eta function ) uses
q
=
e
2
π
i
τ
{\displaystyle q=e^{2\pi i\tau }}
nome
q
=
e
π
i
τ
{\displaystyle q=e^{\pi i\tau }}
[citation needed
Special values
If q is the nome or its square, then
q
−
1
60
G
(
q
)
{\displaystyle q^{-{\frac {1}{60}}}G(q)}
q
11
60
H
(
q
)
{\displaystyle q^{\frac {11}{60}}H(q)}
R
(
q
)
{\displaystyle R(q)}
modular functions of
τ
{\displaystyle \tau }
complex multiplication implies that their values for
τ
{\displaystyle \tau }
algebraic numbers that can be evaluated explicitly.
Given the general form where Ramanujan used the nome
q
=
e
π
i
τ
{\displaystyle q=e^{\pi i\tau }}
R
(
q
)
=
q
1
/
5
1
+
q
1
+
q
2
1
+
q
3
1
+
⋱
{\displaystyle R(q)={\cfrac {q^{1/5}}{1+{\cfrac {q}{1+{\cfrac {q^{2}}{1+{\cfrac {q^{3}}{1+\ddots }}}}}}}}}
f
when
τ
=
i
{\displaystyle \tau =i}
R
(
e
−
π
)
=
e
−
π
5
1
+
e
−
π
1
+
e
−
2
π
1
+
⋱
=
1
2
φ
(
5
−
φ
3
/
2
)
(
5
4
+
φ
3
/
2
)
=
0.511428
…
{\displaystyle R{\big (}e^{-\pi }{\big )}={\cfrac {e^{-{\frac {\pi }{5}}}}{1+{\cfrac {e^{-\pi }}{1+{\cfrac {e^{-2\pi }}{1+\ddots }}}}}}={\tfrac {1}{2}}\varphi \,({\sqrt {5}}-\varphi ^{3/2})({\sqrt[{4}]{5}}+\varphi ^{3/2})=0.511428\dots }
when
τ
=
2
i
{\displaystyle \tau =2i}
R
(
e
−
2
π
)
=
e
−
2
π
5
1
+
e
−
2
π
1
+
e
−
4
π
1
+
⋱
=
5
4
φ
1
/
2
−
φ
=
0.284079
…
{\displaystyle R{\big (}e^{-2\pi }{\big )}={\cfrac {e^{-{\frac {2\pi }{5}}}}{1+{\cfrac {e^{-2\pi }}{1+{\cfrac {e^{-4\pi }}{1+\ddots }}}}}}={{\sqrt[{4}]{5}}\,\varphi ^{1/2}-\varphi }=0.284079\dots }
when
τ
=
4
i
{\displaystyle \tau =4i}
R
(
e
−
4
π
)
=
e
−
4
π
5
1
+
e
−
4
π
1
+
e
−
8
π
1
+
⋱
=
1
2
φ
(
5
−
φ
3
/
2
)
(
−
5
4
+
φ
3
/
2
)
=
0.081002
…
{\displaystyle R{\big (}e^{-4\pi }{\big )}={\cfrac {e^{-{\frac {4\pi }{5}}}}{1+{\cfrac {e^{-4\pi }}{1+{\cfrac {e^{-8\pi }}{1+\ddots }}}}}}={\tfrac {1}{2}}\varphi \,({\sqrt {5}}-\varphi ^{3/2})(-{\sqrt[{4}]{5}}+\varphi ^{3/2})=0.081002\dots }
when
τ
=
2
5
i
{\displaystyle \tau =2{\sqrt {5}}i}
R
(
e
−
2
5
π
)
=
e
−
2
π
5
1
+
e
−
2
π
5
1
+
e
−
4
π
5
1
+
⋱
=
5
1
+
(
5
3
/
4
(
φ
−
1
)
5
/
2
−
1
)
1
/
5
−
φ
=
0.0602094
…
{\displaystyle R{\big (}e^{-2{\sqrt {5}}\pi }{\big )}={\cfrac {e^{-{\frac {2\pi }{\sqrt {5}}}}}{1+{\cfrac {e^{-2\pi {\sqrt {5}}}}{1+{\cfrac {e^{-4\pi {\sqrt {5}}}}{1+\ddots }}}}}}={\frac {\sqrt {5}}{1+{\big (}5^{3/4}(\varphi -1)^{5/2}-1{\big )}^{1/5}}}-\varphi =0.0602094\dots }
when
τ
=
5
i
{\displaystyle \tau =5i}
R
(
e
−
5
π
)
=
e
−
π
1
+
e
−
5
π
1
+
e
−
10
π
1
+
⋱
=
1
+
φ
2
φ
+
(
1
2
(
4
−
φ
−
3
φ
−
1
)
(
3
φ
3
/
2
−
5
4
)
)
1
/
5
−
φ
=
0.0432139
…
{\displaystyle R{\big (}e^{-5\pi }{\big )}={\cfrac {e^{-\pi }}{1+{\cfrac {e^{-5\pi }}{1+{\cfrac {e^{-10\pi }}{1+\ddots }}}}}}={\frac {1+\varphi ^{2}}{\varphi +{\big (}{\frac {1}{2}}(4-\varphi -3{\sqrt {\varphi -1}})(3\varphi ^{3/2}-{\sqrt[{4}]{5}}){\big )}^{1/5}}}-\varphi =0.0432139\dots }
when
τ
=
10
i
{\displaystyle \tau =10i}
R
(
e
−
10
π
)
=
e
−
2
π
1
+
e
−
10
π
1
+
e
−
20
π
1
+
⋱
=
1
+
φ
2
φ
+
(
3
1
+
φ
2
−
4
−
φ
)
1
/
5
−
φ
=
0.00186744
…
{\displaystyle R{\big (}e^{-10\pi }{\big )}={\cfrac {e^{-2\pi }}{1+{\cfrac {e^{-10\pi }}{1+{\cfrac {e^{-20\pi }}{1+\ddots }}}}}}={\frac {1+\varphi ^{2}}{\varphi +{\big (}3{\sqrt {1+\varphi ^{2}}}-4-\varphi {\big )}^{1/5}}}-\varphi =0.00186744\dots }
when
τ
=
20
i
{\displaystyle \tau =20i}
R
(
e
−
20
π
)
=
e
−
4
π
1
+
e
−
20
π
1
+
e
−
40
π
1
+
⋱
=
1
+
φ
2
φ
+
(
1
2
(
4
−
φ
−
3
φ
−
1
)
(
3
φ
3
/
2
+
5
4
)
)
1
/
5
−
φ
=
0.00000348734
…
{\displaystyle R{\big (}e^{-20\pi }{\big )}={\cfrac {e^{-4\pi }}{1+{\cfrac {e^{-20\pi }}{1+{\cfrac {e^{-40\pi }}{1+\ddots }}}}}}={\frac {1+\varphi ^{2}}{\varphi +{\big (}{\frac {1}{2}}(4-\varphi -3{\sqrt {\varphi -1}})(3\varphi ^{3/2}+{\sqrt[{4}]{5}}){\big )}^{1/5}}}-\varphi =0.00000348734\dots }
and
φ
=
1
+
5
2
{\displaystyle \varphi ={\tfrac {1+{\sqrt {5}}}{2}}}
golden ratio . Note that
R
(
e
−
2
π
)
{\displaystyle R{\big (}e^{-2\pi }{\big )}}
quartic equation ,
x
4
+
2
x
3
−
6
x
2
−
2
x
+
1
=
0
{\displaystyle x^{4}+2x^{3}-6x^{2}-2x+1=0}
while
R
(
e
−
π
)
{\displaystyle R{\big (}e^{-\pi }{\big )}}
R
(
e
−
4
π
)
{\displaystyle R{\big (}e^{-4\pi }{\big )}}
octic ,
y
4
+
2
φ
4
y
3
+
6
φ
2
y
2
−
2
φ
4
y
+
1
=
0
{\displaystyle y^{4}+2\varphi ^{4}y^{3}+6\varphi ^{2}y^{2}-2\varphi ^{4}y+1=0}
(since
φ
{\displaystyle \varphi }
integer m , then
R
(
e
−
2
π
/
m
)
{\displaystyle R(e^{-2\pi /m})}
R
(
e
−
2
π
m
)
{\displaystyle R(e^{-2\pi \,m})}
[
R
(
e
−
2
π
/
m
)
+
φ
]
[
R
(
e
−
2
π
m
)
+
φ
]
=
5
φ
{\displaystyle {\bigl [}R(e^{-2\pi /m})+\varphi {\bigr ]}{\bigl [}R(e^{-2\pi \,m})+\varphi {\bigr ]}={\sqrt {5}}\,\varphi }
The algebraic degree k of
R
(
e
−
π
n
)
{\displaystyle R(e^{-\pi \,n})}
n
=
1
,
2
,
3
,
4
,
…
{\displaystyle n=1,2,3,4,\dots }
k
=
8
,
4
,
32
,
8
,
…
{\displaystyle k=8,4,32,8,\dots }
OEIS : A082682
Incidentally, these continued fractions can be used to solve some quintic equations as shown in a later section.
G (q ) and H (q )Interestingly, there are explicit formulas for
G
(
q
)
{\displaystyle G(q)}
H
(
q
)
{\displaystyle H(q)}
j-function
j
(
τ
)
{\displaystyle j(\tau )}
R
(
q
)
{\displaystyle R(q)}
j
(
τ
)
{\displaystyle j(\tau )}
q
=
e
2
π
i
τ
{\displaystyle q=e^{2\pi \,i\tau }}
j
(
τ
)
,
G
(
q
)
,
H
(
q
)
{\displaystyle j(\tau ),\,G(q),\,H(q)}
r
=
R
(
q
)
{\displaystyle r=R(q)}
q
{\displaystyle q}
G
(
q
)
=
∏
n
=
1
∞
1
(
1
−
q
5
n
−
1
)
(
1
−
q
5
n
−
4
)
=
q
1
/
60
j
(
τ
)
1
/
60
(
r
20
−
228
r
15
+
494
r
10
+
228
r
5
+
1
)
1
/
20
{\displaystyle {\begin{aligned}G(q)&=\prod _{n=1}^{\infty }{\frac {1}{(1-q^{5n-1})(1-q^{5n-4})}}\\[6pt]&=q^{1/60}{\frac {j(\tau )^{1/60}}{(r^{20}-228r^{15}+494r^{10}+228r^{5}+1)^{1/20}}}\end{aligned}}}
H
(
q
)
=
∏
n
=
1
∞
1
(
1
−
q
5
n
−
2
)
(
1
−
q
5
n
−
3
)
=
−
1
q
11
/
60
(
r
20
−
228
r
15
+
494
r
10
+
228
r
5
+
1
)
11
/
20
j
(
τ
)
11
/
60
(
r
10
+
11
r
5
−
1
)
{\displaystyle {\begin{aligned}H(q)&=\prod _{n=1}^{\infty }{\frac {1}{(1-q^{5n-2})(1-q^{5n-3})}}\\[6pt]&={\frac {-1}{q^{11/60}}}{\frac {(r^{20}-228r^{15}+494r^{10}+228r^{5}+1)^{11/20}}{j(\tau )^{11/60}\,(r^{10}+11r^{5}-1)}}\end{aligned}}}
Of course, the secondary formulas imply that
q
−
1
/
60
G
(
q
)
{\displaystyle q^{-1/60}G(q)}
q
11
/
60
H
(
q
)
{\displaystyle q^{11/60}H(q)}
algebraic numbers (though normally of high degree) for
τ
{\displaystyle \tau }
imaginary quadratic field . For example, the formulas above simplify to,
G
(
e
−
2
π
)
=
(
e
−
2
π
)
1
/
60
1
(
5
φ
)
1
/
4
1
R
(
e
−
2
π
)
=
1.00187093
…
H
(
e
−
2
π
)
=
1
(
e
−
2
π
)
11
/
60
1
(
5
φ
)
1
/
4
R
(
e
−
2
π
)
=
1.00000349
…
{\displaystyle {\begin{aligned}G(e^{-2\pi })&=(e^{-2\pi })^{1/60}{\frac {1}{(5\,\varphi )^{1/4}}}{\frac {1}{\sqrt {R(e^{-2\pi })}}}\\[6pt]&=1.00187093\dots \\[6pt]H(e^{-2\pi })&={\frac {1}{(e^{-2\pi })^{11/60}}}{\frac {1}{(5\,\varphi )^{1/4}}}{\sqrt {R(e^{-2\pi })}}\\[6pt]&=1.00000349\ldots \end{aligned}}}
and,
G
(
e
−
4
π
)
=
(
e
−
4
π
)
1
/
60
1
(
5
φ
3
)
1
/
4
(
φ
+
5
4
)
1
/
4
1
R
(
e
−
4
π
)
=
1.000003487354
…
H
(
e
−
4
π
)
=
1
(
e
−
4
π
)
11
/
60
1
(
5
φ
3
)
1
/
4
(
φ
+
5
4
)
1
/
4
R
(
e
−
4
π
)
=
1.000000000012
…
{\displaystyle {\begin{aligned}G(e^{-4\pi })&=(e^{-4\pi })^{1/60}{\frac {1}{(5\,\varphi ^{3})^{1/4}\,(\varphi +{\sqrt[{4}]{5}})^{1/4}}}{\frac {1}{\sqrt {R(e^{-4\pi })}}}\\[6pt]&=1.000003487354\dots \\[6pt]H(e^{-4\pi })&={\frac {1}{(e^{-4\pi })^{11/60}}}{\frac {1}{(5\,\varphi ^{3})^{1/4}\,(\varphi +{\sqrt[{4}]{5}})^{1/4}}}{\sqrt {R(e^{-4\pi })}}\\[6pt]&=1.000000000012\dots \end{aligned}}}
and so on, with
φ
{\displaystyle \varphi }
Derivation of special values
Tangential sums
In the following we express the essential theorems of the Rogers-Ramanujan continued fractions R and S by using the tangential sums and tangential differences:
a
⊕
b
=
tan
[
arctan
(
a
)
+
arctan
(
b
)
]
=
a
+
b
1
−
a
b
{\displaystyle a\oplus b=\tan {\bigl [}\arctan(a)+\arctan(b){\bigr ]}={\frac {a+b}{1-ab}}}
c
⊖
d
=
tan
[
arctan
(
c
)
−
arctan
(
d
)
]
=
c
−
d
1
+
c
d
{\displaystyle c\ominus d=\tan {\bigl [}\arctan(c)-\arctan(d){\bigr ]}={\frac {c-d}{1+cd}}}
The elliptic nome and the complementary nome have this relationship to each other:
ln
(
q
)
ln
(
q
1
)
=
π
2
{\displaystyle \ln(q)\ln(q_{1})=\pi ^{2}}
The complementary nome of a modulus k is equal to the nome of the Pythagorean complementary modulus:
q
1
(
k
)
=
q
(
k
′
)
=
q
(
1
−
k
2
)
{\displaystyle q_{1}(k)=q(k')=q({\sqrt {1-k^{2}}})}
These are the reflection theorems for the continued fractions R and S:
S
(
q
)
⊕
S
(
q
1
)
=
Φ
{\displaystyle S(q)\oplus S(q_{1})=\Phi }
R
(
q
2
)
⊕
R
(
q
1
2
)
=
Φ
−
1
{\displaystyle R(q^{2})\oplus R(q_{1}^{2})=\Phi ^{-1}}
The letter
Φ
{\displaystyle \Phi }
Golden number exactly:
Φ
=
1
2
(
5
+
1
)
=
cot
[
1
2
arctan
(
2
)
]
=
2
cos
(
1
5
π
)
{\displaystyle \Phi ={\tfrac {1}{2}}({\sqrt {5}}+1)=\cot[{\tfrac {1}{2}}\arctan(2)]=2\cos({\tfrac {1}{5}}{\pi })}
Φ
−
1
=
1
2
(
5
−
1
)
=
tan
[
1
2
arctan
(
2
)
]
=
2
sin
(
1
10
π
)
{\displaystyle \Phi ^{-1}={\tfrac {1}{2}}({\sqrt {5}}-1)=\tan[{\tfrac {1}{2}}\arctan(2)]=2\sin({\tfrac {1}{10}}{\pi })}
The theorems for the squared nome are constructed as follows:
R
(
q
)
2
R
(
q
2
)
−
1
⊕
R
(
q
)
R
(
q
2
)
2
=
1
{\displaystyle R(q)^{2}R(q^{2})^{-1}\oplus R(q)R(q^{2})^{2}=1}
S
(
q
)
2
R
(
q
2
)
−
1
⊖
S
(
q
)
R
(
q
2
)
2
=
1
{\displaystyle S(q)^{2}R(q^{2})^{-1}\ominus S(q)R(q^{2})^{2}=1}
Following relations between the continued fractions and the Jacobi theta functions are given:
S
(
q
)
⊕
R
(
q
2
)
=
ϑ
00
(
q
1
/
5
)
2
−
ϑ
00
(
q
)
2
5
ϑ
00
(
q
5
)
2
−
ϑ
00
(
q
)
2
{\displaystyle S(q)\oplus R(q^{2})={\frac {\vartheta _{00}(q^{1/5})^{2}-\vartheta _{00}(q)^{2}}{5\,\vartheta _{00}(q^{5})^{2}-\vartheta _{00}(q)^{2}}}}
R
(
q
)
⊖
R
(
q
2
)
=
ϑ
01
(
q
)
2
−
ϑ
01
(
q
1
/
5
)
2
5
ϑ
01
(
q
5
)
2
−
ϑ
01
(
q
)
2
{\displaystyle R(q)\ominus R(q^{2})={\frac {\vartheta _{01}(q)^{2}-\vartheta _{01}(q^{1/5})^{2}}{5\,\vartheta _{01}(q^{5})^{2}-\vartheta _{01}(q)^{2}}}}
Derivation of Lemniscatic values
Into the now shown theorems certain values are inserted:
S
[
exp
(
−
π
)
]
⊕
S
[
exp
(
−
π
)
]
=
Φ
{\displaystyle S{\bigl [}\exp(-\pi ){\bigr ]}\oplus S{\bigl [}\exp(-\pi ){\bigr ]}=\Phi }
Therefore following identity is valid:
S
[
exp
(
−
π
)
]
=
tan
[
1
2
arctan
(
Φ
)
]
=
tan
[
1
4
π
−
1
4
arctan
(
2
)
]
{\displaystyle S{\bigl [}\exp(-\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{2}}\arctan(\Phi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\arctan(2){\bigr ]}}
In an analogue pattern we get this result:
R
[
exp
(
−
2
π
)
]
⊕
R
[
exp
(
−
2
π
)
]
=
Φ
−
1
{\displaystyle R{\bigl [}\exp(-2\pi ){\bigr ]}\oplus R{\bigl [}\exp(-2\pi ){\bigr ]}=\Phi ^{-1}}
Therefore following identity is valid:
R
[
exp
(
−
2
π
)
]
=
tan
[
1
2
arctan
(
Φ
−
1
)
]
=
tan
[
1
4
arctan
(
2
)
]
{\displaystyle R{\bigl [}\exp(-2\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{2}}\arctan(\Phi ^{-1}){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\arctan(2){\bigr ]}}
Furthermore we get the same relation by using the above mentioned theorem about the Jacobi theta functions:
S
[
exp
(
−
π
)
]
⊕
R
[
exp
(
−
2
π
)
]
=
S
(
q
)
⊕
R
(
q
2
)
[
q
=
exp
(
−
π
)
]
=
{\displaystyle S{\bigl [}\exp(-\pi ){\bigr ]}\oplus R{\bigl [}\exp(-2\pi ){\bigr ]}=S(q)\oplus R(q^{2}){\bigl [}q=\exp(-\pi ){\bigr ]}=}
=
ϑ
00
(
q
1
/
5
)
2
−
ϑ
00
(
q
)
2
5
ϑ
00
(
q
5
)
2
−
ϑ
00
(
q
)
2
[
q
=
exp
(
−
π
)
]
=
1
{\displaystyle ={\frac {\vartheta _{00}(q^{1/5})^{2}-\vartheta _{00}(q)^{2}}{5\,\vartheta _{00}(q^{5})^{2}-\vartheta _{00}(q)^{2}}}{\bigl [}q=\exp(-\pi ){\bigr ]}=1}
This result appears because of the Poisson summation formula and this equation can be solved in this way:
R
[
exp
(
−
2
π
)
]
=
1
⊖
S
[
exp
(
−
π
)
]
=
1
⊖
tan
[
1
4
π
−
1
4
arctan
(
2
)
]
=
tan
[
1
4
arctan
(
2
)
]
{\displaystyle R{\bigl [}\exp(-2\pi ){\bigr ]}=1\ominus S{\bigl [}\exp(-\pi ){\bigr ]}=1\ominus \tan {\bigl [}{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\arctan(2){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\arctan(2){\bigr ]}}
By taking the other mentioned theorem about the Jacobi theta functions a next value can be determined:
R
[
exp
(
−
π
)
]
⊖
R
[
exp
(
−
2
π
)
]
=
R
(
q
)
⊖
R
(
q
2
)
[
q
=
exp
(
−
π
)
]
=
{\displaystyle R{\bigl [}\exp(-\pi ){\bigr ]}\ominus R{\bigl [}\exp(-2\pi ){\bigr ]}=R(q)\ominus R(q^{2}){\bigl [}q=\exp(-\pi ){\bigr ]}=}
=
ϑ
01
(
q
)
2
−
ϑ
01
(
q
1
/
5
)
2
5
ϑ
01
(
q
5
)
2
−
ϑ
01
(
q
)
2
[
q
=
exp
(
−
π
)
]
=
5
4
−
1
5
4
+
1
=
5
4
⊖
1
=
tan
[
arctan
(
5
4
)
−
1
4
π
]
{\displaystyle ={\frac {\vartheta _{01}(q)^{2}-\vartheta _{01}(q^{1/5})^{2}}{5\,\vartheta _{01}(q^{5})^{2}-\vartheta _{01}(q)^{2}}}{\bigl [}q=\exp(-\pi ){\bigr ]}={\frac {{\sqrt[{4}]{5}}-1}{{\sqrt[{4}]{5}}+1}}={\sqrt[{4}]{5}}\ominus 1=\tan {\bigl [}\arctan({\sqrt[{4}]{5}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}
That equation chain leads to this tangential sum:
R
[
exp
(
−
π
)
]
=
R
[
exp
(
−
2
π
)
]
⊕
tan
[
arctan
(
5
4
)
−
1
4
π
]
{\displaystyle R{\bigl [}\exp(-\pi ){\bigr ]}=R{\bigl [}\exp(-2\pi ){\bigr ]}\oplus \tan {\bigl [}\arctan({\sqrt[{4}]{5}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}
And therefore following result appears:
R
[
exp
(
−
π
)
]
=
tan
[
1
4
arctan
(
2
)
+
arctan
(
5
4
)
−
1
4
π
]
{\displaystyle R{\bigl [}\exp(-\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\arctan(2)+\arctan({\sqrt[{4}]{5}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}
In the next step we use the reflection theorem for the continued fraction R again:
R
[
exp
(
−
π
)
]
⊕
R
[
exp
(
−
4
π
)
]
=
Φ
−
1
{\displaystyle R{\bigl [}\exp(-\pi ){\bigr ]}\oplus R{\bigl [}\exp(-4\pi ){\bigr ]}=\Phi ^{-1}}
R
[
exp
(
−
4
π
)
]
=
tan
[
1
2
arctan
(
2
)
]
⊖
R
[
exp
(
−
π
)
]
{\displaystyle R{\bigl [}\exp(-4\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{2}}\arctan(2){\bigr ]}\ominus R{\bigl [}\exp(-\pi ){\bigr ]}}
And a further result appears:
R
[
exp
(
−
4
π
)
]
=
tan
[
1
4
arctan
(
2
)
−
arctan
(
5
4
)
+
1
4
π
]
{\displaystyle R{\bigl [}\exp(-4\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\arctan(2)-\arctan({\sqrt[{4}]{5}}\,)+{\tfrac {1}{4}}\pi {\bigr ]}}
Derivation of Non-Lemniscatic values
The reflection theorem is now used for following values:
R
[
exp
(
−
2
π
)
]
⊕
R
[
exp
(
−
2
2
π
)
]
=
Φ
−
1
{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}\oplus R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}=\Phi ^{-1}}
The Jacobi theta theorem leads to a further relation:
R
[
exp
(
−
2
π
)
]
⊖
R
[
exp
(
−
2
2
π
)
]
=
R
(
q
)
⊖
R
(
q
2
)
[
q
=
exp
(
−
2
π
)
]
=
{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}\ominus R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}=R(q)\ominus R(q^{2}){\bigl [}q=\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=}
=
ϑ
01
(
q
)
2
−
ϑ
01
(
q
1
/
5
)
2
5
ϑ
01
(
q
5
)
2
−
ϑ
01
(
q
)
2
[
q
=
exp
(
−
2
π
)
]
=
tan
[
2
arctan
(
1
3
5
−
1
3
6
30
+
4
5
3
+
1
3
6
30
−
4
5
3
)
−
1
4
π
]
{\displaystyle ={\frac {\vartheta _{01}(q)^{2}-\vartheta _{01}(q^{1/5})^{2}}{5\,\vartheta _{01}(q^{5})^{2}-\vartheta _{01}(q)^{2}}}{\bigl [}q=\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=\tan {\bigl [}2\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}
By tangential adding the now mentioned two theorems we get this result:
R
[
exp
(
−
2
π
)
]
⊕
R
[
exp
(
−
2
π
)
]
=
Φ
−
1
⊕
tan
[
2
arctan
(
1
3
5
−
1
3
6
30
+
4
5
3
+
1
3
6
30
−
4
5
3
)
−
1
4
π
]
{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}\oplus R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=\Phi ^{-1}\oplus \tan {\bigl [}2\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}
R
[
exp
(
−
2
π
)
]
=
tan
[
arctan
(
1
3
5
−
1
3
6
30
+
4
5
3
+
1
3
6
30
−
4
5
3
)
−
1
4
arccot
(
2
)
]
{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=\tan {\bigl [}\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,)-{\tfrac {1}{4}}\operatorname {arccot}(2){\bigr ]}}
By tangential substraction that result appears:
R
[
exp
(
−
2
2
π
)
]
⊕
R
[
exp
(
−
2
2
π
)
]
=
Φ
−
1
⊖
tan
[
2
arctan
(
1
3
5
−
1
3
6
30
+
4
5
3
+
1
3
6
30
−
4
5
3
)
−
1
4
π
]
{\displaystyle R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}\oplus R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}=\Phi ^{-1}\ominus \tan {\bigl [}2\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}
R
[
exp
(
−
2
2
π
)
]
=
tan
[
1
4
arccot
(
−
2
)
−
arctan
(
1
3
5
−
1
3
6
30
+
4
5
3
+
1
3
6
30
−
4
5
3
)
]
{\displaystyle R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\operatorname {arccot}(-2)-\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,){\bigr ]}}
In an alternative solution way we use the theorem for the squared nome:
R
[
exp
(
−
2
π
)
]
2
R
[
exp
(
−
2
2
π
)
]
−
1
⊕
R
[
exp
(
−
2
π
)
]
R
[
exp
(
−
2
2
π
)
]
2
=
1
{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{2}R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}^{-1}\oplus R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}^{2}=1}
{
R
[
exp
(
−
2
π
)
]
2
R
[
exp
(
−
2
2
π
)
]
−
1
+
1
}
{
R
[
exp
(
−
2
π
)
]
R
[
exp
(
−
2
2
π
)
]
2
+
1
}
=
2
{\displaystyle {\bigl \{}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{2}R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}^{-1}+1{\bigr \}}{\bigl \{}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}^{2}+1{\bigr \}}=2}
Now the reflection theorem is taken again:
R
[
exp
(
−
2
2
π
)
]
=
Φ
−
1
⊖
R
[
exp
(
−
2
π
)
]
{\displaystyle R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}=\Phi ^{-1}\ominus R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}}
R
[
exp
(
−
2
2
π
)
]
=
1
−
Φ
R
[
exp
(
−
2
π
)
]
Φ
+
R
[
exp
(
−
2
π
)
]
{\displaystyle R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}={\frac {1-\Phi R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}}{\Phi +R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}}}}
The insertion of the last mentioned expression into the squared nome theorem gives that equation:
{
R
[
exp
(
−
2
π
)
]
2
Φ
+
R
[
exp
(
−
2
π
)
]
1
−
Φ
R
[
exp
(
−
2
π
)
]
+
1
}
⟨
R
[
exp
(
−
2
π
)
]
{
1
−
Φ
R
[
exp
(
−
2
π
)
]
}
2
{
Φ
+
R
[
exp
(
−
2
π
)
]
}
2
+
1
⟩
=
2
{\displaystyle {\biggl \{}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{2}{\frac {\Phi +R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}}{1-\Phi R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}}}+1{\biggr \}}{\biggl \langle }R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}{\frac {{\bigl \{}1-\Phi R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}{\bigr \}}^{2}}{{\bigl \{}\Phi +R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}{\bigr \}}^{2}}}+1{\biggr \rangle }=2}
Erasing the denominators gives an equation of sixth degree:
R
[
exp
(
−
2
π
)
]
6
+
2
Φ
−
2
R
[
exp
(
−
2
π
)
]
5
−
5
Φ
−
1
R
[
exp
(
−
2
π
)
]
4
+
{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{6}+2\,\Phi ^{-2}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{5}-{\sqrt {5}}\,\Phi ^{-1}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{4}+}
+
2
5
Φ
R
[
exp
(
−
2
π
)
]
3
+
5
Φ
−
1
R
[
exp
(
−
2
π
)
]
2
+
2
Φ
−
2
R
[
exp
(
−
2
π
)
]
−
1
=
0
{\displaystyle +2\,{\sqrt {5}}\,\Phi R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{3}+{\sqrt {5}}\,\Phi ^{-1}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{2}+2\,\Phi ^{-2}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}-1=0}
The solution of this equation is the already mentioned solution:
R
[
exp
(
−
2
π
)
]
=
tan
[
arctan
(
1
3
5
−
1
3
6
30
+
4
5
3
+
1
3
6
30
−
4
5
3
)
−
1
4
arccot
(
2
)
]
{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=\tan {\bigl [}\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,)-{\tfrac {1}{4}}\operatorname {arccot}(2){\bigr ]}}
R
(
q
)
{\displaystyle R(q)}
Dedekind eta function , a modular form of weight 1/2, as,[ 1]
1
R
(
q
)
−
R
(
q
)
=
η
(
τ
5
)
η
(
5
τ
)
+
1
{\displaystyle {\frac {1}{R(q)}}-R(q)={\frac {\eta ({\frac {\tau }{5}})}{\eta (5\tau )}}+1}
1
R
5
(
q
)
−
R
5
(
q
)
=
[
η
(
τ
)
η
(
5
τ
)
]
6
+
11
{\displaystyle {\frac {1}{R^{5}(q)}}-R^{5}(q)=\left[{\frac {\eta (\tau )}{\eta (5\tau )}}\right]^{6}+11}
The Rogers-Ramanujan continued fraction can also be expressed in terms of the Jacobi theta functions . Recall the notation,
ϑ
10
(
0
;
τ
)
=
θ
2
(
q
)
=
∑
n
=
−
∞
∞
q
(
n
+
1
/
2
)
2
ϑ
00
(
0
;
τ
)
=
θ
3
(
q
)
=
∑
n
=
−
∞
∞
q
n
2
ϑ
01
(
0
;
τ
)
=
θ
4
(
q
)
=
∑
n
=
−
∞
∞
(
−
1
)
n
q
n
2
{\displaystyle {\begin{aligned}\vartheta _{10}(0;\tau )&=\theta _{2}(q)=\sum _{n=-\infty }^{\infty }q^{(n+1/2)^{2}}\\\vartheta _{00}(0;\tau )&=\theta _{3}(q)=\sum _{n=-\infty }^{\infty }q^{n^{2}}\\\vartheta _{01}(0;\tau )&=\theta _{4}(q)=\sum _{n=-\infty }^{\infty }(-1)^{n}q^{n^{2}}\end{aligned}}}
The notation
θ
n
{\displaystyle \theta _{n}}
θ
2
4
+
θ
4
4
=
θ
3
4
{\displaystyle \theta _{2}^{4}+\theta _{4}^{4}=\theta _{3}^{4}}
R
(
x
)
=
tan
{
1
2
arccot
[
1
2
+
θ
4
(
x
1
/
5
)
[
5
θ
4
(
x
5
)
2
−
θ
4
(
x
)
2
]
2
θ
4
(
x
5
)
[
θ
4
(
x
)
2
−
θ
4
(
x
1
/
5
)
2
]
]
}
{\displaystyle R(x)=\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}+{\frac {\theta _{4}(x^{1/5})[5\,\theta _{4}(x^{5})^{2}-\theta _{4}(x)^{2}]}{2\,\theta _{4}(x^{5})[\theta _{4}(x)^{2}-\theta _{4}(x^{1/5})^{2}]}}{\biggr ]}{\biggr \}}}
R
(
x
)
=
tan
{
1
2
arccot
[
1
2
+
(
θ
2
(
x
1
/
10
)
θ
3
(
x
1
/
10
)
θ
4
(
x
1
/
10
)
2
3
θ
2
(
x
5
/
2
)
θ
3
(
x
5
/
2
)
θ
4
(
x
5
/
2
)
)
1
/
3
]
}
{\displaystyle R(x)=\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}+{\bigg (}{\frac {\theta _{2}(x^{1/10})\,\theta _{3}(x^{1/10})\,\theta _{4}(x^{1/10})}{2^{3}\,\theta _{2}(x^{5/2})\,\theta _{3}(x^{5/2})\,\theta _{4}(x^{5/2})}}{\bigg )}^{1/3}{\biggr ]}{\biggr \}}}
R
(
x
)
=
tan
{
1
2
arctan
[
1
2
−
θ
4
(
x
)
2
2
θ
4
(
x
5
)
2
]
}
1
/
5
×
tan
{
1
2
arccot
[
1
2
−
θ
4
(
x
)
2
2
θ
4
(
x
5
)
2
]
}
2
/
5
{\displaystyle R(x)=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(x)^{2}}{2\,\theta _{4}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}\times \tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(x)^{2}}{2\,\theta _{4}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}}
R
(
x
)
=
tan
{
1
2
arctan
[
1
2
−
θ
4
(
x
1
/
2
)
2
2
θ
4
(
x
5
/
2
)
2
]
}
2
/
5
×
cot
{
1
2
arccot
[
1
2
−
θ
4
(
x
1
/
2
)
2
2
θ
4
(
x
5
/
2
)
2
]
}
1
/
5
{\displaystyle R(x)=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(x^{1/2})^{2}}{2\,\theta _{4}(x^{5/2})^{2}}}{\biggr ]}{\biggr \}}^{2/5}\times \cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(x^{1/2})^{2}}{2\,\theta _{4}(x^{5/2})^{2}}}{\biggr ]}{\biggr \}}^{1/5}}
Note, however, that theta functions normally use the nome q = e iπτ Dedekind eta function uses the square of the nome q = e 2iπτ x has been employed instead to maintain consistency between all functions. For example, let
τ
=
−
1
{\displaystyle \tau ={\sqrt {-1}}}
x
=
e
−
π
{\displaystyle x=e^{-\pi }}
R (x ) formulas which is the correct evaluation of the continued fraction given previously,
R
(
e
−
π
)
=
1
2
φ
(
5
−
φ
3
/
2
)
(
5
4
+
φ
3
/
2
)
=
0.511428
…
{\displaystyle R{\big (}e^{-\pi }{\big )}={\frac {1}{2}}\varphi \,({\sqrt {5}}-\varphi ^{3/2})({\sqrt[{4}]{5}}+\varphi ^{3/2})=0.511428\dots }
One can also define the elliptic nome ,
q
(
k
)
=
exp
[
−
π
K
(
1
−
k
2
)
/
K
(
k
)
]
{\displaystyle q(k)=\exp {\big [}-\pi K({\sqrt {1-k^{2}}})/K(k){\big ]}}
The small letter k describes the elliptic modulus and the big letter K describes the complete elliptic integral of the first kind. The continued fraction can then be also expressed by the Jacobi elliptic functions as follows:
R
(
q
(
k
)
)
=
tan
{
1
2
arctan
y
}
1
/
5
tan
{
1
2
arccot
y
}
2
/
5
=
{
y
2
+
1
−
1
y
}
1
/
5
{
y
[
1
y
2
+
1
−
1
]
}
2
/
5
{\displaystyle R{\big (}q(k){\big )}=\tan {\biggl \{}{\frac {1}{2}}\arctan y{\biggr \}}^{1/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} y{\biggr \}}^{2/5}=\left\{{\frac {{\sqrt {y^{2}+1}}-1}{y}}\right\}^{1/5}\left\{y\left[{\sqrt {{\frac {1}{y^{2}}}+1}}-1\right]\right\}^{2/5}}
with
y
=
2
k
2
sn
[
2
5
K
(
k
)
;
k
]
2
sn
[
4
5
K
(
k
)
;
k
]
2
5
−
k
2
sn
[
2
5
K
(
k
)
;
k
]
2
sn
[
4
5
K
(
k
)
;
k
]
2
.
{\displaystyle y={\frac {2k^{2}\,{\text{sn}}[{\tfrac {2}{5}}K(k);k]^{2}\,{\text{sn}}[{\tfrac {4}{5}}K(k);k]^{2}}{5-k^{2}\,{\text{sn}}[{\tfrac {2}{5}}K(k);k]^{2}\,{\text{sn}}[{\tfrac {4}{5}}K(k);k]^{2}}}.}
Relation to j-function
One formula involving the j-function and the Dedekind eta function is this:
j
(
τ
)
=
(
x
2
+
10
x
+
5
)
3
x
{\displaystyle j(\tau )={\frac {(x^{2}+10x+5)^{3}}{x}}}
where
x
=
[
5
η
(
5
τ
)
η
(
τ
)
]
6
.
{\displaystyle x=\left[{\frac {{\sqrt {5}}\,\eta (5\tau )}{\eta (\tau )}}\right]^{6}.\,}
1
R
5
(
q
)
−
R
5
(
q
)
=
[
η
(
τ
)
η
(
5
τ
)
]
6
+
11
{\displaystyle {\frac {1}{R^{5}(q)}}-R^{5}(q)=\left[{\frac {\eta (\tau )}{\eta (5\tau )}}\right]^{6}+11}
Eliminating the eta quotient
x
{\displaystyle x}
j (τ ) in terms of
r
=
R
(
q
)
{\displaystyle r=R(q)}
j
(
τ
)
=
−
(
r
20
−
228
r
15
+
494
r
10
+
228
r
5
+
1
)
3
r
5
(
r
10
+
11
r
5
−
1
)
5
j
(
τ
)
−
1728
=
−
(
r
30
+
522
r
25
−
10005
r
20
−
10005
r
10
−
522
r
5
+
1
)
2
r
5
(
r
10
+
11
r
5
−
1
)
5
{\displaystyle {\begin{aligned}&j(\tau )=-{\frac {(r^{20}-228r^{15}+494r^{10}+228r^{5}+1)^{3}}{r^{5}(r^{10}+11r^{5}-1)^{5}}}\\[6pt]&j(\tau )-1728=-{\frac {(r^{30}+522r^{25}-10005r^{20}-10005r^{10}-522r^{5}+1)^{2}}{r^{5}(r^{10}+11r^{5}-1)^{5}}}\end{aligned}}}
where the numerator and denominator are polynomial invariants of the icosahedron . Using the modular equation between
R
(
q
)
{\displaystyle R(q)}
R
(
q
5
)
{\displaystyle R(q^{5})}
j
(
5
τ
)
=
−
(
r
20
+
12
r
15
+
14
r
10
−
12
r
5
+
1
)
3
r
25
(
r
10
+
11
r
5
−
1
)
j
(
5
τ
)
−
1728
=
−
(
r
30
+
18
r
25
+
75
r
20
+
75
r
10
−
18
r
5
+
1
)
2
r
25
(
r
10
+
11
r
5
−
1
)
{\displaystyle {\begin{aligned}&j(5\tau )=-{\frac {(r^{20}+12r^{15}+14r^{10}-12r^{5}+1)^{3}}{r^{25}(r^{10}+11r^{5}-1)}}\\[6pt]&j(5\tau )-1728=-{\frac {(r^{30}+18r^{25}+75r^{20}+75r^{10}-18r^{5}+1)^{2}}{r^{25}(r^{10}+11r^{5}-1)}}\end{aligned}}}
Let
z
=
r
5
−
1
r
5
{\displaystyle z=r^{5}-{\frac {1}{r^{5}}}}
j
(
5
τ
)
=
−
(
z
2
+
12
z
+
16
)
3
z
+
11
{\displaystyle j(5\tau )=-{\frac {\left(z^{2}+12z+16\right)^{3}}{z+11}}}
where
z
∞
=
−
[
5
η
(
25
τ
)
η
(
5
τ
)
]
6
−
11
,
z
0
=
−
[
η
(
τ
)
η
(
5
τ
)
]
6
−
11
,
z
1
=
[
η
(
5
τ
+
2
5
)
η
(
5
τ
)
]
6
−
11
,
z
2
=
−
[
η
(
5
τ
+
4
5
)
η
(
5
τ
)
]
6
−
11
,
z
3
=
[
η
(
5
τ
+
6
5
)
η
(
5
τ
)
]
6
−
11
,
z
4
=
−
[
η
(
5
τ
+
8
5
)
η
(
5
τ
)
]
6
−
11
{\displaystyle {\begin{aligned}&z_{\infty }=-\left[{\frac {{\sqrt {5}}\,\eta (25\tau )}{\eta (5\tau )}}\right]^{6}-11,\ z_{0}=-\left[{\frac {\eta (\tau )}{\eta (5\tau )}}\right]^{6}-11,\ z_{1}=\left[{\frac {\eta ({\frac {5\tau +2}{5}})}{\eta (5\tau )}}\right]^{6}-11,\\[6pt]&z_{2}=-\left[{\frac {\eta ({\frac {5\tau +4}{5}})}{\eta (5\tau )}}\right]^{6}-11,\ z_{3}=\left[{\frac {\eta ({\frac {5\tau +6}{5}})}{\eta (5\tau )}}\right]^{6}-11,\ z_{4}=-\left[{\frac {\eta ({\frac {5\tau +8}{5}})}{\eta (5\tau )}}\right]^{6}-11\end{aligned}}}
which in fact is the j-invariant of the elliptic curve ,
y
2
+
(
1
+
r
5
)
x
y
+
r
5
y
=
x
3
+
r
5
x
2
{\displaystyle y^{2}+(1+r^{5})xy+r^{5}y=x^{3}+r^{5}x^{2}}
parameterized by the non-cusp points of the modular curve
X
1
(
5
)
{\displaystyle X_{1}(5)}
Functional equation
For convenience, one can also use the notation
r
(
τ
)
=
R
(
q
)
{\displaystyle r(\tau )=R(q)}
q = e2πiτ . While other modular functions like the j-invariant satisfies,
j
(
−
1
τ
)
=
j
(
τ
)
{\displaystyle j(-{\tfrac {1}{\tau }})=j(\tau )}
and the Dedekind eta function has,
η
(
−
1
τ
)
=
−
i
τ
η
(
τ
)
{\displaystyle \eta (-{\tfrac {1}{\tau }})={\sqrt {-i\tau }}\,\eta (\tau )}
the functional equation of the Rogers–Ramanujan continued fraction involves[ 2] golden ratio
φ
{\displaystyle \varphi }
r
(
−
1
τ
)
=
1
−
φ
r
(
τ
)
φ
+
r
(
τ
)
{\displaystyle r(-{\tfrac {1}{\tau }})={\frac {1-\varphi \,r(\tau )}{\varphi +r(\tau )}}}
Incidentally,
r
(
7
+
i
10
)
=
i
{\displaystyle r({\tfrac {7+i}{10}})=i}
Modular equations
There are modular equations between
R
(
q
)
{\displaystyle R(q)}
R
(
q
n
)
{\displaystyle R(q^{n})}
prime n are as follows.[ 3]
For
n
=
2
{\displaystyle n=2}
u
=
R
(
q
)
{\displaystyle u=R(q)}
v
=
R
(
q
2
)
{\displaystyle v=R(q^{2})}
v
−
u
2
=
(
v
+
u
2
)
u
v
2
.
{\displaystyle v-u^{2}=(v+u^{2})uv^{2}.}
n
=
3
{\displaystyle n=3}
u
=
R
(
q
)
{\displaystyle u=R(q)}
v
=
R
(
q
3
)
{\displaystyle v=R(q^{3})}
(
v
−
u
3
)
(
1
+
u
v
3
)
=
3
u
2
v
2
.
{\displaystyle (v-u^{3})(1+uv^{3})=3u^{2}v^{2}.}
n
=
5
{\displaystyle n=5}
u
=
R
(
q
)
{\displaystyle u=R(q)}
v
=
R
(
q
5
)
{\displaystyle v=R(q^{5})}
v
(
v
4
−
3
v
3
+
4
v
2
−
2
v
+
1
)
=
(
v
4
+
2
v
3
+
4
v
2
+
3
v
+
1
)
u
5
.
{\displaystyle v(v^{4}-3v^{3}+4v^{2}-2v+1)=(v^{4}+2v^{3}+4v^{2}+3v+1)u^{5}.}
n
=
5
{\displaystyle n=5}
u
=
R
(
q
)
{\displaystyle u=R(q)}
v
=
R
(
q
5
)
{\displaystyle v=R(q^{5})}
φ
=
1
+
5
2
{\displaystyle \varphi ={\tfrac {1+{\sqrt {5}}}{2}}}
u
5
=
v
(
v
2
−
φ
2
v
+
φ
2
)
(
v
2
−
φ
−
2
v
+
φ
−
2
)
(
v
2
+
v
+
φ
2
)
(
v
2
+
v
+
φ
−
2
)
.
{\displaystyle u^{5}={\frac {v\,(v^{2}-\varphi ^{2}v+\varphi ^{2})(v^{2}-\varphi ^{-2}v+\varphi ^{-2})}{(v^{2}+v+\varphi ^{2})(v^{2}+v+\varphi ^{-2})}}.}
n
=
11
{\displaystyle n=11}
u
=
R
(
q
)
{\displaystyle u=R(q)}
v
=
R
(
q
11
)
{\displaystyle v=R(q^{11})}
u
v
(
u
10
+
11
u
5
−
1
)
(
v
10
+
11
v
5
−
1
)
=
(
u
−
v
)
12
.
{\displaystyle uv(u^{10}+11u^{5}-1)(v^{10}+11v^{5}-1)=(u-v)^{12}.}
n
=
5
{\displaystyle n=5}
v
10
+
11
v
5
−
1
=
(
v
2
+
v
−
1
)
(
v
4
−
3
v
3
+
4
v
2
−
2
v
+
1
)
(
v
4
+
2
v
3
+
4
v
2
+
3
v
+
1
)
.
{\displaystyle v^{10}+11v^{5}-1=(v^{2}+v-1)(v^{4}-3v^{3}+4v^{2}-2v+1)(v^{4}+2v^{3}+4v^{2}+3v+1).}
Other results
Ramanujan found many other interesting results regarding
R
(
q
)
{\displaystyle R(q)}
[ 4]
a
,
b
∈
R
+
{\displaystyle a,b\in \mathbb {R} ^{+}}
φ
{\displaystyle \varphi }
golden ratio .
If
a
b
=
π
2
{\displaystyle ab=\pi ^{2}}
[
R
(
e
−
2
a
)
+
φ
]
[
R
(
e
−
2
b
)
+
φ
]
=
5
φ
.
{\displaystyle {\bigl [}R(e^{-2a})+\varphi {\bigl ]}{\bigl [}R(e^{-2b})+\varphi {\bigr ]}={\sqrt {5}}\,\varphi .}
If
5
a
b
=
π
2
{\displaystyle 5ab=\pi ^{2}}
[
R
5
(
e
−
2
a
)
+
φ
5
]
[
R
5
(
e
−
2
b
)
+
φ
5
]
=
5
5
φ
5
.
{\displaystyle {\bigl [}R^{5}(e^{-2a})+\varphi ^{5}{\bigl ]}{\bigl [}R^{5}(e^{-2b})+\varphi ^{5}{\bigr ]}=5{\sqrt {5}}\,\varphi ^{5}.}
The powers of
R
(
q
)
{\displaystyle R(q)}
cube ,
R
3
(
q
)
=
α
β
{\displaystyle R^{3}(q)={\frac {\alpha }{\beta }}}
where
α
=
∑
n
=
0
∞
q
2
n
1
−
q
5
n
+
2
−
∑
n
=
0
∞
q
3
n
+
1
1
−
q
5
n
+
3
,
{\displaystyle \alpha =\sum _{n=0}^{\infty }{\frac {q^{2n}}{1-q^{5n+2}}}-\sum _{n=0}^{\infty }{\frac {q^{3n+1}}{1-q^{5n+3}}},}
β
=
∑
n
=
0
∞
q
n
1
−
q
5
n
+
1
−
∑
n
=
0
∞
q
4
n
+
3
1
−
q
5
n
+
4
.
{\displaystyle \beta =\sum _{n=0}^{\infty }{\frac {q^{n}}{1-q^{5n+1}}}-\sum _{n=0}^{\infty }{\frac {q^{4n+3}}{1-q^{5n+4}}}.}
For its fifth power, let
w
=
R
(
q
)
R
2
(
q
2
)
{\displaystyle w=R(q)R^{2}(q^{2})}
R
5
(
q
)
=
w
(
1
−
w
1
+
w
)
2
,
R
5
(
q
2
)
=
w
2
(
1
+
w
1
−
w
)
{\displaystyle R^{5}(q)=w\left({\frac {1-w}{1+w}}\right)^{2},\;\;R^{5}(q^{2})=w^{2}\left({\frac {1+w}{1-w}}\right)}
Quintic equations
The general quintic equation in Bring-Jerrard form:
x
5
−
5
x
−
4
a
=
0
{\displaystyle x^{5}-5x-4a=0}
for every real value
a
>
1
{\displaystyle a>1}
R
(
q
)
{\displaystyle R(q)}
q
(
k
)
=
exp
[
−
π
K
(
1
−
k
2
)
/
K
(
k
)
]
.
{\displaystyle q(k)=\exp {\big [}-\pi K({\sqrt {1-k^{2}}})/K(k){\big ]}.}
To solve this quintic, the elliptic modulus must first be determined as
k
=
tan
[
1
4
π
−
1
4
arccsc
(
a
2
)
]
.
{\displaystyle k=\tan[{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\operatorname {arccsc}(a^{2})].}
Then the real solution is
x
=
2
−
{
1
−
R
[
q
(
k
)
]
}
{
1
+
R
[
q
(
k
)
2
]
}
R
[
q
(
k
)
]
R
[
q
(
k
)
2
]
4
cot
⟨
4
arctan
{
S
}
⟩
−
3
4
=
2
−
{
1
−
R
[
q
(
k
)
]
}
{
1
+
R
[
q
(
k
)
2
]
}
R
[
q
(
k
)
]
R
[
q
(
k
)
2
]
2
S
−
1
+
2
S
+
1
+
1
S
−
S
−
3
4
.
{\displaystyle {\begin{aligned}x&={\frac {2-{\bigl \{}1-R[q(k)]{\bigr \}}{\bigl \{}1+R[q(k)^{2}]{\bigr \}}}{{\sqrt {R[q(k)]\,R[q(k)^{2}]}}\,{\sqrt[{4}]{4\cot \langle 4\arctan\{S\}\rangle -3}}}}\\&={\frac {2-{\bigl \{}1-R[q(k)]{\bigr \}}{\bigl \{}1+R[q(k)^{2}]{\bigr \}}}{{\sqrt {R[q(k)]R[q(k)^{2}]}}\,{\sqrt[{4}]{{\frac {2}{S-1}}+{\frac {2}{S+1}}+{\frac {1}{S}}-S-3}}}}.\end{aligned}}}
where
S
=
R
[
q
(
k
)
]
R
2
[
q
(
k
)
2
]
.
{\displaystyle S=R[q(k)]\,R^{2}[q(k)^{2}].}
R
(
q
)
{\displaystyle R(q)}
S
{\displaystyle S}
R
5
[
q
(
k
)
]
=
S
(
1
−
S
1
+
S
)
2
{\displaystyle R^{5}[q(k)]=S\left({\frac {1-S}{1+S}}\right)^{2}}
Example 1
x
5
−
x
−
1
=
0
{\displaystyle x^{5}-x-1=0}
Transform to,
(
5
4
x
)
5
−
5
(
5
4
x
)
−
4
(
5
4
5
4
)
=
0
{\displaystyle ({\sqrt[{4}]{5}}x)^{5}-5({\sqrt[{4}]{5}}x)-4({\tfrac {5}{4}}{\sqrt[{4}]{5}})=0}
thus,
a
=
5
4
5
4
{\displaystyle a={\tfrac {5}{4}}{\sqrt[{4}]{5}}}
k
=
tan
[
1
4
π
−
1
4
arccsc
(
a
2
)
]
=
5
5
/
4
+
25
5
−
16
5
5
/
4
+
25
5
+
16
{\displaystyle k=\tan[{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\operatorname {arccsc}(a^{2})]={\tfrac {5^{5/4}+{\sqrt {25{\sqrt {5}}-16}}}{5^{5/4}+{\sqrt {25{\sqrt {5}}+16}}}}}
q
(
k
)
=
0.0851414716
…
{\displaystyle q(k)=0.0851414716\dots }
R
[
q
(
k
)
]
=
0.5633613184
…
{\displaystyle R[q(k)]=0.5633613184\dots }
R
[
q
(
k
)
2
]
=
0.3706122329
…
{\displaystyle R[q(k)^{2}]=0.3706122329\dots }
and the solution is:
x
=
2
−
{
1
−
R
[
q
(
k
)
]
}
{
1
+
R
[
q
(
k
)
2
]
}
R
[
q
(
k
)
]
R
[
q
(
k
)
2
]
20
cot
⟨
4
arctan
{
R
[
q
(
k
)
]
R
[
q
(
k
)
2
]
2
}
⟩
−
15
4
=
1.167303978
…
{\displaystyle x={\frac {2-{\bigl \{}1-R[q(k)]{\bigr \}}{\bigl \{}1+R[q(k)^{2}]{\bigr \}}}{{\sqrt {R[q(k)]\,R[q(k)^{2}]}}\,{\sqrt[{4}]{20\cot \langle 4\arctan\{R[q(k)]\,R[q(k)^{2}]^{2}\}\rangle -15}}}}=1.167303978\dots }
and can not be represented by elementary root expressions.
Example 2
x
5
−
5
x
−
4
(
81
32
4
)
=
0
{\displaystyle x^{5}-5x-4{\Bigl (}{\sqrt[{4}]{\tfrac {81}{32}}}{\Bigr )}=0}
thus,
a
=
81
32
4
{\displaystyle a={\sqrt[{4}]{\tfrac {81}{32}}}}
Given the more familiar continued fractions with closed-forms,
r
1
=
R
(
e
−
π
)
=
1
2
φ
(
5
−
φ
3
/
2
)
(
5
4
+
φ
3
/
2
)
=
0.511428
…
{\displaystyle r_{1}=R{\big (}e^{-\pi }{\big )}={\tfrac {1}{2}}\varphi \,({\sqrt {5}}-\varphi ^{3/2})({\sqrt[{4}]{5}}+\varphi ^{3/2})=0.511428\dots }
r
2
=
R
(
e
−
2
π
)
=
5
4
φ
1
/
2
−
φ
=
0.284079
…
{\displaystyle r_{2}=R{\big (}e^{-2\pi }{\big )}={\sqrt[{4}]{5}}\,\varphi ^{1/2}-\varphi =0.284079\dots }
r
4
=
R
(
e
−
4
π
)
=
1
2
φ
(
5
−
φ
3
/
2
)
(
−
5
4
+
φ
3
/
2
)
=
0.081002
…
{\displaystyle r_{4}=R{\big (}e^{-4\pi }{\big )}={\tfrac {1}{2}}\varphi \,({\sqrt {5}}-\varphi ^{3/2})(-{\sqrt[{4}]{5}}+\varphi ^{3/2})=0.081002\dots }
with golden ratio
φ
=
1
+
5
2
{\displaystyle \varphi ={\tfrac {1+{\sqrt {5}}}{2}}}
x
=
5
4
2
−
{
1
−
r
1
}
{
1
+
r
2
}
r
1
r
2
20
cot
⟨
4
arctan
{
r
1
r
2
2
}
⟩
−
15
4
=
5
4
2
−
{
1
−
r
2
}
{
1
+
r
4
}
r
2
r
4
20
cot
⟨
4
arctan
{
r
2
r
4
2
}
⟩
−
15
4
=
8
4
=
1.681792
…
{\displaystyle {\begin{aligned}x&={\sqrt[{4}]{5}}\,{\frac {2-{\bigl \{}1-r_{1}{\bigr \}}{\bigl \{}1+r_{2}{\bigr \}}}{{\sqrt {r_{1}\,r_{2}}}\,{\sqrt[{4}]{20\cot \langle 4\arctan\{r_{1}\,r_{2}^{2}\}\rangle -15}}}}\\[6pt]&={\sqrt[{4}]{5}}\,{\frac {2-{\bigl \{}1-r_{2}{\bigr \}}{\bigl \{}1+r_{4}{\bigr \}}}{{\sqrt {r_{2}\,r_{4}}}\,{\sqrt[{4}]{20\cot \langle 4\arctan\{r_{2}\,r_{4}^{2}\}\rangle -15}}}}\\[6pt]&={\sqrt[{4}]{8}}=1.681792\dots \end{aligned}}}
References
Rogers, L. J. (1894), "Second Memoir on the Expansion of certain Infinite Products" , Proc. London Math. Soc. , s1-25 (1): 318–343, doi :10.1112/plms/s1-25.1.318 Berndt, B. C.; Chan, H. H.; Huang, S. S.; Kang, S. Y.; Sohn, J.; Son, S. H. (1999), "The Rogers–Ramanujan continued fraction" (PDF) , Journal of Computational and Applied Mathematics , 105 (1–2): 9–24, doi :10.1016/S0377-0427(99)00033-3
External links


























![{\displaystyle {\begin{aligned}G(q)&=\sum _{n=0}^{\infty }{\frac {q^{n^{2}}}{(1-q)(1-q^{2})\cdots (1-q^{n})}}=\sum _{n=0}^{\infty }{\frac {q^{n^{2}}}{(q;q)_{n}}}={\frac {1}{(q;q^{5})_{\infty }(q^{4};q^{5})_{\infty }}}\\[6pt]&=\prod _{n=1}^{\infty }{\frac {1}{(1-q^{5n-1})(1-q^{5n-4})}}\\[6pt]&={\sqrt[{60}]{q\,j}}\,\,_{2}F_{1}\left(-{\tfrac {1}{60}},{\tfrac {19}{60}};{\tfrac {4}{5}};{\tfrac {1728}{j}}\right)\\[6pt]&={\sqrt[{60}]{q\left(j-1728\right)}}\,_{2}F_{1}\left(-{\tfrac {1}{60}},{\tfrac {29}{60}};{\tfrac {4}{5}};-{\tfrac {1728}{j-1728}}\right)\\[6pt]&=1+q+q^{2}+q^{3}+2q^{4}+2q^{5}+3q^{6}+\cdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17f340bf6668c9c9d6b2ba43139d7d57edb2897d)
![{\displaystyle {\begin{aligned}H(q)&=\sum _{n=0}^{\infty }{\frac {q^{n^{2}+n}}{(1-q)(1-q^{2})\cdots (1-q^{n})}}=\sum _{n=0}^{\infty }{\frac {q^{n^{2}+n}}{(q;q)_{n}}}={\frac {1}{(q^{2};q^{5})_{\infty }(q^{3};q^{5})_{\infty }}}\\[6pt]&=\prod _{n=1}^{\infty }{\frac {1}{(1-q^{5n-2})(1-q^{5n-3})}}\\[6pt]&={\frac {1}{\sqrt[{60}]{q^{11}j^{11}}}}\,_{2}F_{1}\left({\tfrac {11}{60}},{\tfrac {31}{60}};{\tfrac {6}{5}};{\tfrac {1728}{j}}\right)\\[6pt]&={\frac {1}{\sqrt[{60}]{q^{11}\left(j-1728\right)^{11}}}}\,_{2}F_{1}\left({\tfrac {11}{60}},{\tfrac {41}{60}};{\tfrac {6}{5}};-{\tfrac {1728}{j-1728}}\right)\\[6pt]&=1+q^{2}+q^{3}+q^{4}+q^{5}+2q^{6}+2q^{7}+\cdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87587e00106bca786494f3e62ce429384f4c2798)

![{\displaystyle {\begin{aligned}R(q)&={\frac {q^{\frac {11}{60}}H(q)}{q^{-{\frac {1}{60}}}G(q)}}=q^{\frac {1}{5}}\prod _{n=1}^{\infty }{\frac {(1-q^{5n-1})(1-q^{5n-4})}{(1-q^{5n-2})(1-q^{5n-3})}}=q^{1/5}\prod _{n=1}^{\infty }(1-q^{n})^{(n|5)}\\[8pt]&={\cfrac {q^{1/5}}{1+{\cfrac {q}{1+{\cfrac {q^{2}}{1+{\cfrac {q^{3}}{1+\ddots }}}}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc22e435ee365200f68b711f8c6d5b535f315c11)








![{\displaystyle R{\big (}e^{-\pi }{\big )}={\cfrac {e^{-{\frac {\pi }{5}}}}{1+{\cfrac {e^{-\pi }}{1+{\cfrac {e^{-2\pi }}{1+\ddots }}}}}}={\tfrac {1}{2}}\varphi \,({\sqrt {5}}-\varphi ^{3/2})({\sqrt[{4}]{5}}+\varphi ^{3/2})=0.511428\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a6c3405e7c30139be9ebc5883957bbe2961a640)

![{\displaystyle R{\big (}e^{-2\pi }{\big )}={\cfrac {e^{-{\frac {2\pi }{5}}}}{1+{\cfrac {e^{-2\pi }}{1+{\cfrac {e^{-4\pi }}{1+\ddots }}}}}}={{\sqrt[{4}]{5}}\,\varphi ^{1/2}-\varphi }=0.284079\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf153ea27c1bdc48270a3aca1ea339ba0bde25c6)

![{\displaystyle R{\big (}e^{-4\pi }{\big )}={\cfrac {e^{-{\frac {4\pi }{5}}}}{1+{\cfrac {e^{-4\pi }}{1+{\cfrac {e^{-8\pi }}{1+\ddots }}}}}}={\tfrac {1}{2}}\varphi \,({\sqrt {5}}-\varphi ^{3/2})(-{\sqrt[{4}]{5}}+\varphi ^{3/2})=0.081002\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc99d55aaf5b1eb8d359179bc54934e150593ca2)



![{\displaystyle R{\big (}e^{-5\pi }{\big )}={\cfrac {e^{-\pi }}{1+{\cfrac {e^{-5\pi }}{1+{\cfrac {e^{-10\pi }}{1+\ddots }}}}}}={\frac {1+\varphi ^{2}}{\varphi +{\big (}{\frac {1}{2}}(4-\varphi -3{\sqrt {\varphi -1}})(3\varphi ^{3/2}-{\sqrt[{4}]{5}}){\big )}^{1/5}}}-\varphi =0.0432139\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/60a554a375df6c825bfa296bad44ad31f95f29c0)



![{\displaystyle R{\big (}e^{-20\pi }{\big )}={\cfrac {e^{-4\pi }}{1+{\cfrac {e^{-20\pi }}{1+{\cfrac {e^{-40\pi }}{1+\ddots }}}}}}={\frac {1+\varphi ^{2}}{\varphi +{\big (}{\frac {1}{2}}(4-\varphi -3{\sqrt {\varphi -1}})(3\varphi ^{3/2}+{\sqrt[{4}]{5}}){\big )}^{1/5}}}-\varphi =0.00000348734\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c901757a378f5272b59181c76b14ea2cec9f96b)









![{\displaystyle {\bigl [}R(e^{-2\pi /m})+\varphi {\bigr ]}{\bigl [}R(e^{-2\pi \,m})+\varphi {\bigr ]}={\sqrt {5}}\,\varphi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bd65a5de209ee413c11f16d48c302e2aaa695f4)








![{\displaystyle {\begin{aligned}G(q)&=\prod _{n=1}^{\infty }{\frac {1}{(1-q^{5n-1})(1-q^{5n-4})}}\\[6pt]&=q^{1/60}{\frac {j(\tau )^{1/60}}{(r^{20}-228r^{15}+494r^{10}+228r^{5}+1)^{1/20}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bed060d9273df8e5ead63436a909dc5fdbb403f)
![{\displaystyle {\begin{aligned}H(q)&=\prod _{n=1}^{\infty }{\frac {1}{(1-q^{5n-2})(1-q^{5n-3})}}\\[6pt]&={\frac {-1}{q^{11/60}}}{\frac {(r^{20}-228r^{15}+494r^{10}+228r^{5}+1)^{11/20}}{j(\tau )^{11/60}\,(r^{10}+11r^{5}-1)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36323b5de18a9b28b21f3eea8bad32bd6979b040)


![{\displaystyle {\begin{aligned}G(e^{-2\pi })&=(e^{-2\pi })^{1/60}{\frac {1}{(5\,\varphi )^{1/4}}}{\frac {1}{\sqrt {R(e^{-2\pi })}}}\\[6pt]&=1.00187093\dots \\[6pt]H(e^{-2\pi })&={\frac {1}{(e^{-2\pi })^{11/60}}}{\frac {1}{(5\,\varphi )^{1/4}}}{\sqrt {R(e^{-2\pi })}}\\[6pt]&=1.00000349\ldots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0540a9b2d189ce12385c3a3eabc99832d16b8e64)
![{\displaystyle {\begin{aligned}G(e^{-4\pi })&=(e^{-4\pi })^{1/60}{\frac {1}{(5\,\varphi ^{3})^{1/4}\,(\varphi +{\sqrt[{4}]{5}})^{1/4}}}{\frac {1}{\sqrt {R(e^{-4\pi })}}}\\[6pt]&=1.000003487354\dots \\[6pt]H(e^{-4\pi })&={\frac {1}{(e^{-4\pi })^{11/60}}}{\frac {1}{(5\,\varphi ^{3})^{1/4}\,(\varphi +{\sqrt[{4}]{5}})^{1/4}}}{\sqrt {R(e^{-4\pi })}}\\[6pt]&=1.000000000012\dots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/415d12f61351a318ce5cb5565f6a3c56f62b5d0a)
![{\displaystyle a\oplus b=\tan {\bigl [}\arctan(a)+\arctan(b){\bigr ]}={\frac {a+b}{1-ab}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4694eeba504d3db4a4c2a1812403bfc3e17f836)
![{\displaystyle c\ominus d=\tan {\bigl [}\arctan(c)-\arctan(d){\bigr ]}={\frac {c-d}{1+cd}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebd5804fe87d111f63768e8f219419efa7725e57)





![{\displaystyle \Phi ={\tfrac {1}{2}}({\sqrt {5}}+1)=\cot[{\tfrac {1}{2}}\arctan(2)]=2\cos({\tfrac {1}{5}}{\pi })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00cd707c883f6a33b179764fe529673a685d30b0)
![{\displaystyle \Phi ^{-1}={\tfrac {1}{2}}({\sqrt {5}}-1)=\tan[{\tfrac {1}{2}}\arctan(2)]=2\sin({\tfrac {1}{10}}{\pi })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00e6aa1506dfff4cd10059114065f1a571130e1b)




![{\displaystyle S{\bigl [}\exp(-\pi ){\bigr ]}\oplus S{\bigl [}\exp(-\pi ){\bigr ]}=\Phi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d39217aba6ce97c57822a0a8fedf5d7726728d9)
![{\displaystyle S{\bigl [}\exp(-\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{2}}\arctan(\Phi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\arctan(2){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/831e2ef305caed1a334de327f6af3d1900904c01)
![{\displaystyle R{\bigl [}\exp(-2\pi ){\bigr ]}\oplus R{\bigl [}\exp(-2\pi ){\bigr ]}=\Phi ^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90ab593a1f3d5e881102454dbf15a36e72afc0e3)
![{\displaystyle R{\bigl [}\exp(-2\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{2}}\arctan(\Phi ^{-1}){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\arctan(2){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16b4fbcf1342b7623fe6bf2f115e18ea9022fcc4)
![{\displaystyle S{\bigl [}\exp(-\pi ){\bigr ]}\oplus R{\bigl [}\exp(-2\pi ){\bigr ]}=S(q)\oplus R(q^{2}){\bigl [}q=\exp(-\pi ){\bigr ]}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/178cde333a5b70c5ff7fbb710e602e594d66d44a)
![{\displaystyle ={\frac {\vartheta _{00}(q^{1/5})^{2}-\vartheta _{00}(q)^{2}}{5\,\vartheta _{00}(q^{5})^{2}-\vartheta _{00}(q)^{2}}}{\bigl [}q=\exp(-\pi ){\bigr ]}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fd833ed5fb7e5980d12a76241e496b9d5a7bd1b)
![{\displaystyle R{\bigl [}\exp(-2\pi ){\bigr ]}=1\ominus S{\bigl [}\exp(-\pi ){\bigr ]}=1\ominus \tan {\bigl [}{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\arctan(2){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\arctan(2){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93961e24edfe705f24ead2bf290ca4ed5e79f7bb)
![{\displaystyle R{\bigl [}\exp(-\pi ){\bigr ]}\ominus R{\bigl [}\exp(-2\pi ){\bigr ]}=R(q)\ominus R(q^{2}){\bigl [}q=\exp(-\pi ){\bigr ]}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/467dc496e6b3529dd86f63acea4f98ecb42beec9)
![{\displaystyle ={\frac {\vartheta _{01}(q)^{2}-\vartheta _{01}(q^{1/5})^{2}}{5\,\vartheta _{01}(q^{5})^{2}-\vartheta _{01}(q)^{2}}}{\bigl [}q=\exp(-\pi ){\bigr ]}={\frac {{\sqrt[{4}]{5}}-1}{{\sqrt[{4}]{5}}+1}}={\sqrt[{4}]{5}}\ominus 1=\tan {\bigl [}\arctan({\sqrt[{4}]{5}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcf199a4e70a3743b61131ea9c2118de3aee91fd)
![{\displaystyle R{\bigl [}\exp(-\pi ){\bigr ]}=R{\bigl [}\exp(-2\pi ){\bigr ]}\oplus \tan {\bigl [}\arctan({\sqrt[{4}]{5}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bdb2ba5fd90f09aee88032cf729907f49c8a548)
![{\displaystyle R{\bigl [}\exp(-\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\arctan(2)+\arctan({\sqrt[{4}]{5}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f68aaca63a16f3c39356479b18765ddf8bfec76)
![{\displaystyle R{\bigl [}\exp(-\pi ){\bigr ]}\oplus R{\bigl [}\exp(-4\pi ){\bigr ]}=\Phi ^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbb4d5e961fad8c6ce68dba48f8fe696b384eef4)
![{\displaystyle R{\bigl [}\exp(-4\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{2}}\arctan(2){\bigr ]}\ominus R{\bigl [}\exp(-\pi ){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62349fa9ff32f7b0d2070a35ba39e36e07ef9d8d)
![{\displaystyle R{\bigl [}\exp(-4\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\arctan(2)-\arctan({\sqrt[{4}]{5}}\,)+{\tfrac {1}{4}}\pi {\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11ea8662f257c4d713f0cf4fff430113ab1f96c2)
![{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}\oplus R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}=\Phi ^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9d8fbc08bb4a3a852a23c7a9e1214ac28d30941)
![{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}\ominus R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}=R(q)\ominus R(q^{2}){\bigl [}q=\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/039f770796d02ff14157dcb5ab2c7ef5c7a500bd)
![{\displaystyle ={\frac {\vartheta _{01}(q)^{2}-\vartheta _{01}(q^{1/5})^{2}}{5\,\vartheta _{01}(q^{5})^{2}-\vartheta _{01}(q)^{2}}}{\bigl [}q=\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=\tan {\bigl [}2\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6225f8ac541e8bdc2e7cb17ae1798dd21bba046f)
![{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}\oplus R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=\Phi ^{-1}\oplus \tan {\bigl [}2\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6abdeb36fe2008a02304892182a7645670d38557)
![{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=\tan {\bigl [}\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,)-{\tfrac {1}{4}}\operatorname {arccot}(2){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d1ba43a88aafaece47de397366208a98b53304d)
![{\displaystyle R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}\oplus R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}=\Phi ^{-1}\ominus \tan {\bigl [}2\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,)-{\tfrac {1}{4}}\pi {\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc072e8da9259e662e23173f6da154478d0fd633)
![{\displaystyle R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}=\tan {\bigl [}{\tfrac {1}{4}}\operatorname {arccot}(-2)-\arctan({\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}\,){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/704965a10a1a13ddb8f0fdff4ed1620eef0c9069)
![{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{2}R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}^{-1}\oplus R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}^{2}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21afb95996f9d394404603afcc761735ad3fad2b)
![{\displaystyle {\bigl \{}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{2}R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}^{-1}+1{\bigr \}}{\bigl \{}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}^{2}+1{\bigr \}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f8fd7359989247d309f916d5070b83508ca0b57)
![{\displaystyle R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}=\Phi ^{-1}\ominus R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83cecbb4dec7aa95cc6c182f11623fdb86060cde)
![{\displaystyle R{\bigl [}\exp(-2{\sqrt {2}}\,\pi ){\bigr ]}={\frac {1-\Phi R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}}{\Phi +R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cac30d6d5d5bf53533d3bc573c7b69a547912fa2)
![{\displaystyle {\biggl \{}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{2}{\frac {\Phi +R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}}{1-\Phi R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}}}+1{\biggr \}}{\biggl \langle }R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}{\frac {{\bigl \{}1-\Phi R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}{\bigr \}}^{2}}{{\bigl \{}\Phi +R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}{\bigr \}}^{2}}}+1{\biggr \rangle }=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d00ea266326bcdbb8873cfc054be0e6653478012)
![{\displaystyle R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{6}+2\,\Phi ^{-2}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{5}-{\sqrt {5}}\,\Phi ^{-1}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{4}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8970c3dd6242ae8dee9d39d0ff593b54c69c90b7)
![{\displaystyle +2\,{\sqrt {5}}\,\Phi R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{3}+{\sqrt {5}}\,\Phi ^{-1}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}^{2}+2\,\Phi ^{-2}R{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}-1=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8e9e08500522cf65d470bbaa6ff78cc728d9428)

![{\displaystyle {\frac {1}{R^{5}(q)}}-R^{5}(q)=\left[{\frac {\eta (\tau )}{\eta (5\tau )}}\right]^{6}+11}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bd161c8522f2d0446ee11792d6f37d8f8aeb7d5)



![{\displaystyle R(x)=\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}+{\frac {\theta _{4}(x^{1/5})[5\,\theta _{4}(x^{5})^{2}-\theta _{4}(x)^{2}]}{2\,\theta _{4}(x^{5})[\theta _{4}(x)^{2}-\theta _{4}(x^{1/5})^{2}]}}{\biggr ]}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc53eb3cb13875f9bf0ecc132c54d61e4ced3610)
![{\displaystyle R(x)=\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}+{\bigg (}{\frac {\theta _{2}(x^{1/10})\,\theta _{3}(x^{1/10})\,\theta _{4}(x^{1/10})}{2^{3}\,\theta _{2}(x^{5/2})\,\theta _{3}(x^{5/2})\,\theta _{4}(x^{5/2})}}{\bigg )}^{1/3}{\biggr ]}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/357426562078839bb726ac261902f089fe6e47a4)
![{\displaystyle R(x)=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(x)^{2}}{2\,\theta _{4}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}\times \tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(x)^{2}}{2\,\theta _{4}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18d0dec82ce02b84a41c35ae5d0eb624c7b85a8)
![{\displaystyle R(x)=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(x^{1/2})^{2}}{2\,\theta _{4}(x^{5/2})^{2}}}{\biggr ]}{\biggr \}}^{2/5}\times \cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(x^{1/2})^{2}}{2\,\theta _{4}(x^{5/2})^{2}}}{\biggr ]}{\biggr \}}^{1/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/653ddfd03c750f090257220e797ef12f57d5a12e)


![{\displaystyle R{\big (}e^{-\pi }{\big )}={\frac {1}{2}}\varphi \,({\sqrt {5}}-\varphi ^{3/2})({\sqrt[{4}]{5}}+\varphi ^{3/2})=0.511428\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d2239d945b4400f5264c067197b803342551d9d)
![{\displaystyle q(k)=\exp {\big [}-\pi K({\sqrt {1-k^{2}}})/K(k){\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43ce6a2e5f468a1bce63fdd37a00bfecd4b335a3)
![{\displaystyle R{\big (}q(k){\big )}=\tan {\biggl \{}{\frac {1}{2}}\arctan y{\biggr \}}^{1/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} y{\biggr \}}^{2/5}=\left\{{\frac {{\sqrt {y^{2}+1}}-1}{y}}\right\}^{1/5}\left\{y\left[{\sqrt {{\frac {1}{y^{2}}}+1}}-1\right]\right\}^{2/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fc64c3e2822d40b917901360429284d24cbe293)
![{\displaystyle y={\frac {2k^{2}\,{\text{sn}}[{\tfrac {2}{5}}K(k);k]^{2}\,{\text{sn}}[{\tfrac {4}{5}}K(k);k]^{2}}{5-k^{2}\,{\text{sn}}[{\tfrac {2}{5}}K(k);k]^{2}\,{\text{sn}}[{\tfrac {4}{5}}K(k);k]^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7719b360c0d190bf112e626de3f87cc19e20e34e)

![{\displaystyle x=\left[{\frac {{\sqrt {5}}\,\eta (5\tau )}{\eta (\tau )}}\right]^{6}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2314c008974113c9585ab1e63248c776b59c0b02)

![{\displaystyle {\begin{aligned}&j(\tau )=-{\frac {(r^{20}-228r^{15}+494r^{10}+228r^{5}+1)^{3}}{r^{5}(r^{10}+11r^{5}-1)^{5}}}\\[6pt]&j(\tau )-1728=-{\frac {(r^{30}+522r^{25}-10005r^{20}-10005r^{10}-522r^{5}+1)^{2}}{r^{5}(r^{10}+11r^{5}-1)^{5}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/883827756d7f47131c78695dfb009752642db072)

![{\displaystyle {\begin{aligned}&j(5\tau )=-{\frac {(r^{20}+12r^{15}+14r^{10}-12r^{5}+1)^{3}}{r^{25}(r^{10}+11r^{5}-1)}}\\[6pt]&j(5\tau )-1728=-{\frac {(r^{30}+18r^{25}+75r^{20}+75r^{10}-18r^{5}+1)^{2}}{r^{25}(r^{10}+11r^{5}-1)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0654694c4cb81f6e887c2fe76573c7378e1202e)


![{\displaystyle {\begin{aligned}&z_{\infty }=-\left[{\frac {{\sqrt {5}}\,\eta (25\tau )}{\eta (5\tau )}}\right]^{6}-11,\ z_{0}=-\left[{\frac {\eta (\tau )}{\eta (5\tau )}}\right]^{6}-11,\ z_{1}=\left[{\frac {\eta ({\frac {5\tau +2}{5}})}{\eta (5\tau )}}\right]^{6}-11,\\[6pt]&z_{2}=-\left[{\frac {\eta ({\frac {5\tau +4}{5}})}{\eta (5\tau )}}\right]^{6}-11,\ z_{3}=\left[{\frac {\eta ({\frac {5\tau +6}{5}})}{\eta (5\tau )}}\right]^{6}-11,\ z_{4}=-\left[{\frac {\eta ({\frac {5\tau +8}{5}})}{\eta (5\tau )}}\right]^{6}-11\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfc22fc990829510a6e4dc7225adb6abe4ad177f)

























![{\displaystyle {\bigl [}R(e^{-2a})+\varphi {\bigl ]}{\bigl [}R(e^{-2b})+\varphi {\bigr ]}={\sqrt {5}}\,\varphi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41cf03a262ca7ba345d4adb584a74b89e1f72f56)

![{\displaystyle {\bigl [}R^{5}(e^{-2a})+\varphi ^{5}{\bigl ]}{\bigl [}R^{5}(e^{-2b})+\varphi ^{5}{\bigr ]}=5{\sqrt {5}}\,\varphi ^{5}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e791a2350a718cff4bbb54d7bd2ae8f5c2fbf6d2)







![{\displaystyle q(k)=\exp {\big [}-\pi K({\sqrt {1-k^{2}}})/K(k){\big ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e103968699b46b8638435465792de472cc5a077f)
![{\displaystyle k=\tan[{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\operatorname {arccsc}(a^{2})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7daf53c185d5126a6f836573079e44c54b13d02)
![{\displaystyle {\begin{aligned}x&={\frac {2-{\bigl \{}1-R[q(k)]{\bigr \}}{\bigl \{}1+R[q(k)^{2}]{\bigr \}}}{{\sqrt {R[q(k)]\,R[q(k)^{2}]}}\,{\sqrt[{4}]{4\cot \langle 4\arctan\{S\}\rangle -3}}}}\\&={\frac {2-{\bigl \{}1-R[q(k)]{\bigr \}}{\bigl \{}1+R[q(k)^{2}]{\bigr \}}}{{\sqrt {R[q(k)]R[q(k)^{2}]}}\,{\sqrt[{4}]{{\frac {2}{S-1}}+{\frac {2}{S+1}}+{\frac {1}{S}}-S-3}}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/685c5763932156ecc824ae9d8be60ab687407a17)
![{\displaystyle S=R[q(k)]\,R^{2}[q(k)^{2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2fcdd7b37eadcd19870e06b76bc198c952a77c8)

![{\displaystyle R^{5}[q(k)]=S\left({\frac {1-S}{1+S}}\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85926c9b781d096afba0c57300edd0daaf2420a8)

![{\displaystyle ({\sqrt[{4}]{5}}x)^{5}-5({\sqrt[{4}]{5}}x)-4({\tfrac {5}{4}}{\sqrt[{4}]{5}})=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61cbe3f71016c548429ccaa965215a70dd5684a1)
![{\displaystyle a={\tfrac {5}{4}}{\sqrt[{4}]{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58854d16aba0f4a3929b92e77c60e1cf4936b709)
![{\displaystyle k=\tan[{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\operatorname {arccsc}(a^{2})]={\tfrac {5^{5/4}+{\sqrt {25{\sqrt {5}}-16}}}{5^{5/4}+{\sqrt {25{\sqrt {5}}+16}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3325d9072bcc7241357faa1789ccb8f610d72ca)

![{\displaystyle R[q(k)]=0.5633613184\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f14c09d3a3e231c86765a5558de4dc567a5a9a45)
![{\displaystyle R[q(k)^{2}]=0.3706122329\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/953a83069f8350cffc6b99371d1aef0cfed50476)
![{\displaystyle x={\frac {2-{\bigl \{}1-R[q(k)]{\bigr \}}{\bigl \{}1+R[q(k)^{2}]{\bigr \}}}{{\sqrt {R[q(k)]\,R[q(k)^{2}]}}\,{\sqrt[{4}]{20\cot \langle 4\arctan\{R[q(k)]\,R[q(k)^{2}]^{2}\}\rangle -15}}}}=1.167303978\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d376cd22fe9212abeb1d720c8a4d16f5e3b8eed)
![{\displaystyle x^{5}-5x-4{\Bigl (}{\sqrt[{4}]{\tfrac {81}{32}}}{\Bigr )}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26c633789bedcf0852350bfe130dea2e4b7a1962)
![{\displaystyle a={\sqrt[{4}]{\tfrac {81}{32}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b08932766845ca177ab4d228ec02299e00664df)
![{\displaystyle r_{1}=R{\big (}e^{-\pi }{\big )}={\tfrac {1}{2}}\varphi \,({\sqrt {5}}-\varphi ^{3/2})({\sqrt[{4}]{5}}+\varphi ^{3/2})=0.511428\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf43bdad2722185a9a278aa7a3d39ee5c4b9fbe0)
![{\displaystyle r_{2}=R{\big (}e^{-2\pi }{\big )}={\sqrt[{4}]{5}}\,\varphi ^{1/2}-\varphi =0.284079\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a831e73343c7f98f716bab3de2dc8c20953883b)
![{\displaystyle r_{4}=R{\big (}e^{-4\pi }{\big )}={\tfrac {1}{2}}\varphi \,({\sqrt {5}}-\varphi ^{3/2})(-{\sqrt[{4}]{5}}+\varphi ^{3/2})=0.081002\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d9de6c6425583a93eca75d05cd0f7fa97b907aa)
![{\displaystyle {\begin{aligned}x&={\sqrt[{4}]{5}}\,{\frac {2-{\bigl \{}1-r_{1}{\bigr \}}{\bigl \{}1+r_{2}{\bigr \}}}{{\sqrt {r_{1}\,r_{2}}}\,{\sqrt[{4}]{20\cot \langle 4\arctan\{r_{1}\,r_{2}^{2}\}\rangle -15}}}}\\[6pt]&={\sqrt[{4}]{5}}\,{\frac {2-{\bigl \{}1-r_{2}{\bigr \}}{\bigl \{}1+r_{4}{\bigr \}}}{{\sqrt {r_{2}\,r_{4}}}\,{\sqrt[{4}]{20\cot \langle 4\arctan\{r_{2}\,r_{4}^{2}\}\rangle -15}}}}\\[6pt]&={\sqrt[{4}]{8}}=1.681792\dots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4f782ba7e718ea81519365e1e4bc278eb6a7c9f)