Principle of indifference
|
Read other articles:

SMA Negeri 1 PurwakartaLogo SMA Negeri 1 PurwakartaInformasiDidirikan1957JenisNegeriAkreditasiA[1]Nomor Statistik Sekolah301022001001Nomor Pokok Sekolah Nasional20217357Kepala SekolahDra. Hj Titin Kuraesin, M.Pd.KomiteDrs. Alit SukandiProgram jurusanIPA dan IPSRentang kelasX IPA, X IPS, XI IPA, XI IPS, XII IPA, XII IPSKurikulumKurikulum 2013 dan Kurikulum MerdekaStatusSMA RujukanAlamatLokasiJalan Kol. K. Singawinata No. 113, Kabupaten Purwakarta, Provinsi Jawa Barat, Indone...

Kenapa Harus Inul?Genre Drama Roman Musikal SutradaraArswendo AtmowilotoPemeran Inul Daratista Irgi Ahmad Fahrezi Torro Margens Chintami Atmanegara Anwar Fuady Renita Sukardi Ivanka Suwandi Negara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim2Jmlh. episode76ProduksiProduser eksekutifElly Yanti NoorProduserLeo SutantoDurasi60—90 menitRumah produksiLenza FilmDistributorSurya Citra MediaRilis asliJaringanSCTVRilisSabtu, 28 Juni 2003 –Sabtu, 3 Desember 2004 Kenapa Harus Inul? adal...

I Gusti Gde Raka I Gusti Gde Raka adalah seorang politikus Indonesia. Pada masa pendudukan Hindia Belanda oleh Jepang, ia bekerja pada bagian Kemakmuran dan kemudian pada Perbendaharaan. Pada bulan September 1945, ia diangkat sebagai Kepala Perbendaharaan Provinsi Sunda Kecil Pemerintah Republik Indonesia. Dari Maret 1946 sampai Juli 1949, ia ditawan oleh tentara Belanda. Pada bulan Juli 1949, ia dilepaskan, berangkat ke Jogjakarta dan bekerja sebagai ahli Kepala Keuangan pada Kementerian Keu...

Association football position England captain Leah Williamson (left) defends for Arsenal.In the sport of association football, a defender is an outfield player whose primary role is to stop attacks during the game and prevent the opposition from scoring. Defenders fall into five main categories: centre-backs, full-backs, defensive midfielders, sweepers, and wing-backs. The centre-back and full-back positions are most common in modern formations. The sweeper and wing-back roles are more specia...

العلاقات السيراليونية المصرية سيراليون مصر سيراليون مصر تعديل مصدري - تعديل العلاقات السيراليونية المصرية هي العلاقات الثنائية التي تجمع بين سيراليون ومصر.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة �...

Astronomical chronology, or astronomical dating, is a technical method of dating events or artifacts that are associated with astronomical phenomena. Written records of historical events that include descriptions of astronomical phenomena have done much to clarify the chronology of the Ancient Near East; works of art which depict the configuration of the stars and planets and buildings which are oriented to the rising and setting of celestial bodies at a particular time have all been dated th...

Carlos Santana Carlos Augusto Alves Santana (lahir 20 Juli 1947) merupakan seorang gitaris berkebangsaan Meksiko dan Amerika Serikat yang memenangkan nominasi Grammy Award. Dia merupakan anggota dari grup musik Santana. Dilahirkan di Autlán de Navarro. Dia berkarier di dunia musik sejak tahun 1966. Diskografi Album studio Love Devotion Surrender (1973) Illuminations (1974) Oneness — Silver Dreams Golden Reality (1979) The Swing of Delight (1980) Havana Moon (1983) Blues for Salvador (1987)...

مرداويج الزياري معلومات شخصية الميلاد العقد 890 فومن الوفاة سنة 935 أصفهان مكان الدفن قلعة غبري مواطنة إيران عائلة زياريون مناصب أمير آل زيار في المنصب319 – 323 وشمكير الحياة العملية المهنة عاهل تعديل مصدري - تعديل مَرْدَاوِي...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

Philip La FollettePhilip La Follette setelah ayahnya wafat pada 1925. Gubernur Wisconsin 27 dan 29Masa jabatan7 Januari 1935 – 2 Januari 1939WakilThomas J. O'MalleyLowongHenry A. GundersonLowongHerman L. EkernPendahuluAlbert G. SchmedemanPenggantiJulius P. HeilMasa jabatan5 Januari 1931 – 2 Januari 1933WakilHenry A. HuberPendahuluWalter J. Kohler, Sr.PenggantiAlbert G. Schmedeman Informasi pribadiLahirPhilip Fox La Follette(1897-05-08)8 Mei 1897Madison, Wisconsin, AS...

American record label Not to be confused with The Verve or The Verve Pipe. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Verve Records – news · newspapers · books · scholar · JSTOR (December 2017) (Learn how and when to remove this message) Verve RecordsParent companyVerve Label Group(Universal Music Group...

Maarn adalah sebuah bekas gemeente Belanda yang terletak di provinsi Utrecht. Pada tahun 2005 daerah ini memiliki penduduk sebesar 4260 jiwa. Artikel bertopik geografi atau tempat Belanda ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

Haitian empress Marie-Claire Heureuse Félicité Bonheur DessalinesEmpress consort of HaitiTenure2 September 1804 – 17 October 1806Coronation8 October 1804BornMay 8, 1758Léogâne, Saint-DomingueDied8 August 1858 (aged 99–100)Gonaïves, HaitiSpousePierre Lunic, deceased in 1795Jean-Jacques DessalinesFatherGuillaume BonheurMotherMarie-Sainte LobelotReligionRoman Catholic Empress Marie-Claire Heureuse Félicité Bonheur, Empress of Haiti (8 May 1758 – 8 August 1858[1]) was th...

Canadian actor Lang as Hamlet Matheson Alexander Lang (May 15, 1879 – April 11, 1948) was a Canadian-born stage and film actor and playwright. He is best remembered for his theatrical performances in Great Britain in Shakespeare plays. Biography Lang was born in Montreal, Quebec, Canada, the son of Rev. Gavin Lang of Inverness, Scotland, and a cousin of Cosmo Gordon Lang, who would later become Archbishop of Canterbury.[1] Lang was educated at Inverness College and the University of...

This article is about a defunct party. For the currently active party under Baburam Bhattarai, see Nepal Socialist Party. Political party in Nepal Naya Shakti Party, Nepal नयाँ शक्ति पार्टी, नेपालLeaderBaburam BhattaraiFounded12 June 2016 (7 years ago) (2016-06-12)Dissolved6 May 2019Split fromUnified Communist Party of Nepal (Maoist)Succeeded bySamajbadi Party, NepalHeadquartersBabarmahal, KathmanduStudent wingNaya Shakti Stu...

See also: Women's sport in Iraq Football leagueIraqi Women's Football LeagueFounded2016Country IraqConfederationAFCNumber of teams7 (since 2023–24)International cup(s)WAFF Women's Clubs ChampionshipCurrent championsAl-Quwa Al-Jawiya (1st title) (2023–24)Most championshipsGhaz Al-ShamalNaft Al-ShamalAl-Quwa Al-Jawiya(1 title each)Current: 2023–24 Iraqi Women's Football League The Iraqi Women's Football League (Arabic: الدوري العراقي للسيدات) is the league com...
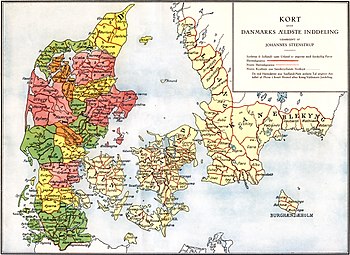
Country subdivision in Scandinavia A syssel is a historical type of country subdivision in Denmark and elsewhere in Scandinavia. The mediaeval Danish sysler may be compared to the fylker of Norway, the landskaps of Sweden and Finland, the shires of England and Scotland, and the Gaue of the Holy Roman Empire. A syssel was subdivided into a number of hundreds or herreder. The name still can be found in the Danish district of Vendsyssel, as well as in a governmental title, sýslumenn, in Iceland...

This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (March 2024) The Gregory Hall on the campus of University of Illinois at Urbana–Champaign hosted an important meeting of the National Association of Educational Broadcasters in the 1940s, that spawned both PBS and NPR.[citation needed]In the United States, other than a few direct services, p...

2023 play by Jack Thorne The Motive and the CueWest End Promotional PosterWritten byJack ThorneDirected bySam MendesDate premiered21 April 2023Place premieredNational TheatreLondonOriginal languageEnglishSubjectHistory, Acting, ShakespeareGenreDramaSetting1960s New York City The Motive and the Cue is a play written by Jack Thorne. The production, directed by Sam Mendes, premiered on 21 April 2023 at the National Theatre in London. The play revolves around the history behind the 1964 Broadway ...

American college football season 2020 Nevada Wolf Pack footballFamous Idaho Potato Bowl championFamous Idaho Potato Bowl, W 38–27 vs. TulaneConferenceMountain West ConferenceRecord7–2 (6–2 MW)Head coachJay Norvell (4th season)Offensive coordinatorMatt Mumme (4th season)Offensive schemeAir raidDefensive coordinatorBrian Ward (1st season)Base defenseMultipleCaptains Carson Strong Jermaine Ledbetter Lawson Hall Sam Hammond Seasons← 20192021 → ...






