Nowhere-zero flow
|
Read other articles:

For other uses, see Arsenal (disambiguation). Football clubArsenal FCFull nameArsenal Football ClubFounded1983[1]GroundSetsoto StadiumMaseru, LesothoCapacity20,000 Arsenal Football Club is a Mosotho football club based in Maseru.[2] Achievements Lesotho Premier League: 3 1989, 1991, 1993 Lesotho Cup: 3 1989, 1991, 1998 Performance in CAF competitions African Cup of Champions Clubs: 3 appearances 1990: Second Round 1992: First Round 1994: First Round CAF Cup: 1 appearances 1995...

Keramik Dehua, salah satu jenis kerajinan keramik paling dikenal di Tiongkok Dehua (德化縣/Minnan: Tek-hòe-koān/Tek-hòe-kūiⁿ) adalah sebuah kabupaten yang terletak di dalam Kota Quanzhou, Fujian.[1] Kabupaten Dehua dikenal sebagai pusat produksi keramik di Tiongkok. Pada zaman dahulu ia dianggap sebagai salah satu dari tiga ibu kota keramik bersama Jingdezhen (Jiangxi) dan Liling (Hunan).[1] Produksi keramik Dehua telah dimulai sejak periode Tang dan mencapai zaman ke...

Spanish cyclist For other people named Pedro Delgado, see Pedro Delgado (disambiguation). In this Spanish name, the first or paternal surname is Delgado and the second or maternal family name is Robledo. Pedro DelgadoDelgado in 2016Personal informationFull namePedro Delgado RobledoNicknamePericoBorn (1960-04-15) 15 April 1960 (age 63)Segovia, Castile and León, SpainHeight1.71 m (5 ft 7+1⁄2 in)Weight64 kg (141 lb; 10 st 1 lb)Team info...

Untuk kegunaan lain, lihat PBB (disambiguasi). Partai Bulan Bintang Ketua umumYusril Ihza MahendraSekretaris JenderalAfriansyah NoorDibentuk17 Juli 1998; 25 tahun lalu (1998-07-17)Kantor pusatPasar Minggu, Jakarta Selatan, DKI JakartaIdeologiDemokrasi Islam[1]Nasionalisme religius[2]Konservatisme[3]PancasilaPosisi politikSayap-kananAgamaIslamKursi di DPR0 / 575 Kursi di DPRD I7 / 2.232 Kursi di DPRD II214 / 17.340 Situs webwww.partaibulanbintang.or.idPolitik ...

Dighton was known for his illistraded portrait of the first, so called English dandy. Sir Henry Frederick Cooke (1819)by Richard Dighton Richard Dighton (1795 in London – 13 April 1880 in London), was an English artist in the Regency period, best known for his many satirical profile portraits of contemporary London celebrities and characters. He was the son and apprentice of another noted caricaturist, Robert Dighton (1752–1814), and brother of the battle-scene painter Denis Dighton and o...

Tetua Adat di Gorontalo Gara'i (dibaca: gara i) merupakan sebuah Upacara Penobatan atau Pemberian Gelar Adat kepada orang yang telah wafat atau meninggal atas darma bakti serta kontribusinya bagi daerah, bangsa, dan agama.[1] Gelar Gara'i ditetapkan dari hasil permufakatan para pemangku adat (Bate) dari 5 negeri (Pohala'a) di Gorontalo (Ulimo lo Pohalaa) yakni Pohala'a Suwawa, Pohala'a Limboto, Pohala'a Gorontalo, Pohala'a Atinggola, dan Pohala'a Bulango.[2] Proses Penentuan G...

Filomela dan Prokne Filomela (bahasa Yunani Kuno: Φιλομήλα, translit. Philoméla) adalah tokoh kecil dalam mitologi Yunani yang sering disebut sebagai simbol langsung dan kiasan dalam karya sastra dan seni dalam kanon barat. Dia diidentifikasikan sebagai putri Athena sebagai putri yang lebih muda dari kedua putri Pandion I, Raja Athena kedelapan dan Zeuxippe.[1] Saudara perempuannya Prokne adalah istri Raja Tereus dari Trakia. Referensi ^ Pseudo-Apollodoro, Biblioteca...

Pictures encoded as binary data For broader coverage of this topic, see Digital imaging. A digital image is an image composed of picture elements, also known as pixels, each with finite, discrete quantities of numeric representation for its intensity or gray level that is an output from its two-dimensional functions fed as input by its spatial coordinates denoted with x, y on the x-axis and y-axis, respectively.[1] Depending on whether the image resolution is fixed, it may be of vecto...

Agriculture using powered machinery A cotton picker at work. The first successful models were introduced in the mid-1940s and each could do the work of 50 hand pickers. Mechanised agriculture or agricultural mechanization is the use of machinery and equipment, ranging from simple and basic hand tools to more sophisticated, motorized equipment and machinery, to perform agricultural operations.[1] In modern times, powered machinery has replaced many farm task formerly carried out by man...

Pour les articles homonymes, voir Bloomfield. Mike BloomfieldMike Bloomfield, photographié par Elliott Landy en 1960.BiographieNaissance 28 juillet 1943ChicagoDécès 15 février 1981 (à 37 ans)San FranciscoSépulture Hillside Memorial ParkNationalité américaineFormation New Trier High School (en)Cornwall Academy (d)Activités Musicien, pianiste, guitariste, chanteurPériode d'activité 1964-1981Autres informationsInstruments Guitare, pianoLabel Columbia RecordsGenre artistique Blue...

Mapei Stadium - Città del TricoloreStadio Città del Tricolore (2012-2014)Stadio Giglio (1994-2012) Vista esterna dello stadio Informazioni generaliStato Italia UbicazionePiazzale Atleti Azzurri d'Italia 1, I-42124 Reggio Emilia Inizio lavori1994 Inaugurazione1995 Costo25000000000 L Ristrutturazione2004, 2010, 2014-2015 ProprietarioMirabello 2000 S.p.A.[1] (1995-2006)Tribunale fallimentare di Reggio Emilia (2006-2013)Mapei S.p.A.[2] (2013-) ProgettoAldo PavoniCarlo Minem...

طواف أندلوسيا 2018 تفاصيل السباقسلسلة64. طواف أندلوسيامنافسةطواف أوروبا للدراجات 2018 2.HCمراحل5التواريخ14 – 18 فبراير 2018المسافات708٫1 كمالبلد إسبانيانقطة البدايةميخاسنقطة النهايةبرباطالفرق22عدد المتسابقين في البداية154عدد المتسابقين في النهاية135متوسط السرعة40٫011 كم/سالمنصة�...
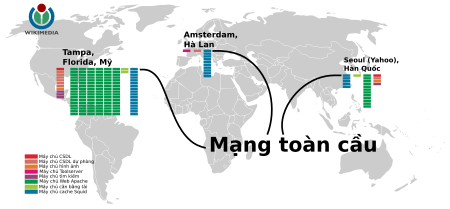
Bài viết này cần được cập nhật do có chứa các thông tin có thể đã lỗi thời hay không còn chính xác nữa. Bạn có thể giúp Wikipedia bằng cách cập nhật cho bài viết này. Meta-Wiki đổi hướng tới đây. Đối với trang dự án về Meta Wikimedia, xem Wikipedia:Meta. Wikimedia chuyển hướng đến đây. Đừng nhầm lẫn với MediaWiki. Wikimedia FoundationBiểu trưng của Wikimedia FoundationThành lậpSt. Petersburg, Fl...

Short story collection by Agatha Christie The Under Dog and Other Stories Dust-jacket illustration of the first US editionAuthorAgatha ChristieCountryUnited KingdomLanguageEnglishSeriesHercule PoirotGenreDetective fictionshort storyPublisherDodd Mead and CompanyPublication date1951Media typePrint (hardback & paperback)Pages248Preceded byTaken at the Flood Followed byMrs McGinty's Dead The Under Dog and Other Stories is a short story collection written by Agatha C...

Not to be confused with Royston, Glasgow. Human settlement in ScotlandRobroystonScottish Gaelic: Baile Raibeart Ruadh2018 aerial view showing Robroyston (top), Balornock (bottom left) and Barmulloch (bottom right) as well as the M80; 'Old Robroyston' is to the far centre-right of the imageRobroystonLocation within GlasgowOS grid referenceNS637690Council areaGlasgow City CouncilLieutenancy areaGlasgowCountryScotlandSovereign stateUnited KingdomPost townGLASGOWPostcode&...

British historian, academic, and author (born 1947) This article is about the British historian. For the British-Canadian poet, see Robert W. Service. Robert ServiceFBAService speaking at the Tallinn Literature Festival HeadRead in May 2011BornRobert John Service (1947-10-29) 29 October 1947 (age 76)United KingdomAwardsDuff Cooper Prize (2009)Academic backgroundAlma materKing's College, CambridgeAcademic workInstitutionsUniversity of OxfordMain interestsRussian history (1894–)Notable w...

Mississippi River Band of Chippewa Indians (Ojibwe: Gichi-ziibiwininiwag) or simply the Mississippi Chippewa, are a historical Ojibwa Band inhabiting the headwaters of the Mississippi River and its tributaries in present-day Minnesota. According to the oral history of the Mississippi Chippewa, they were primarily of the southern branch of Ojibwe who spread from the Fifth Stopping Place of Baawiting (Sault Ste. Marie region) along Lake Superior's southern shores until arriving at the Sixth Sto...

香港仔Lion Rock Daily類型日報(周一至周五發行,法定假期除外)版式小報持有者大公文匯傳媒集團出版商三友印務有限公司(承印)創刊日2018年4月9日 (2018-04-09)(正式出版,6年98天)政治立場親建制派語言繁體中文总部 香港香港仔田灣海傍道7號興偉中心2至3樓售價免費報紙網站lionrockdaily.com 《香港仔》(英語:Lion Rock Daily)是香港大公文匯傳媒集團旗下的免費報章�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nakafurano, Hokkaido – news · newspapers · books · scholar · JSTOR (October 2022) (Learn how and when to remove this message) You can help expand this article with text translated from the corresponding article in Japanese. (June 2022) Click [show] for imp...

Marvel comics character Comics character Bob, Agent of HydraPublication informationPublisherMarvel ComicsFirst appearanceCable & Deadpool #38(May 2007)Created byFabian Nicieza (writer)Reilly Brown (artist)In-story informationAlter egoRobert DobalinaSpeciesHumanTeam affiliations X Agency Hydra PartnershipsDeadpool Bob, Agent of Hydra (Robert Dobalina), is a fictional character appearing in American comic books published by Marvel Comics. The character is depicted as an antihero and a sidek...




















