Millman's theorem

In electrical engineering, Millman's theorem^[1] (or the parallel generator theorem) is a method to simplify the solution of a circuit. Specifically, Millman's theorem is used to compute the voltage at the ends of a circuit made up of only branches in parallel.

It is named after Jacob Millman, who proved the theorem.

Explanation

Let $e_{k}$ be the generators' voltages. Let $R_{k}$ be the resistances on the branches with voltage generators $e_{k}$ . Then Millman states that the voltage at the ends of the circuit is given by:^[2]

v={\frac {\sum {\frac {e_{k}}{R_{k}}}}{\sum {\frac {1}{R_{k}}}}}.

That is, the sum of the short circuit currents in branch divided by the sum of the conductances in each branch.

It can be proved by considering the circuit as a single supernode.^[3] Then, according to Ohm and Kirchhoff, the voltage between the ends of the circuit is equal to the total current entering the supernode divided by the total equivalent conductance of the supernode. The total current is the sum of the currents in each branch. The total equivalent conductance of the supernode is the sum of the conductance of each branch, since all the branches are in parallel.^[4]

Branch variations

Current sources

One method of deriving Millman's theorem starts by converting all the branches to current sources (which can be done using Norton's theorem). A branch that is already a current source is simply not converted. In the expression above, this is equivalent to replacing the $e_{k}/R_{k}$ term in the numerator of the expression above with the current of the current generator, where the kth branch is the branch with the current generator. The parallel conductance of the current source is added to the denominator as for the series conductance of the voltage sources. An ideal current source has zero conductance (infinite resistance) and so adds nothing to the denominator.^[5]

Ideal voltage sources

If one of the branches is an ideal voltage source, Millman's theorem cannot be used, but in this case the solution is trivial, the voltage at the output is forced to the voltage of the ideal voltage source. The theorem does not work with ideal voltage sources because such sources have zero resistance (infinite conductance) so the summation of both the numerator and denominator are infinite and the result is indeterminate.^[6]

References

^ Millman, Jacob (1940). "A Useful Network Theorem". Proceedings of the IRE. 28 (9): 413–417. doi:10.1109/JRPROC.1940.225885.
^ Bakshi & Bakshi, p. 7-28
^ Bakshi & Bakshi, p. 3-7
^ Ghosh & Chakraborty, p. 172
^ Wadhwa, p. 88
^ Singh, p. 64

Bakshi, U.A.; Bakshi, A.V., Network Analysis, Technical Publications, 2009 ISBN 818431731X.
Ghosh, S.P.; Chakraborty, A.K., Network Analysis and Synthesis, Tata McGraw-Hill, 2010 ISBN 0070144788.
Singh, S.N., Basic Electrical Engineering, PHI Learning, 2010 ISBN 8120341880.
Wadhwa, C.L., Network Analysis and Synthesis, New Age International ISBN 8122417531'

Read other articles:

Estonia

Untuk kegunaan lain, lihat Estonia (disambiguasi). Republik EstoniaEesti Vabariik (Estonia) Bendera Lambang Semboyan: —Lagu kebangsaan: Mu isamaa, mu õnn ja rõõm (Indonesia: Tanah airku, kebahagiaanku) Perlihatkan BumiPerlihatkan peta EropaPerlihatkan peta BenderaLokasi Estonia (hijau gelap)– di Eropa (hijau & abu-abu)– di Uni Eropa (hijau)Ibu kota(dan kota terbesar)Tallinn59°25′N 24°45′E / 59....

Ĥ

Latin letter H with circumflex; used in Esperanto This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ĥ – news · newspapers · books · scholar · JSTOR (September 2014) (Learn how and when to remove this template message) Part of a series onEsperanto flag Esperanto Language Grammar Phonology Orthography (Braille)...

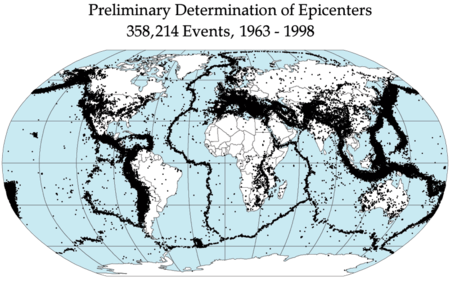
Seismic zone

Area of seismicity potentially sharing a common cause Earthquake epicenters 1963–98 In seismology, a seismic zone or seismic belt is an area of seismicity potentially sharing a common cause. It may also be a region on a map for which a common areal rate of seismicity is assumed for the purpose of calculating probabilistic ground motions. An obsolete definition is a region on a map in which a common level of seismic design is required.[1] A type of seismic zone is a Wadati–Benioff ...

Randy Skretvedt

American journalist This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is ...

趙家驤

追晉陸軍二級上將趙家驤將軍个人资料出生1910年大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)（47—48歲） † 中華民國福建省金門縣国籍中華民國政党中國國民黨获奖青天白日勳章（追贈）军事背景效忠中華民國服役國民革命軍中華民國陸軍服役时间1924年－1958年军衔二級上將（追晉）部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Downham Market

Market town in Norfolk, England Market town in EnglandDownham MarketMarket townClock Tower in Downham MarketDownham MarketLocation within NorfolkArea5.20 km2 (2.01 sq mi)Population9,994 (2011 Census)[1]• Density1,922/km2 (4,980/sq mi)OS grid referenceTF611032DistrictKing's Lynn and West NorfolkShire countyNorfolkRegionEastCountryEnglandSovereign stateUnited KingdomPost townDOWNHAM MARKETPostcode districtPE38Dialling code013...

Maureen Connolly Memorial Dallas 1973

Maureen Connolly Memorial Dallas 1973 Sport Tennis Data 5 marzo - 11 marzo Edizione 2a Superficie Sintetico indoor Campioni Singolare Virginia Wade Doppio Evonne Goolagong / Janet Young Il Maureen Connolly Memorial Dallas 1973 è stato un torneo di tennis giocato sul sintetico indoor. È stata la 2ª edizione del torneo, che fa parte del Women's International Grand Prix 1973. Si è giocato a Dallas negli USA dal 5 all'11 marzo 1973. Indice 1 Campionesse 1.1 Singolare 1.2 Doppio 2 Collegament...

周處除三害 (電影)

周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)（台灣） 2023年11月2日 (2023-11-02)（香�...

Gugusdepan Gerakan Pramuka

Gugusdepan, disingkat Gudep adalah suatu kesatuan organik dalam Gerakan Pramuka yang merupakan wadah untuk menghimpun anggota Gerakan Pramuka sebagai peserta didik dan pembina Pramuka, serta berfungsi sebagai pangkalan keanggotaan peserta didik.[1] Ketentuan umum Anggota Gerakan Pramuka yang berkedudukan sebagai peserta didik, pembina Pramuka dan anggota Majlis Pembimbing Gugusdepan (Mabigus) dihimpun dalam Gudep. Gudep dapat dibentuk di: Lembaga pendidikan umum seperti sekolah dan Pe...

القوات المسلحة الأمريكية

القوات المسلحة الأمريكية الدولة الولايات المتحدة التأسيس 14 يونيو 1775؛ منذ 248 سنة (1775-06-14)[ا] شعار مكتوب هذا هو ما سندافع عنه الاسم الأصلي القوات المسلحة للولايات المتحدة الأمريكية ألقاب الجيش الأمريكي اسم آخر القوات الأمريكية الفروع القوات البرية للولايات...

Maja Wallstein

German politician Maja WallsteinMember of the BundestagIncumbentAssumed office 2021 Personal detailsBorn (1986-03-18) 18 March 1986 (age 38)Cottbus, East Germany(now Germany)Political partySPDAlma materUniversity of PotsdamJagiellonian University Maja Scarlett Wallstein (born 18 March 1986) is a German politician of the Social Democratic Party (SPD) who has been serving as a member of the Bundestag since 2021. Early life and career Wallstein was born 1986 in the East German city of C...

Samnites

Italic people living in Samnium in south-central Italy Samnite soldiers depicted on a tomb frieze in Nola. From the 4th Century BC The Samnites (Oscan: Safineis) were an ancient Italic people who lived in Samnium, which is located in modern inland Abruzzo, Molise, and Campania in south-central Italy. Italy in 400 BC, with the Samnites living in the dark green region. An Oscan-speaking people, who originated as an offshoot of the Sabines, they formed a confederation consisting of four tribes: ...

Daniel Ricciardo

Daniel RicciardoDaniel Ricciardo nel 2022Nazionalità Australia Altezza180 cm Automobilismo CategoriaFormula 1 RuoloPilota Squadra RB CarrieraCarriera in Formula 1Esordio10 luglio 2011 Stagioni2011- Scuderie HRT 2011 Toro Rosso 2012-2013 Red Bull 2014-2018 Renault 2019-2020 McLaren 2021-2022 AlphaTauri 2023 RB 2024- Miglior risultato finale3º (2014, 2016) GP disputati249 (248 partenze) GP vinti8 Podi32 Punti ottenuti1 326 Pole position3 Giri ...

Trinity (British TV series)

British television drama series TrinityCreated byKieron QuirkeRobin FrenchDirected byColin TeagueDeclan O'DwyerStephen WoolfendenStarringCharles DanceClaire SkinnerAntonia BernathChristian CookeReggie YatesIsabella CalthorpeElen RhysArnab ChandaMark WoodPaul HunterMichael HiggsTom HughesDavid OakesRod ArthurAnthony CalfCountry of originUnited KingdomOriginal languageEnglishNo. of series1No. of episodes8 (list of episodes)ProductionProducerSue HowellsEditorXavier RussellRunning time60 minutes ...

Don Johnson Memorial Cup

The Don Johnson Memorial Cup, formerly Don Johnson Cup, is the Junior B ice hockey championship for Atlantic Canada, including Nova Scotia, Newfoundland, New Brunswick, and Prince Edward Island as of 2014. From 1982 until 1990 and 1997 until 2013, the Don Johnson Cup was emblematic of the Junior B championship of the Atlantic Provinces of Canada -- Nova Scotia, Newfoundland, New Brunswick, and Prince Edward Island. The cup is named in honour of Don Johnson, a sports enthusiast who dedicated ...

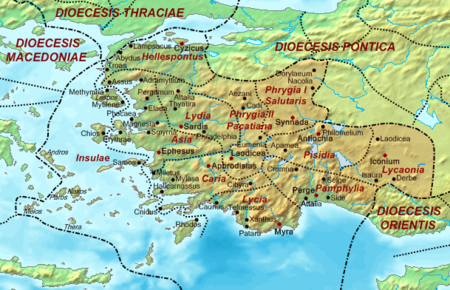
Satala in Lydia

Titular bishopric Asia minor 400AD Satala (Ancient Greek: Σάταλα) or Satala in Lydia was a Roman era city[1][2] and Bishopric[3] in ancient Lydia. Location Its site is located near Adala in Asiatic Turkey.[4][5] Pagan Religion The city worshiped the typical mother and son pantheon found throughout Anatolia, and although a temple was built it did not mint coint as the town was only a village. It was part of a decapolis called the Katakekaumene, and...

Wynn Palace

Luxury hotel and casino in Macau Wynn Palace永利皇宮 (Yue Chinese)Palácio Wynn (Portuguese) Location Cotai, Macau, Special administrative regions of ChinaOpening date22 August 2016; 7 years ago (22 August 2016)ThemeFloralNo. of rooms1,706Total gaming space39,000 square metres (420,000 sq ft)Signature attractions8-acre performance lake, SkyCab gondolas,[1] retail, dining, entertainment, convention venuesNotable restaurantsWing Lei Palace, SW Steakh...

PyPy

Alternative implementation of the Python programming language Not to be confused with PyPI, the Python official third-party software repository. Initial releasemid 2007; 17 years ago (2007)Stable release7.3.16[1] (23 April 2024; 3 months ago (23 April 2024)) Repositorygithub.com/pypy/pypy Written inRPythonOperating systemCross-platformTypePython interpreter and compiler toolchainLicenseMITWebsitepypy.org PyPy (/ˈpaɪpaɪ/) is an implementati...

Durham, North Carolina

City in North Carolina, United StatesDurhamCityDurham skylineDuke UniversityDuke Memorial UMCBennett PlaceCarolina TheatreDurham Performing Arts CenterAmerican Tobacco Historic District FlagSealLogoNickname(s): Bull City,[2] City of Medicine[3]Interactive map of DurhamDurhamShow map of North CarolinaDurhamShow map of the United StatesCoordinates: 35°58′43″N 78°54′00″W / 35.97861°N 78.90000°W / 35.97861; -78.90000CountryUnited StatesSta...

File sharing

Practice of distributing or providing access to digitally stored information Part of a series onFile sharing Technologies File hosting services Online video platform Peer to peer Usenet Web hosting WebRTC XDCC Video on demand sites 123Movies Dailymotion PeerTube Putlocker YouTube BitTorrent sites 1337x Demonoid ExtraTorrent EZTV isoHunt FitGirl Repacks KickassTorrents Nyaa Torrents RARBG Rutracker.org Tamil Rockers The Pirate Bay YIFY YourBittorrent Academic/scholarly ICanHazPDF Internet Arch...

PROFILPELAJAR.COM