Mathematics in Ancient Egypt: A Contextual History
|
Read other articles:

Jalan Raya Trans-PapuaPersimpangan besarUjung Barat:Sorong JayapuraUjung Timur:MeraukeSistem jalan bebas hambatanJalan Nasional Indonesia Sistem Jalan di Indonesia Jalan Tol Jalan raya Jalan Trans Papua adalah jaringan jalan nasional yang menghubungkan setiap provinsi di Papua, membentang dari Kota Sorong di Papua Barat Daya hingga Merauke di Papua Selatan, dengan total panjang mencapai 4.330,07 kilometer (km). Total panjang tersebut terbagi atas 3.259,45 km di Provinsi Papua -...

Esociformes Berbagai anggota famili esocidae Umbra krameri Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Superordo: Protacanthopterygii Ordo: EsociformesBleeker, 1859 Famili Esocidae G. Cuvier, 1817 Umbridae Bonaparte, 1845 Sinonim Esocoidei Bleeker, 1859 Haplomi Esocae Umbriformes Günther, 1866 Esociformes adalah ordo kecil ikan bersirip kipas yang hanya terdiri dari dua famili, yakni Umbridae dan Esocidae. Ordo ini berkerabat dekat dengan ordo Salmoniformes y...

Baptisterium LateranBattistero lateranenseInterior baptisterium41°53′10.14″N 12°30′15.44″E / 41.8861500°N 12.5042889°E / 41.8861500; 12.5042889Koordinat: 41°53′10.14″N 12°30′15.44″E / 41.8861500°N 12.5042889°E / 41.8861500; 12.5042889LokasiRomeNegara ItaliaArsitekturTipe arsitekturBaptisteriumPeletakan batu pertama440 Baptisterium Lateran (Italia: Battistero lateranensecode: it is deprecated ) adalah sebuah baptister...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Ulysses S. Grant Presiden Amerika Serikat ke-18Masa jabatan4 Maret 1869 – 4 Maret 1877Wakil PresidenSchuyler Colfax (1869-1873),Henry W...
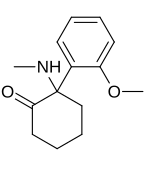
Not to be confused with Methoxetamine. Methoxyketamine Names IUPAC name 2-(2-Methoxyphenyl)-2-(methylamino)cyclohexanone Identifiers CAS Number 7063-51-6 Y6728-62-7 (HCl) Y 3D model (JSmol) Interactive image ChemSpider 27470964 PubChem CID 57483650 UNII U4I8JIS24N Y2OVB5UO35R (HCl) Y CompTox Dashboard (EPA) DTXSID30990849 InChI InChI=1S/C14H19NO2/c1-15-14(10-6-5-9-13(14)16)11-7-3-4-8-12(11)17-2/h3-4,7-8,15H,5-6,9-10H2,1-2H3Key: OYAUVHORXFUVAJ-UHFFFAOYSA-NInC...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (juillet 2018). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. Édouard de Cazenove de PradinesFonctionsDéputé ...

Town in Brandenburg, GermanyDrebkau DrjowkTownTown hall Coat of armsLocation of Drebkau within Spree-Neiße district Drebkau Show map of GermanyDrebkau Show map of BrandenburgCoordinates: 51°39′N 14°13′E / 51.650°N 14.217°E / 51.650; 14.217CountryGermanyStateBrandenburgDistrictSpree-Neiße Subdivisions10 OrtsteileGovernment • Mayor (2018–26) Paul Köhne[1] (CDU)Area • Total142.94 km2 (55.19 sq mi)Elevation87&...

Questa voce sull'argomento centri abitati del Paraná è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. União da Vitóriacomune União da Vitória – Veduta LocalizzazioneStato Brasile Stato federato Paraná MesoregioneSudeste Paranaense MicroregioneUnião da Vitória AmministrazioneSindacoPedro Ivo Ilkiv (PT) dal 2013 Data di istituzione1890 TerritorioCoordinate26°13′35″S 51°03′42″W / 26.226389°S 51.061...

Archaeocyatha Periode Tommotium - Kambrium Tengah PreЄ Є O S D C P T J K Pg N ↓ TaksonomiSuperkerajaanEukaryotaKerajaanAnimaliaFilumPoriferaKelasArchaeocyatha Tata namaSinonim takson Cyathospongia Okulitch, 1935 Pleospongia Okulitch, 1935 lbs Archaeocyatha (/ˈɑːrkioʊsaɪəθə/, 'mangkok kuno') adalah sebuah takson punah dari spons laut sesil pembangun karang[1] yang hidup di perairan hangat tropis dan subtropis pada periode Kambrium. Diyakini bahwa pusat kemunculan Archae...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Taipei Nan Shan Plaza – news · newspapers · books · scholar · JSTOR (December 2017) (Learn how and when to remove this message) Office building, department store in Taipei, TaiwanTaipei Nan Shan Plaza臺北南山廣場Taipei Nan Shan Plaza in 2023General inform...

Historic house in Massachusetts, United States United States historic placeFairbanks HouseU.S. National Register of Historic PlacesU.S. National Historic Landmark Fairbanks House in 2013Show map of MassachusettsShow map of the United StatesInteractive map showing the location of Fairbanks HouseLocation511 East Street, Dedham, MassachusettsCoordinates42°14′36″N 71°10′04″W / 42.24333°N 71.16778°W / 42.24333; -71.16778Builtca. 1637[1]NRHP referenc...

У этого топонима есть и другие значения, см. Ревда. ГородРевда вид на город с Лысой горы Флаг Герб 56°48′ с. ш. 59°55′ в. д.HGЯO Страна Россия Статус Город областного подчинения Субъект Федерации Свердловская область Городской округ Ревда Глава городского округа �...

Voce principale: Campionato mondiale di calcio 1974. Finale del campionato mondiale di calcio 1974I tedeschi occidentali Wolfgang Overath e Gerd Müller sollevano la coppa FIFAInformazioni generaliSport Calcio Competizione1974 FIFA World Cup knockout stage Data7 luglio 1974 CittàMonaco di Baviera ImpiantoStadio Olimpico Spettatori75 200 Dettagli dell'incontro Paesi Bassi Germania Ovest 1 2 Arbitro Jack Taylor (Inghilterra) Successione ← Finale del campionato mondiale di calc...

Mid-ocean ridge in the South Atlantic between the South American Plate and the Antarctic Plate Bathymetric map of the South American-Antarctic Ridge The South American–Antarctic Ridge or simply American-Antarctic Ridge (SAAR or AAR) (in Spanish: Dorsal Antártico-Americana) is the tectonic spreading center between the South American Plate and the Antarctic Plate. It runs along the sea-floor from the Bouvet Triple Junction in the South Atlantic Ocean south-westward to a major transform fault...

Докладніше: Збірна України з футболу Країни за кількістю матчів їхніх збірних проти збірної України. Список включає всіх суперників національної збірної України в офіційних матчах, починаючи з першого матчу проти збірної Угорщини 29 квітня 1992 року. Станом на 26 березня ...

Voce principale: Associazione Calcio Ancona. Ancona CalcioStagione 1996-1997Sport calcio Squadra Ancona Allenatore Giuseppe Petrelli poi Mario Colautti poi Fabio Brini Presidente Angelo Deodati (Amministratore Unico) Serie C12º posto nel girone B. Promossa in Serie B. Maggiori presenzeCampionato: Cesaretti, Tentoni (33) Miglior marcatoreCampionato: Lucidi, Tentoni (5) 1995-1996 1997-1998 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Ancona C...

Political party in Australia For the Australian party (1989–1991), Joh Bjelke-Petersen, see Australian Conservative Party. For the Australian party (1984–1998), see Conservative Party of Australia. Australian Conservatives LeaderCory Bernardi[a]FounderCory BernardiFounded7 February 2017; 7 years ago (7 February 2017)[b]Dissolved25 June 2019Split fromLiberal PartyHeadquartersKing William Street, Kent Town, South Australia 5067Membership (2017) 22,000[c...

Alben William BarkleyAlben Barkley Wakil Presiden Amerika SerikatMasa jabatan20 Januari 1949 – 20 Januari 1953PendahuluHarry S. TrumanPenggantiRichard Milhous Nixon Informasi pribadiLahir(1877-11-24)24 November 1877Lowes, Kentucky, Amerika SerikatMeninggal30 Mei 1956(1956-05-30) (umur 78)Lexington, Virginia, Amerika SerikatPartai politikDemokratSuami/istriJane Hadley BarkleyPekerjaanJaksaSunting kotak info • L • B Alben William Barkley lahir di dekat Lowes, Grave...

明朝关西八卫 赤斤蒙古卫,明朝关西八卫之一,简称赤斤卫,又作赤金卫。 明朝 明朝永乐二年(1404年)元朝丞相苦术之子塔力尼投降明朝,以其所部在赤斤站设置赤斤蒙古千户所,在今甘肃省玉门市西北赤金堡。永乐八年(1410年)升为赤斤卫,正德年间被吐鲁番汗国所破,当地人内徙肃州的南山,赤斤城空。 清朝 清圣祖康熙五十七年(1718年),恢复赤金卫,清世宗雍正...

British writer and illustrator Fred T. Jane with his Naval War Game in 1898 Heresies of Sea Power (1906) by Fred T. Jane published by Longmans, Green, and Co. John Fredrick Thomas Jane (6 August 1865 – 8 March 1916) was an author, war gamer, and founding editor of All the World's Fighting Ships and All the World's Airships. Biography Jane was born in Richmond, Surrey, England, but worked most of his life in Portsmouth. His father was a Church of England vicar. He attended Exeter School.[...
