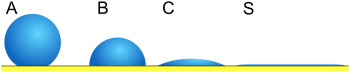
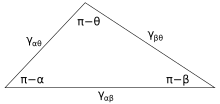
Ideal surface
|
Read other articles:

Itik penyerok Spatula clypeata jantan Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Anseriformes Subordo: Anseres Superfamili: Anatoidea Famili: Anatidae Subfamili: Anatinae Genus: SpatulaBoie, F, 1822 Spesies tipe Anas clypeataLinnaeus, 1758 Spesies Lihat teks Sinonim Anas (Pterocyanea) Bonaparte 1841[1] Querquedula Stephens 1824 Querquedula Oken 1817 nomen nudum Rhynchaspis Stephens 1824 Rhynchoplatus Berthold 1827 Cyanopterus Bonaparte18...

British broadcaster This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Glen Mic...

Former museum in New York City KGB Espionage MuseumLocation within ManhattanFormer nameKGB Spy MuseumEstablishedJanuary 17, 2019 (2019-01-17)Location245 West 14th St., New York, New York, United StatesCoordinates40°44′14″N 73°59′51″W / 40.737358°N 73.997451°W / 40.737358; -73.997451TypeHistory MuseumCollection sizeOver 3,900 ObjectsWebsitehttps://kgbespionagemuseum.org/ The KGB Espionage Museum was a museum dedicated to the unbiased presenta...

Languages of Europe and South Asia before the arrival of Indo-European languages Not to be confused with Proto-Indo-European language or Paleo-European languages. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citation...

Town in Saskatchewan, Canada Town in Saskatchewan, CanadaCuparTownCuparLocation of Cupar in SaskatchewanShow map of SaskatchewanCuparCupar (Canada)Show map of CanadaCoordinates: 50°57′00″N 104°13′00″W / 50.95°N 104.2167°W / 50.95; -104.2167CountryCanadaProvinceSaskatchewanCensus division6Rural MunicipalityCuparPost office established1903Incorporated (Village)1905Named forCuparGovernment • MayorValerie Orb • AdministratorSilvia Virgil...

Mansion in Manhattan, New York Not to be confused with the Edward S. Harkness House, also called the Harkness Mansion. The Nathaniel L. McCready House, also known as the Harkness Mansion, is a mansion at 4 East 75th Street on the Upper East Side of New York City. Completed in 1896 for Nathaniel L’Hommediue McCready Jr., during the twentieth century it was occupied by Thomas J. Watson, Rebekah Harkness, whose name became associated with the building when she used it as the offices of the Har...

2007 video game creation tool Platinum Arts SandboxDeveloper(s)Michael Tomaino, Kevin MeyerInitial releaseJune 4, 2007; 16 years ago (2007-06-04)Stable release2.8.2 / 19 January 2013; 11 years ago (2013-01-19) Operating systemMicrosoft Windows, Linux, FreeBSD, Mac OS XTypegame engine Platinum Arts Sandbox is a Video game programming tool. The tool was developed by Michael Tomaino and Kevin Meyer. Features in media PBS/WMHT Games in Education Conference [...

Gubernur Sulawesi TengahLambang Sulawesi TengahPetahanaRusdy Masturasejak 16 Juni 2021KediamanGubernuran SiranindiMasa jabatan5 tahunDibentuk13 April 1964; 60 tahun lalu (1964-04-13)Pejabat pertamaAnwar Datuk Madjo Basa Nan KuningSitus webSitus web resmi Gubernur Sulawesi Tengah adalah posisi tertinggi dalam pemerintahan provinsi Sulawesi Tengah. Dalam menjalankan roda pemerintahan daerah, Gubernur didampingi oleh Wakil Gubernur. Jabatan Gubernur Sulawesi Tengah saat ini dijabat ole...

Old Man & the GunRobert Redford in una scena del filmTitolo originaleThe Old Man & the Gun Lingua originaleinglese Paese di produzioneStati Uniti d'America Anno2018 Durata93 min Generebiografico, drammatico, poliziesco RegiaDavid Lowery SoggettoDavid Grann (articolo) SceneggiaturaDavid Lowery ProduttoreJames D. Stern, Dawn Ostroff, Jeremy Steckler, Robert Redford, Anthony Mastromauro, Toby Halbrooks, James Johnston, Bill Holderman Produttore esecutivoLucas Smith, Patrick Newal...

Batu Caves, salah satu ikon wisata di Malaysia Brickfields, India Kecil Kuala Lumpur [pranala nonaktif permanen]Menara Kembar Petronas Little India,Pulau Pinang , salah satu ikon wisata di Pulau Pinang [pranala nonaktif permanen]Dataran Tinggi Genting [pranala nonaktif permanen]Bukit Bintang [pranala nonaktif permanen]Gurney Drive Tempat wisata populer di Malaysia antara lain sebagai berikut: Tempat Ibadah Batu Caves Masjid Nasional Malaysia Masjid Negeri Sabah...

У этого термина существуют и другие значения, см. Западный округ. Западный внутригородской округ город Краснодар Дата основания 1936 год Дата упразднения 1994 Прежние имена Кагановичский, Ленинский районы Микрорайоны Дубинка, Черёмушки, Покровка Площадь 22[1] км² Насе...

Voce principale: L'Aquila Calcio. L'Aquila CalcioStagione 2000-2001Sport calcio Squadra L'Aquila Allenatore Paolo Stringara Presidente Michele Passarelli Serie C19ª Coppa Italia Serie CFase eliminatoria a gironi Miglior marcatoreCampionato: Di Nicola (17) 1999-2000 2001-2002 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti la società sportiva L'Aquila Calcio nelle competizioni ufficiali della stagione 2000-2001. Indice 1 Stagione 2 Divise e spon...

Questa voce o sezione sull'argomento elezioni non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Elezioni presidenziali negli Stati Uniti d'America del 1932 Stato Stati Uniti Data 8 novembre Collegio elettorale 531 elettori Affluenza 52,6% ( 4,3%) Candidati Franklin D. Roosevelt Herbert Hoover Partiti Democratico Repubblicano Voti 22 821 277...

منظمة الثورة الإسلامية في شبه الجزيرة العربية البلد السعودية تاريخ التأسيس 1979 تاريخ الحل 1991 المقر الرئيسي إيران الأيديولوجيا الشيعة تعديل مصدري - تعديل منظمة الثورة الإسلامية في شبه الجزيرة العربية هي حركة سياسية شيعية سعودية معارضة أسسها حسن الص...

淡江高峰塔倒塌事件高峰塔B座、C座公寓,與倒塌的A座公寓結構類似 (2012)日期1993年12月11日,30年前(1993-12-11)时间下午1时35分(马来西亚标准时间,周六)地点 马来西亚雪兰莪淡江(英语:Ulu Klang)山景花园(英语:Taman Hillview)高峰塔坐标3°10′33.4″N 101°45′42.1″E / 3.175944°N 101.761694°E / 3.175944; 101.761694坐标:3°10′33.4″N 101°45′42.1″E&...

Ion of fluorine This article is about the fluoride ion. For a review of fluorine compounds, see Compounds of fluorine. For the fluoride additive used in toothpaste, see Fluoride therapy. Not to be confused with Floride or Fluorite. Fluoride Names IUPAC name Fluoride[1] Identifiers CAS Number 16984-48-8 Y 3D model (JSmol) Interactive image ChEBI CHEBI:17051 ChEMBL ChEMBL1362 Y ChemSpider 26214 Y Gmelin Reference 14905 KEGG C00742 Y MeSH Fluoride PubChem CID 28179 UN...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Émilie DesjeuxÉmilie DesjeuxLahir(1861-10-09)9 Oktober 1861Meninggal23 April 1957KebangsaanPrancisPendidikanWilliam BouguereauTony Robert-FleuryPierre Victor Louis VignalDikenal atasPelukisPenghargaanOfficier d'académie[1] Émilie Desjeux (...

1898 Belgian general election ← 1896 22 May 1898 1900 → 75 of the 152 seats in the Chamber of Representatives First party Second party Leader Paul de Smet de Naeyer Grégoire Serwy Party Catholic Labour Seats won 36 15 Popular vote 377,275 213,511 Percentage 38.49% 21.78% Third party Fourth party Leader N/A Party Liberal Liberal–Socialist Seats won 12 8 Popular vote 177,802 91,947 Percentage 18.14% 9.38% Government befor...

Just for One Day (song) redirects here. For the song by The Grace, see Graceful 4. 2003 single by David Guetta vs. BowieJust for One Day (Heroes)Single by David Guetta vs. Bowiefrom the album Fuck Me I'm Famous 2003 Released16 June 2003Recorded2003GenreHousepop rockLength3:00LabelVirginSongwriter(s)David BowieProducer(s)David GuettaJoachim GarraudDavid Guetta singles chronology Give Me Something (2002) Just for One Day (Heroes) (2003) Money (2004) Just for One Day (Heroes) is a house song...

Pour les articles homonymes, voir Phèdre. PhèdrePhèdre et Hippolyte Édition Claude Barbin (1678). Auteur Jean Racine Genre Tragédie Nb. d'actes 5 actes en vers Durée approximative 3 h Sources Euripide Lieu de parution Paris Éditeur Jean Ribou Date de parution 1677 Date de création en français 1er janvier 1677 Lieu de création en français Paris Compagnie théâtrale Hôtel de Bourgogne Chronologie Iphigénie Esther modifier Phèdre est une tragédie en cinq actes et en vers d...