Hyperkähler manifold
|
Read other articles:

Iberdrola, S.A.JenisSociedad AnónimaKode emitenBMAD: IBEKomponen IBEX 35IndustriUtilitas listrikDidirikan1 November 1992KantorpusatBilbao, SpanyolTokohkunciJosé Ignacio Sánchez Galán (Ketua dan CEO)ProdukGenerasi dan distribusi listrik, energi terbaharui, produksi gas alam, penjualan dan distribusi, telekomunikasiPendapatan€31,64 miliar (2011)[1]Laba operasi€4,505 miliar (2011)[1]Laba bersih€2,804 miliar (2011)[1]Total aset€96,905 miliar (akhir 2011)&#...

Football leagueList of Italian football championsScudettoFounded1898CountryItalyConfederationUEFANumber of teams20Current championsNapoli(3rd title) (2022–23)Most championshipsJuventus(36 titles)Current: 2023–24 Serie A The Italian football champions (Italian: Campione d'Italia di calcio, plural: Campioni) are the annual winners of Serie A, Italy's premier football league competition. The title has been contested since 1898 in varying forms of competition. Napoli are the current champion...

Latter Day Saint teachings on race See also: Black people and Mormonism, Native American people and Mormonism, and Interracial marriage and the LDS Church Part of a series on theBook of Mormon Origin Cumorah Golden plates Joseph Smith Emma Smith Oliver Cowdery Sidney Rigdon David Whitmer Martin Harris Lucy Harris Book of Mormon witnesses Three Witnesses Eight Witnesses Spalding–Rigdon theory Peoples Jaredites Nephites Amalekites Amlicites Zoramites Lamanites Lemuelites Anti-Nephi-Lehies Amu...

التَرْتِيبِ الإداري في جُمهُوريَّة ألمانيا الاِتّحاديّة منطقة إدارية ألمانية (بالألمانية: Regierungsbezirk)، وهو تقسيم لبعض الولايات الاتحادية (Bundesländer) يرادفه مصطلح «محافظة» في بعد الدول العربية.[1] والمناطق الإدارية تقسم هي الأخرى إلى أقضية (kreise) وتكون إما أقضية ريفية (landkreise...

Book by Nerida Newton This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Lambing Flat – news · newspapers · books · scholar · JSTOR (May 2019) (Learn how and when to remove this template message) The Lambing Flat First edition coverAuthorNerida NewtonCountryAustraliaLanguageEnglishGenreHistorical novelPublisherUniversity of ...

Struktur kimia dasar dari antosianin. Antosianin (bahasa Inggris: anthocyanin, dari gabungan kata Yunani: anthos = bunga, dan cyanos = biru) adalah pigmen yang larut di air yang secara alami terdapat pada berbagai jenis tumbuhan.[1] Sesuai namanya, pigmen ini memberikan warna pada bunga, buah, dan daun tumbuhan hijau,[1] dan telah banyak digunakan sebagai pewarna alami pada berbagai produk pangan dan berbagai aplikasi lainnya.[1] Warna diberikan oleh antosianin berkat ...

Clévillecomune Cléville – Veduta LocalizzazioneStato Francia Regione Normandia Dipartimento Calvados ArrondissementCaen CantoneTroarn TerritorioCoordinate49°09′N 0°06′W / 49.15°N 0.1°W49.15; -0.1 (Cléville)Coordinate: 49°09′N 0°06′W / 49.15°N 0.1°W49.15; -0.1 (Cléville) Superficie8,51 km² Abitanti350[1] (2009) Densità41,13 ab./km² Altre informazioniCod. postale14370 Fuso orarioUTC+1 Codice INSEE14163 Carto...

Swedish multinational manufacturing company This article is about the Volvo Group (AB Volvo). For the separate manufacturer of passenger automobiles, see Volvo Cars. For other uses, see Volvo (disambiguation). AB VolvoCompany typeAktiebolagTraded asNasdaq Stockholm: VOLV A, Nasdaq Stockholm: VOLV BISINSE0000115446IndustryAutomotiveFounded1927; 97 years ago (1927)FoundersAssar Gabrielsson and Gustav LarsonHeadquartersGothenburg, SwedenArea servedWorldwideKey peopleC...
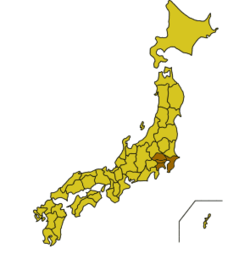
Bendera Tokyo Peta Jepang dengan wilayah metropolitan Tokyo Raya ditandai. Tokyo Raya adalah sebuah wilayah metropolitan di Jepang yang terdiri dari sebagian besar Chiba, Kanagawa, Saitama, dan Tokyo. Dalam bahasa Jepang, wilayah ini disebut Wilayah Tokyo (東京圏code: ja is deprecated , Tōkyō-ken), Wilayah Ibu Kota (首都圏code: ja is deprecated , Shuto-ken) atau Kanto Selatan (南関東code: ja is deprecated , Minami-Kantō). Tokyo Raya adalah wilayah metropolitan terbesar di dunia (3...

American book review magazine Kirkus redirects here. For the surname, see Kirkus (surname). Kirkus ReviewsEditorVirginia Kirkus (1933 – July 1962)CategoriesBook reviewsFrequencySemimonthlyPublisherVirginia Kirkus Bookshop Service, Virginia Kirkus Service, Inc. (from 1962), and others Kirkus Media, LLC (from 2010)First issueJanuary 1933; 91 years ago (1933-01)CountryUnited StatesBased inNew York City, New York, U.S.LanguageEnglishWebsitekirkusreviews.comISSN1948-7428 K...

La famille Jackson est une famille américaine de chanteurs et de musiciens — œuvrant en solo ou en groupe (Jackson Five, 3T) —, originaire de Gary dans l'Indiana (près de Chicago), et qui s'installe, dans les années 1970, à Encino, un quartier de Los Angeles en Californie. Le membre le plus célèbre de cette famille est le chanteur et auteur-compositeur-interprète Michael Jackson (1958-2009), qui, après avoir été membre des Jackson Five, connaît une carrière solo int...

Central business district and residential area in Texas, United StatesDallas Central Business DistrictCentral business district and residential areaDowntown DallasSkyline of Downtown Dallas seen from Reunion TowerNickname: Big DLocation in DallasCountry United StatesState TexasCounties DallasCity DallasArea • Total3.63 km2 (1.4 sq mi) • Land3.63 km2 (1.4 sq mi) • Water0 km2 (0 sq mi) 0%Eleva...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Slatina, Rumania – berita · surat kabar · buku · cendekiawan · JSTOR SlatinaKota Lambang kebesaranNegara RumaniaCountyCounty OltStatusIbukota CountyPemerintahan • Wali kotaMinel Prina (S...

У этого термина существуют и другие значения, см. Ясный (значения). Космодром Ясный Космодром Ясный. Общий вид. Расположение Россия Руководящий орган Министерство обороны Российской Федерации Космодром Ясный Медиафайлы на Викискладе Ясный — российский космодр�...

Dalam kimia organik, reaksi elektrosiklik adalah suatu reaksi interkonversi bersama dari sistem elektron π terkonjugasi dengan mengubah satu ikatan π menjadi cincin yang membentuk ikatan σ. Pada umumnya, reaksi elektrosiklik termasuk reaksi bolak-balik dimana arah reaksi bergantung pada stabilitas termodinamika produk.[1] Penggunaan termal atau fotokimia akan menentukan produk dari reaksi, sebagai contoh bila suatu reaktan heksadiena disinari oleh cahaya ultraviolet, maka akan terb...

United KingdomMinister of State for Defence ProcurementRoyal Arms of His Majesty's GovernmentIncumbentJames Cartlidgesince 21 April 2023Ministry of DefenceStyleMinisterNominatorPrime Minister of the United KingdomAppointerThe Monarchon advice of the Prime MinisterTerm lengthAt His Majesty's pleasureFirst holderRoy MasonWebsiteOfficial website The Minister of State for Defence Procurement is, as a Minister of State, a mid-level defence minister in the Ministry of Defence of the British Go...

Pour les articles homonymes, voir Bélanger. Ne doit pas être confondu avec Paul Béranger. Paul BélangerBiographieNaissance 1953LévisNationalité canadienneActivités Poète, écrivain, éditeurAutres informationsA travaillé pour Éditions du NoroîtUniversité du Québec à MontréalGenre artistique PoésieDistinctions Prix Alain-Grandbois (2010)Prix de poésie Gatien Lapointe - Jaime-Sabines (2018)modifier - modifier le code - modifier Wikidata Paul Bélanger est un poète et éditeur...

Hukuman Iksion; Nefele duduk di kaki Merkurius (Hermes). Lukisan dinding Romawi di Pompeii. Dalam mitologi Yunani, Nefele (bahasa Yunani: Νεφέλη, dari νέφος nephos awan) adalah nimfa atau dewi awan. Nefele merupakan tokoh penting dalam kisah Friksos dan Helle.[1] Zeus menciptakan Nefele dari awan dalam wujud yang menyerupai Hera. Zeus menciptakan Nefele untuk menguji Iksion, yang dicurigai oleh Zeus berhasrat pada Hera. Iksion melihat Nefele dan mengiranya sebagai Hera....

Local government elections in Greater Manchester, England Rochdale Metropolitan Borough Council elections are generally held three years out of every four, with a third of the council being elected each time. Rochdale Metropolitan Borough Council, generally known as Rochdale Borough Council, is the local authority for the metropolitan borough of Rochdale in Greater Manchester, England. Since the last boundary changes in 2022, 60 councillors have been elected from 20 wards.[1] Council ...




























