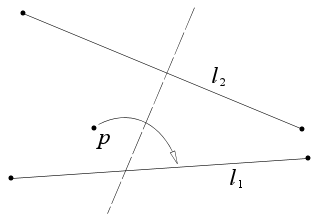
Huzita–Hatori axioms
|
Read other articles:

Jaqueline Vargas é uma autora de telenovelas brasileiras, conhecida por seu trabalho na bem-sucedida Floribella.[1][2][3] Também foi responsável pela adaptação da série israelense Be tipul - Sessão de Terapia para o Brasil. A série originalmente com duas temporadas, teve uma terceira temporada original criada pela autora. Trabalhou no SBT em 2009, na qual foi co-autora da novela Vende-se um Véu de Noiva. Em 2015 foi co-autora da décima quinta temporada de Malhação, Malhação: Mú...

Ricardo La Volpe Informasi pribadiNama lengkap Ricardo Antonio La Volpe GuarchoniTanggal lahir 6 Februari 1952 (umur 72)Tempat lahir Buenos Aires, ArgentinaTinggi 1,88 m (6 ft 2 in)Posisi bermain Penjaga gawangKarier senior*Tahun Tim Tampil (Gol)1971–1975 Banfield 108 (0)1975–1979 San Lorenzo 112 (0)1979–1982 Atlante 1982–1983 Oaxtepec Tim nasional1975-1978 Argentina 8 (0)Kepelatihan1983–1984 Oaxtepec1988–1989 Atlante1989 Guadalajara1990–1991 Querétaro1991�...

كأس فنلندا 2012 تفاصيل الموسم كأس فنلندا النسخة 58 البلد فنلندا التاريخ بداية:6 يناير 2012 نهاية:29 سبتمبر 2012 المنظم اتحاد فنلندا لكرة القدم البطل هونكا عدد المشاركين 198 كأس فنلندا 2011 كأس فنلندا 2013 تعديل مصدري - تعديل كأس فنلندا 2012 (بالفنلندية:...

Public school in Texas, United States A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (December 2012) (Learn how and when to remove this template message) Victory Early College High SchoolLocationCoordinates29°52′05″N 95°27′58″W / 29.868082°N 95.466133°W / 29.868082; -95.466...

Location of Tioga County in New York Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) List of the National Register of Historic Places listings in Tioga County, New York This is intended to be a complete list of properties and districts listed on the National Register of Historic Places in Tioga County, New York. The locations of National Register properties and districts (at least for all showing...

Protein-coding gene in the species Homo sapiens RRM2BAvailable structuresPDBOrtholog search: PDBe RCSB List of PDB id codes2VUX, 3HF1, 4DJNIdentifiersAliasesRRM2B, MTDPS8A, MTDPS8B, P53R2, ribonucleotide reductase regulatory TP53 inducible subunit M2B, RCDFRDExternal IDsOMIM: 604712 MGI: 2155865 HomoloGene: 56723 GeneCards: RRM2B Gene location (Human)Chr.Chromosome 8 (human)[1]Band8q22.3Start102,204,502 bp[1]End102,238,961 bp[1]Gene location (Mouse)Chr.Chromosome 15 (m...

Avenue in Munich, Germany View to the south. Left: St. Theresia; in the back: Central Tower Munich The Landshuter Allee is an avenue in Munich and through most of its course it is part of the Mittlerer Ring, the Bundesstraße 2 R. It joins Donnersbergerbrücke at Arnulfstraße in the Neuhausen district and runs from Dachauer Straße west of the Olympiapark to Moosacher Straße west of the Olympic village in the Moosach district. The B 2R leaves the intersection-free avenue at the Landshuter A...

1927 film Tea for ThreeLobby cardDirected byRobert Z. LeonardScreenplay byGarrett GrahamF. Hugh HerbertRoi Cooper MegrueLucille NewmarkStarringLew CodyAileen PringleOwen MooreCinematographyAndré Barlatier -(French Wikipedia)Edited byWilliam LeVanwayProductioncompanyMetro-Goldwyn-MayerDistributed byMetro-Goldwyn-MayerRelease date October 29, 1927 (1927-10-29) Running time70 minutesCountryUnited StatesLanguageEnglish Tea for Three is a lost[1][2] 1927 American co...

Disambiguazione – Se stai cercando altri significati, vedi Polack (disambigua) o Polock (disambigua). Questa voce sull'argomento centri abitati della Bielorussia è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Polackcittà(BE) Полацк(RU) Полоцк Polack – Veduta LocalizzazioneStato Bielorussia RegioneVicebsk DistrettoPolack AmministrazioneSindacoNikolaj Ševčuk TerritorioCoordinate55°29′31.5″N 28°48′04.85″E / ...

Telugu cinema (Tollywood) 1930s 1940s 1941 1942 1943 19441945 1946 1947 1948 1949 1950 1950s 1951 1952 1953 19541955 1956 1957 1958 1959 1960 1960s 1961 1962 1963 19641965 1966 1967 1968 1969 1970 1970s 1971 1972 1973 19741975 1976 1977 1978 1979 1980 1980s 1981 1982 1983 19841985 1986 1987 1988 1989 1990 1990s 1991 1992 1993 19941995 1996 1997 1998 1999 2000 2000s 2001 2002 2003 20042005 2006 2007 2008 2009 2010 2010s 2011 2012 2013 20142015 2016 2017 2018 2019 2020 2020s 2021 2022 2023 202...

ميغا مان 2 (باليابانية: ロックマン2 Dr.ワイリーの謎)، و(بالإنجليزية: Mega Man 2)[1] غلاف اللعبة في أمريكا الشمالية المطور كابكوم الناشر كابكوم الموزع نينتندو إي شوب، وجوجل بلاي، وآب ستور المخرج أكيرا كيتامورا المبرمج نوبويوكي ماتسوشيما المنتج توكورو فوجيوارا ا�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2021) كان رد الفعل الدولي على كارثة فوكوشيما دايشي النووية عام 2011 متنوعًا وواسع الانتشار. استجابت العديد من الوكالات الحكومية الدولية لكارثة فوكوشيما دايشي النو...

County in Ireland Carlow County redirects here. For other uses, see Carlow (disambiguation). County in Leinster, IrelandCounty Carlow Contae CheatharlachCounty Coat of armsNicknames: The Dolmen County (Others)Anthem: Follow Me up to CarlowCountryIrelandProvinceLeinsterRegionSouthernEstablished1210[1]County townCarlowGovernment • Local authorityCarlow County Council • Dáil constituencyCarlow–Kilkenny • EP constituencySouthArea • T...

Israel-based Zionist non-governmental organization Im TirtzuFounded2006; 18 years ago (2006)[1]TypeNon-governmental organizationRegistration no.580471662[2]Area served IsraelKey peopleRonen Shoval (Founder)[3] Matan Peleg (CEO)[4]Websitehttps://imti.org.il/en Im Tirtzu (Hebrew: אם תרצו, lit. 'If you will it') is a Zionist[6][7] non-governmental organization based in Israel.[1] Its name is derived from an epig...

American journalist George Bubb Dangerfield (28 October 1904 in Newbury, Berkshire – 27 December 1986 in Santa Barbara, California) was a British-born American journalist, historian, and the literary editor of Vanity Fair from 1933 to 1935. He is known primarily for his book The Strange Death of Liberal England (1935), a classic account of how the Liberal Party in Great Britain ruined itself in dealing with the House of Lords, women's suffrage, the Irish question, and labour unions, 1906–...

The Hallowell family is an American family from Philadelphia and Boston, notable for their activism in the abolitionist movement and for their philanthropy to various universities and civil rights organizations.[1][2][3] The Hallowell family is frequently associated with Boston Brahmins.[4][5] Notable members John Singleton Copley, Benjamin Hallowell, Jr. 1764Gilbert Stuart, Ward Nicholas Boylston, 1825, Museum of Fine Arts 17th century Benjamin Hallowe...
Predicting the future of technology Futures studies Concepts Accelerating change Cashless society Existential risk Future Earth Mathematics Race Climate Space exploration Universe Historical materialism Kondratiev cycle Kardashev scale Moore's law Peak oil Population cycle Resource depletion Singularity Swanson's law Techniques Backcasting Causal layered analysis Chain-linked model Consensus forecast Cross impact analysis Delphi Real-time Delphi Foresight Future-proof Futures wheel Futures wo...

بيشباغير الإحداثيات 45°02′00″N 42°38′00″E / 45.03333333°N 42.63333333°E / 45.03333333; 42.63333333 تقسيم إداري البلد روسيا تعديل مصدري - تعديل يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة �...

Abd as-Salam Arif Nama dalam bahasa asli(ar) عبد السلام عارف BiografiKelahiran21 Maret 1921 Bagdad Kematian13 April 1966 (45 tahun)Sungai Shatt al-Arab, dekat Penyebab kematianKecelakaan pesawat terbang 2 Daftar Presiden Irak 8 Februari 1963 – 13 April 1966 ← Muhammad Najib ar-Ruba'i – Abdul Rahman Arif → Data pribadiAgamaIslam Sunni KegiatanPekerjaanpolitikus, personel militer Partai politikPartai Ba'th Sosialis Arab – Wilayah Irak Cabang mil...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (January 2024) (Learn how and when to remove this message) W.27 and W.32 Hansa-Brandenburg W.27 Role Fighter floatplaneType of aircraft National origin Germany Manufacturer Hansa-Brandenburg Number built 2 The Hansa Brandenburg W.27 and W.32 were prototype fighter floatplanes de...
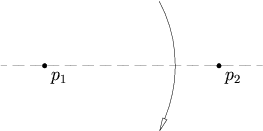











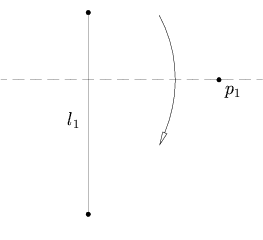

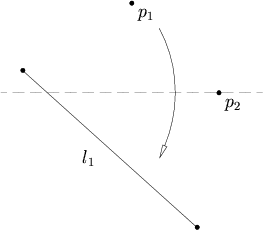












![{\displaystyle {\begin{aligned}F_{1}(s)&=p_{1}+{\frac {1}{2}}(d_{1}-p_{1})+s(d_{1}-p_{1})^{\perp }\\[8pt]F_{2}(s)&=p_{1}+{\frac {1}{2}}(d_{2}-p_{1})+s(d_{2}-p_{1})^{\perp }.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a48e70d1a14331f3013f2e5a17da2fd2f29c28d6)