Hughes–Drever experiment

7Li NMR spectrum of LiCl (1M) in D2O. The sharp, unsplit NMR line of this isotope of lithium is evidence for the isotropy of mass and space.

Hughes–Drever experiments (also clock comparison-, clock anisotropy-, mass isotropy-, or energy isotropy experiments) are spectroscopic tests of the isotropy of mass and space. Although originally conceived of as a test of Mach's principle, they are now understood to be an important test of Lorentz invariance. As in Michelson–Morley experiments, the existence of a preferred frame of reference or other deviations from Lorentz invariance can be tested, which also affects the validity of the equivalence principle. Thus these experiments concern fundamental aspects of both special and general relativity. Unlike Michelson–Morley type experiments, Hughes–Drever experiments test the isotropy of the interactions of matter itself, that is, of protons, neutrons, and electrons. The accuracy achieved makes this kind of experiment one of the most accurate confirmations of relativity (see also Tests of special relativity).[A 1][A 2][A 3][A 4][A 5][A 6]

Experiments by Hughes and Drever

Giuseppe Cocconi and Edwin Ernest Salpeter (1958) theorized that inertia depends on the surrounding masses according to Mach's principle. Nonuniform distribution of matter thus would lead to anisotropy of inertia in different directions. Heuristic arguments led them to believe that any inertial anisotropy, if one existed, would be dominated by mass contributions from the center of our Milky Way galaxy. They argued that this anisotropy might be observed in two ways: measuring the Zeeman splitting in an atom[1] or measuring the Zeeman splitting in the excited nuclear state of 57
Fe
 using the Mössbauer effect.[2]

Vernon W. Hughes et al. (1960)[3] and Ronald Drever (1961)[4] independently conducted similar spectroscopic experiments to test Mach's principle. However, they didn't use the Mössbauer effect but made magnetic resonance measurements of the nucleus of lithium-7, whose ground state possesses a spin of 3⁄2. The ground state is split into four equally spaced magnetic energy levels when measured in a magnetic field in accordance with its allowed magnetic quantum number. The nuclear wave functions for the different energy levels have different spatial distributions relative to the magnetic field, and thus have different directional properties. If mass isotropy is satisfied, each transition between a pair of adjacent levels should emit a photon of equal frequency, resulting in a single, sharp spectral line. On the other hand, if inertia has a directional dependence, a triplet or broadened resonance line should be observed. During the 24-hour course of Drever's version of the experiment, the Earth turned, and the magnetic field axis swept different sections of the sky. Drever paid particular attention to the behavior of the spectral line as the magnetic field crossed the center of the galaxy.[A 7] Neither Hughes nor Drever observed any frequency shift of the energy levels, and due to their experiments' high precision, the maximal anisotropy could be limited to 0.04 Hz = 10−25 GeV.

Regarding the consequences of the null result for Mach's principle, it was shown by Robert H. Dicke (1961) that it is in agreement with this principle, as long as the spatial anisotropy is the same for all particles. Thus the null result is rather showing that inertial anisotropy effects are, if they exist, universal for all particles and locally unobservable.[5][6]

Modern interpretation

While the motivation for this experiment was to test Mach's principle, it has since become recognized as an important test of Lorentz invariance and thus special relativity. This is because anisotropy effects also occur in the presence of a preferred and Lorentz-violating frame of reference – usually identified with the CMBR rest frame as some sort of luminiferous aether (relative velocity about 368 km/s). Therefore, the negative results of the Hughes–Drever experiments (as well as the Michelson–Morley experiments) rule out the existence of such a frame. In particular, Hughes–Drever tests of Lorentz violations are often described by a test theory of special relativity put forward by Clifford Will. According to this model, Lorentz violations in the presence of preferred frames can lead to differences between the maximal attainable velocity of massive particles and the speed of light. If they were different, the properties and frequencies of matter interactions would change as well. In addition, it is a fundamental consequence of the equivalence principle of general relativity that Lorentz invariance locally holds in freely moving reference frames = local Lorentz invariance (LLI). This means that the results of this experiment concern both special and general relativity.[A 1][A 2]

Due to the fact that different frequencies ("clocks") are compared, these experiments are also denoted as clock-comparison experiments.[A 3][A 4]

Recent experiments

Further information: Modern searches for Lorentz violation

Besides Lorentz violations due to a preferred frame or influences based on Mach's principle, spontaneous violations of Lorentz invariance and CPT symmetry are also being searched for, motivated by the predictions of various quantum gravity models that suggest their existence. Modern updates of the Hughes–Drever experiments have been conducted studying possible Lorentz and CPT violation in neutrons and protons. Using spin-polarized systems and co-magnetometers (to suppress magnetic influences), the accuracy and sensitivity of these experiments have been greatly increased. In addition, by using spin-polarized torsion balances, the electron sector has also been tested.[A 5][A 6]

All of these experiments have thus far given negative results, so there is still no sign of the existence of a preferred frame or any other form of Lorentz violation. The values of the following table are related to the coefficients given by the Standard-Model Extension (SME), an often used effective field theory to assess possible Lorentz violations (see also other Test theories of special relativity). From that, any deviation of Lorentz invariance can be connected with specific coefficients. Since a series of coefficients are tested in those experiments, only the value of maximal sensitivity is given (for precise data, see the individual articles):[A 3][A 8][A 4]

Author Year SME constraints Description
Proton Neutron Electron
Prestage et al.[7] 1985 10−27 Comparing the nuclear spin-flip transition of 9
Be+
 (stored in a penning trap) with a hydrogen maser transition.
Phillips[8] 1987 10−27 Sinusoidal oscillations were investigated using a cryogenic spin-torsion pendulum carrying a transversely polarized magnet.
Lamoreaux et al.[9] 1989 10−29 They induced dipole and quadrupole spin polarization into a vapor of 201
Hg
, by which quadrupole energy shifts can be observed.
Chupp et al.[10] 1989 10−27 Time-dependent quadrupole splitting of Zeeman levels is investigated. 21
Ne
 and 3
He
 gases are polarized by spin exchange and compared.
Wineland et al.[11] 1991 10−25 The anomalous dipole-monopole and dipole-dipole couplings are investigated, by examining hyperfine resonances in 9
Be+
.
Wang et al.[12] 1993 10−27 A spin-torsion pendulum carrying a spin-polarized Dy–Fe mass is investigated for sidereal variations.
Berglund et al.[13] 1995 10−27 10−30 10−27 The frequencies of 199Hg and 133Cs are compared by applying a magnetic field.
Bear et al.[14] 2000 10−31 The frequencies of 129
Xe
 and 3
He
 Zeeman masers are compared.
Phillips et al.[15] 2000 10−27 The Zeeman frequency is measured using hydrogen masers.
Humphrey et al.[16] 2003 10−27 10−27 Similar to Phillips et al. (2000).
Hou et al.[17] 2003 10−29 Similar to Wang et al. (1993).
Canè et al.[18] 2004 10−32 Similar to Bear et al. (2000).
Wolf et al.[19] 2006 10−25 Atomic frequencies are measured using laser cooled 133
Cs
 atomic fountains.
Heckel et al.[20] 2006 10−30 They used a spin-torsion pendulum with four sections of Alnico and four sections of Sm5Co.
Heckel et al.[21] 2008 10−31 Similar to Heckel et al. (2006).
Altarev et al.[22] 2009 10−29 The spin-precession frequencies in stored ultracold neutrons and 199
Hg
 are analyzed.
Brown et al.[23] 2010 10−32 10−33 Comparing the frequencies in a K / 3
He
 comagnetometer.
Gemmel et al.[24] 2010 10−32 Comparing the frequencies in a 129
Xe
 / 3
He
 comagnetometer.
Smiciklas et al.[25] 2011 10−29 Comparing the frequencies in a 21
Ne
 / Rb / K comagnetometer. Test of the maximal attainable velocity of neutrons.
Peck et al.[26] 2012 10−30 10−31 Similar to Berglund et al. (1995).
Hohensee et al.[27] 2013 10−17 Measuring the transition frequencies of two nearly degenerate states of 164
Dy
 and 162
Dy
. Test of the maximal attainable velocity of electrons.
Allmendinger et al.[28] 2013 10−34 Similar to Gemmel et al. (2010).

Secondary sources

  1. ^ a b Will, C. M. (2006). "The Confrontation between General Relativity and Experiment". Living Reviews in Relativity. 9 (3): 3. arXiv:gr-qc/0510072. Bibcode:2006LRR.....9....3W. doi:10.12942/lrr-2006-3. PMC 5256066. PMID 28179873.
  2. ^ a b Will, C. M. (1995). "Stable clocks and general relativity". Proceedings of the 30th Rencontres de Moriond: 417. arXiv:gr-qc/9504017. Bibcode:1995dmcc.conf..417W.
  3. ^ a b c Kostelecký, V. Alan; Lane, Charles D. (1999). "Constraints on Lorentz violation from clock-comparison experiments". Physical Review D. 60 (11): 116010. arXiv:hep-ph/9908504. Bibcode:1999PhRvD..60k6010K. doi:10.1103/PhysRevD.60.116010. S2CID 119039071.
  4. ^ a b c Mattingly, David (2005). "Modern Tests of Lorentz Invariance". Living Rev. Relativ. 8 (5): 5. arXiv:gr-qc/0502097. Bibcode:2005LRR.....8....5M. doi:10.12942/lrr-2005-5. PMC 5253993. PMID 28163649.
  5. ^ a b Pospelov, Maxim; Romalis, Michael (2004). "Lorentz Invariance on Trial" (PDF). Physics Today. 57 (7): 40–46. Bibcode:2004PhT....57g..40P. doi:10.1063/1.1784301. Archived from the original (PDF) on 2022-01-02. Retrieved 2011-05-26.
  6. ^ a b Walsworth, R. L. (2006). "Tests of Lorentz Symmetry in the Spin-Coupling Sector" (PDF). Special Relativity. Lecture Notes in Physics. Vol. 702. pp. 493–505. doi:10.1007/3-540-34523-X_18. ISBN 978-3-540-34522-0.
  7. ^ Bartusiak, Marcia (2003). Einstein's Unfinished Symphony: Listening to the Sounds of Space-Time. Joseph Henry Press. pp. 96–97. ISBN 0425186202. Retrieved 15 Jul 2012. 'I watched that line over a 24-hour period as the Earth rotated. As the axis of the field swung past the center of the galaxy and other directions, I looked for a change,' recalls Drever.
  8. ^ Hou, Li-Shing; Ni, Wei-Tou; Li, Yu-Chu M. (2003). "Test of Cosmic Spatial Isotropy for Polarized Electrons Using a Rotatable Torsion Balance". Physical Review Letters. 90 (20): 201101. arXiv:physics/0009012. Bibcode:2003PhRvL..90t1101H. doi:10.1103/PhysRevLett.90.201101. PMID 12785879. S2CID 28211115.

Primary sources

  1. ^ Cocconi, G.; Salpeter E. (1958). "A search for anisotropy of inertia". Il Nuovo Cimento. 10 (4): 646–651. Bibcode:1958NCim...10..646C. doi:10.1007/BF02859800. S2CID 123226805.
  2. ^ Cocconi, G.; Salpeter E. (1960). "Upper Limit for the Anisotropy of Inertia from the Mössbauer Effect". Physical Review Letters. 4 (4): 176–177. Bibcode:1960PhRvL...4..176C. doi:10.1103/PhysRevLett.4.176.
  3. ^ Hughes, V. W.; Robinson, H. G.; Beltran-Lopez, V. (1960). "Upper Limit for the Anisotropy of Inertial Mass from Nuclear Resonance Experiments". Physical Review Letters. 4 (7): 342–344. Bibcode:1960PhRvL...4..342H. doi:10.1103/PhysRevLett.4.342.
  4. ^ Drever, R. W. P. (1961). "A search for anisotropy of inertial mass using a free precession technique". Philosophical Magazine. 6 (65): 683–687. Bibcode:1961PMag....6..683D. doi:10.1080/14786436108244418.
  5. ^ Dicke, R. H. (1961). "Experimental Tests of Mach's Principle". Physical Review Letters. 7 (9): 359–360. Bibcode:1961PhRvL...7..359D. doi:10.1103/PhysRevLett.7.359.
  6. ^ Dicke, R. H. (1964). The Theoretical Significance of Experimental Relativity. Gordon and Breach.
  7. ^ Prestage, J. D.; Bollinger, J. J.; Itano, W. M.; Wineland, D. J. (1985). "Limits for spatial anisotropy by use of nuclear-spin-polarized Be-9(+) ions". Physical Review Letters. 54 (22): 2387–2390. Bibcode:1985PhRvL..54.2387P. doi:10.1103/PhysRevLett.54.2387. PMID 10031329.
  8. ^ Phillips, P. R. (1987). "Test of spatial isotropy using a cryogenic spin-torsion pendulum". Physical Review Letters. 59 (5): 1784–1787. Bibcode:1987PhRvL..59.1784P. doi:10.1103/PhysRevLett.59.1784. PMID 10035328.
  9. ^ Lamoreaux, S. K.; Jacobs, J. P.; Heckel, B. R.; Raab, F. J.; Fortson, E. N. (1989). "Optical pumping technique for measuring small nuclear quadrupole shifts in 1S(0) atoms and testing spatial isotropy". Physical Review A. 39 (3): 1082–1111. Bibcode:1989PhRvA..39.1082L. doi:10.1103/PhysRevA.39.1082. PMID 9901347.
  10. ^ Chupp, T. E.; Hoare, R. J.; Loveman, R. A.; Oteiza, E. R.; Richardson, J. M.; Wagshul, M. E.; Thompson, A. K. (1989). "Results of a new test of local Lorentz invariance: A search for mass anisotropy in 21Ne". Physical Review Letters. 63 (15): 1541–1545. Bibcode:1989PhRvL..63.1541C. doi:10.1103/PhysRevLett.63.1541. PMID 10040606.
  11. ^ Wineland, D. J.; Bollinger, J. J.; Heinzen, D. J.; Itano, W. M.; Raizen, M. G. (1991). "Search for anomalous spin-dependent forces using stored-ion spectroscopy". Physical Review Letters. 67 (13): 1735–1738. Bibcode:1991PhRvL..67.1735W. doi:10.1103/PhysRevLett.67.1735. PMID 10044234.
  12. ^ Wang, Shih-Liang; Ni, Wei-Tou; Pan, Sheau-Shi (1993). "New Experimental Limit on the Spatial Anisotropy for Polarized Electrons". Modern Physics Letters A. 8 (39): 3715–3725. Bibcode:1993MPLA....8.3715W. doi:10.1142/S0217732393003445.
  13. ^ Berglund, C. J.; Hunter, L. R.; Krause, D. Jr.; Prigge, E. O.; Ronfeldt, M. S.; Lamoreaux, S. K. (1995). "New Limits on Local Lorentz Invariance from Hg and Cs Magnetometers". Physical Review Letters. 75 (10): 1879–1882. Bibcode:1995PhRvL..75.1879B. doi:10.1103/PhysRevLett.75.1879. PMID 10059152.
  14. ^ Bear, D.; Stoner, R. E.; Walsworth, R. L.; Kostelecký, V. Alan; Lane, Charles D. (2000). "Limit on Lorentz and CPT Violation of the Neutron Using a Two-Species Noble-Gas Maser". Physical Review Letters. 85 (24): 5038–5041. arXiv:physics/0007049. Bibcode:2000PhRvL..85.5038B. doi:10.1103/PhysRevLett.85.5038. PMID 11102181. S2CID 41363493.
  15. ^ Phillips, D. F.; Humphrey, M. A.; Mattison, E. M.; Stoner, R. E.; Vessot, R. F.; Walsworth, R. L. (2001). "Limit on Lorentz and CPT violation of the proton using a hydrogen maser". Physical Review D. 63 (11): 111101. arXiv:physics/0008230. Bibcode:2001PhRvD..63k1101P. doi:10.1103/PhysRevD.63.111101. S2CID 10665017.
  16. ^ Humphrey, M. A.; Phillips, D. F.; Mattison, E. M.; Vessot, R. F.; Stoner, R. E.; Walsworth, R. L. (2003). "Testing CPT and Lorentz symmetry with hydrogen masers". Physical Review A. 68 (6): 063807. arXiv:physics/0103068. Bibcode:2003PhRvA..68f3807H. doi:10.1103/PhysRevA.68.063807. S2CID 13659676.
  17. ^ Hou, Li-Shing; Ni, Wei-Tou; Li, Yu-Chu M. (2003). "Test of Cosmic Spatial Isotropy for Polarized Electrons Using a Rotatable Torsion Balance". Physical Review Letters. 90 (20): 201101. arXiv:physics/0009012. Bibcode:2003PhRvL..90t1101H. doi:10.1103/PhysRevLett.90.201101. PMID 12785879. S2CID 28211115.
  18. ^ Canè, F.; Bear, D.; Phillips, D. F.; Rosen, M. S.; Smallwood, C. L.; Stoner, R. E.; Walsworth, R. L.; Kostelecký, V. Alan (2004). "Bound on Lorentz and CPT Violating Boost Effects for the Neutron". Physical Review Letters. 93 (23): 230801. arXiv:physics/0309070. Bibcode:2004PhRvL..93w0801C. doi:10.1103/PhysRevLett.93.230801. PMID 15601138. S2CID 20974775.
  19. ^ Wolf, P.; Chapelet, F.; Bize, S.; Clairon, A. (2006). "Cold Atom Clock Test of Lorentz Invariance in the Matter Sector". Physical Review Letters. 96 (6): 060801. arXiv:hep-ph/0601024. Bibcode:2006PhRvL..96f0801W. doi:10.1103/PhysRevLett.96.060801. PMID 16605978. S2CID 141060.
  20. ^ Heckel, B. R.; Cramer, C. E.; Cook, T. S.; Adelberger, E. G.; Schlamminger, S.; Schmidt, U. (2006). "New CP-Violation and Preferred-Frame Tests with Polarized Electrons". Physical Review Letters. 97 (2): 021603. arXiv:hep-ph/0606218. Bibcode:2006PhRvL..97b1603H. doi:10.1103/PhysRevLett.97.021603. PMID 16907432. S2CID 27027816.
  21. ^ Heckel, B. R.; Adelberger, E. G.; Cramer, C. E.; Cook, T. S.; Schlamminger, S.; Schmidt, U. (2008). "Preferred-frame and CP-violation tests with polarized electrons". Physical Review D. 78 (9): 092006. arXiv:0808.2673. Bibcode:2008PhRvD..78i2006H. doi:10.1103/PhysRevD.78.092006. S2CID 119259958.
  22. ^ Altarev, I.; et al. (2009). "Test of Lorentz Invariance with Spin Precession of Ultracold Neutrons". Physical Review Letters. 103 (8): 081602. arXiv:0905.3221. Bibcode:2009PhRvL.103h1602A. doi:10.1103/PhysRevLett.103.081602. PMID 19792714. S2CID 5224718.
  23. ^ Brown, J. M.; Smullin, S. J.; Kornack, T. W.; Romalis, M. V. (2010). "New Limit on Lorentz- and CPT-Violating Neutron Spin Interactions". Physical Review Letters. 105 (15): 151604. arXiv:1006.5425. Bibcode:2010PhRvL.105o1604B. doi:10.1103/PhysRevLett.105.151604. PMID 21230893. S2CID 4187692.
  24. ^ Gemmel, C.; Heil, W.; Karpuk, S.; Lenz, K.; Sobolev, Yu.; Tullney, K.; Burghoff, M.; Kilian, W.; Knappe-Grüneberg, S.; Müller, W.; Schnabel, A.; Seifert, F.; Trahms, L.; Schmidt, U. (2010). "Limit on Lorentz and CPT violation of the bound neutron using a free precession He3/Xe129 comagnetometer". Physical Review D. 82 (11): 111901. arXiv:1011.2143. Bibcode:2010PhRvD..82k1901G. doi:10.1103/PhysRevD.82.111901. S2CID 118438569.
  25. ^ M. Smiciklas; et al. (2011). "New Test of Local Lorentz Invariance Using a 21Ne-Rb-K Comagnetometer". Physical Review Letters. 107 (17): 171604. arXiv:1106.0738. Bibcode:2011PhRvL.107q1604S. doi:10.1103/PhysRevLett.107.171604. PMID 22107506. S2CID 17459575.
  26. ^ Peck, S.K.; et al. (2012). "New Limits on Local Lorentz Invariance in Mercury and Cesium". Physical Review A. 86 (1): 012109. arXiv:1205.5022. Bibcode:2012PhRvA..86a2109P. doi:10.1103/PhysRevA.86.012109. S2CID 118619087.
  27. ^ Hohensee, M.A.; et al. (2013). "Limits on violations of Lorentz symmetry and the Einstein equivalence principle using radio-frequency spectroscopy of atomic dysprosium". Physical Review Letters. 111 (5): 050401. arXiv:1303.2747. Bibcode:2013PhRvL.111e0401H. doi:10.1103/PhysRevLett.111.050401. PMID 23952369. S2CID 27090952.
  28. ^ Allmendinger, F.; et al. (2014). "New limit on Lorentz and CPT violating neutron spin interactions using a free precession 3He-129Xe co-magnetometer". Physical Review Letters. 112 (11): 110801. arXiv:1312.3225. Bibcode:2014PhRvL.112k0801A. doi:10.1103/PhysRevLett.112.110801. PMID 24702343. S2CID 8122573.

Read other articles:

العلاقات اليمنية الكمبودية

العلاقات اليمنية الكمبودية اليمن كمبوديا   اليمن   كمبوديا تعديل مصدري - تعديل   العلاقات اليمنية الكمبودية هي العلاقات الثنائية التي تجمع بين اليمن وكمبوديا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة الي�...

 

 

Realisme (hubungan internasional)

Il Principe karya Niccolò Machiavelli adalah perintis pemikiran realis Realisme adalah mazhab teori hubungan internasional. Realisme adalah spektrum ide[1] yang berpusat pada empat ide utama, yaitu grupisme politik, egoisme, anarki internasional, dan politik kekuasaan.[2] Teori realisme politik berawal dari tulisan-tulisan Thomas Hobbes dan Niccolò Machiavelli, kemudian muncul sebagai pendekatan berbasis hubungan internasional pada masa selang antara Perang Dunia I dan Peran...

 

 

Čakanovce, Košice-okolie District

Municipality of Slovakia Košice-okolie District in the Košice Region Čakanovce (Hungarian: Ósvacsákány) is a village and municipality in Košice-okolie District in the Košice Region of eastern Slovakia. History In historical records, the village was first mentioned in 1439. Geography The village lies at an altitude of 240 metres and covers an area of 9.617 km2. It has a population of about 556 people. Genealogical resources The records for genealogical research are available at th...

Wend von Wietersheim

German general (1900–1975) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Wend von Wietersheim – news · newspapers · books · scholar · JSTOR (October 2016) (Learn how and when to remove this template message)Wend von WietersheimBorn(1900-04-18)18 April 1900Neuland, SilesiaDied19 September 1975(1975-09-19)...

 

 

Jane Goodall

Untuk pengarang asal Australia, lihat Jane R. Goodall. DameJane GoodallDBEGoodall di Tanzania tahun 2018LahirValerie Jane Morris-Goodall3 April 1934 (umur 90)London, Inggris, Britania RayaAlmamaterNewnham College, CambridgeDarwin College, CambridgeDikenal atasPenelitian simpanse, pelestarian, kesejahteraan hewanSuami/istriHugo van Lawick ​ ​(m. 1964; cer 1974)​ Derek Bryceson ​ ​(m. 1975; meninggal 1980...

 

 

Æthelberht of Kent

King of Kent (589–616) ÆthelberhtStatue of ÆthelberhtInterior of Rochester CathedralKing of KentReignc. 589 – 616PredecessorEormenricSuccessorEadbaldBornc. 550Died24 February 616(616-00-00) (aged 65–66)BurialSt Augustine's AbbeyConsortBertha of Kent[1]IssueEadbaldÆthelburgÆðelwaldHouseKentFatherEormenricReligionChristianity prev. Anglo-Saxon paganism Æthelberht (/ˈæθəlbərt/; also Æthelbert, Aethelberht, Aethelbert or Ethelbert; Old English: Æðelberht [...

Marri Chenna Reddy

Indian politician (1919–1996) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Marri Chenna Reddy – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and when to remove this message) Marri Chenna ReddyOfficial portrait of Chenna Reddy12th Governor of Tamil NaduIn office31 May 1993&...

 

 

Tongan literature

Part of a series on theCulture of Tonga History Timeline Early empire Kingdom of Tonga (1900–1970) Muʻa Tuʻi Tonga Tuʻi Haʻatakalaua Tuʻi Kanokupolu 2006 Nukuʻalofa riots Cyclone Gita COVID-19 pandemic 2022 Hunga Tonga–Hunga Haʻapai eruption and tsunami People Languages Cuisine Religion Literature Music Sport Monuments Symbols Flag Coat of arms National anthem vte Among the first published works of Tongan literature, in the late 1960s and early 1970s, were 'Epeli Hau'ofa's short st...

 

 

Utah

U.S. state This article is about the U.S. state. For other uses, see Utah (disambiguation). State in the United StatesUtah Áshįįh Biiʼtó Hahoodzocode: nav promoted to code: nv  (Navajo)State FlagSealNicknames: Beehive State (official), The Mormon State, DeseretMotto: IndustryAnthem: Utah...This Is the PlaceMap of the United States with Utah highlightedCountryUnited StatesBefore statehoodUtah TerritoryAdmitted to the UnionJanuary 4, 1896 (45th)Capital(and largest city)Salt ...

Werkzeug

Erfolgsmodell über Jahrtausende: der Faustkeil Stillleben mit Nähutensilien, Wilhelm Wittmann, 1889 Ein Werkzeug ist ein nicht zum Körper eines lebenden oder künstlichen Organismus gehörendes Objekt, mit dessen Hilfe die Funktionen des Körpers erweitert werden, um auf diese Weise ein unmittelbares Ziel zu erreichen.[1] Dieses Ziel ist in Handwerk und Industrie die Veränderung eines Werkstücks. Eine Sammlung verschiedener Werkzeuge, die nötig für eine bestimmte Tätigkeit sin...

 

 

Church of the Holy Equal-to-the-Apostles Prince Vladimir of Makhachkala

Church in Dagestan, RussiaChurch of the Holy Equal-to-the-Apostles Prince VladimirХрам Святого Равноапостольного Князя Владимира (Russian)Church of the Holy Equal-to-the-Apostles Prince Vladimir in Makhachkala42°59′03″N 47°30′16″E / 42.98417°N 47.50444°E / 42.98417; 47.50444LocationMakhachkala, DagestanCountryRussiaDenominationEastern OrthodoxyHistoryStatusActiveConsecratedMay 7, 2016ArchitectureStyleDagestan a...

 

 

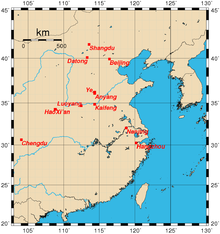
Ye (Chine)

Pour les articles homonymes, voir Yè. Cet article est une ébauche concernant une localité chinoise. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Carte interactive de Ye ancienne carte représentant Ye Ye (Chinois: 鄴 ; pinyin : Yè), également connue sous les noms de Yejun ou de Jizhou, était une ville de Chine ancienne située dans la province de Ji. Aujourd'hui son site archéologique se sit...

Glendale, Colorado

City in Colorado, United States This article is about the city in Arapahoe County, Colorado. For the census-designated place in Boulder County, see Glendale, Boulder County, Colorado. For 19th-century settlement, see Glendale, Colorado Territory. Home rule municipality in Colorado, United StatesGlendale, ColoradoHome rule municipality[1]City of Glendale[1]The City of Glendale Municipal Center SealMotto: The Heartbeat of Metro DenverLocation of the City of Glendale in Arap...

 

 

Daftar lagu posisi pertama Billboard tahun 1944

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber...

 

 

Wangsa Howard

Wangsa HowardLambang Howard, diberikan oleh Thomas HowardNegaraKerajaan Inggris, Britania RayaKelompok etnisInggris (lihat keterangan)Didirikan1483PendiriJohn HowardKepala saat iniEdward Fitzalan-HowardGelar See list Extant Titles Adipati Norfolk Kardinal Pelindung Inggris Earl Arundel Earl Surrey Earl Norfolk Earl Effingham Earl Nottingham Earl Berkshire Earl Norwich FitzAlan dari Derwent Baron Stafford Baron Lanerton Baron Furnivall Baron Howard Earl Norwich Earl Berkshire Earl Effingham Ho...

Cellule de Kupffer

Vaisseaux sinusoïdes de foie (de rat), entretenus par les cellules de Küpfer ; on aperçoit ici les cellules endothéliales fenêtrées (percées de trous) qui permettent au foie de jouer son rôle de détoxication de l'organisme. structure typique du foie Les cellules de Kupffer sont les macrophages[1] résidants appartenant au groupe des macrophages hépatiques et notamment au lobule hépatique où elles sont très nombreuses (jusqu'à environ 30 % de toutes les cellules hépati...

 

 

Nio (automobile)

Pour les articles homonymes, voir NIO. Nio Création 2014 Fondateurs William Li Forme juridique Company limited by shares (d)[1] Action New York Stock Exchange (NIO) et bourse de Hong Kong (9866)[2] Siège social Shanghai Chine Direction William Li (en) Actionnaires Tencent HoldingsBaidu[3]Hillhouse Capital GroupSequoia Capital Activité Construction automobile Produits Voiture électrique Filiales Nio Formula E Team NextEV Site web https://www.nio.io/ modifier - modifier le code - voir...

 

 

In Darkness (2011 film)

2011 film In DarknessUK cinematic posterDirected byAgnieszka HollandWritten byDavid F. ShamoonBased onIn the Sewers of Lvovby Robert MarshallProduced byAndrzej Besztak Steffen Reuter Patrick Knippel Marc-Daniel Dichant Leander Carell Juliusz Machulski Paul Stephens Eric JordanStarringRobert Więckiewicz Benno Fürmann Agnieszka GrochowskaMaria Schrader Herbert Knaup Kinga Preis Krzysztof SkoniecznyCinematographyJolanta DylewskaEdited byMike CzarneckiMusic byAntoni Komasa-ŁazarkiewiczProducti...

Garden square

Communal garden surrounded by buildings Bloomsbury Square, a garden square in central London, England A garden square is a type of communal garden in an urban area wholly or substantially surrounded by buildings; commonly, it continues to be applied to public and private parks formed after such a garden becomes accessible to the public at large. The archetypal garden square is surrounded by tall terraced houses and other types of townhouse. Because it is designed for the amenity of surroundin...

 

 

Jamshedpur

Metropolis City in Jharkhand, India Metropolis in Jharkhand, IndiaJamshedpur TatanagarMetropolisFrom top to bottom: TCE Building, Sakchi view (L), Tata Steel Zoology Park (R),Golmuri Golf Course,JRD Tata Sports ComplexNickname(s): 'Steel City of India', 'Pittsburgh of India'JamshedpurLocation of Jamshedpur in JharkhandShow map of JharkhandJamshedpurJamshedpur (India)Show map of IndiaCoordinates: 22°47′33″N 86°11′03″E / 22.79250°N 86.18417°E / 22.79250;...